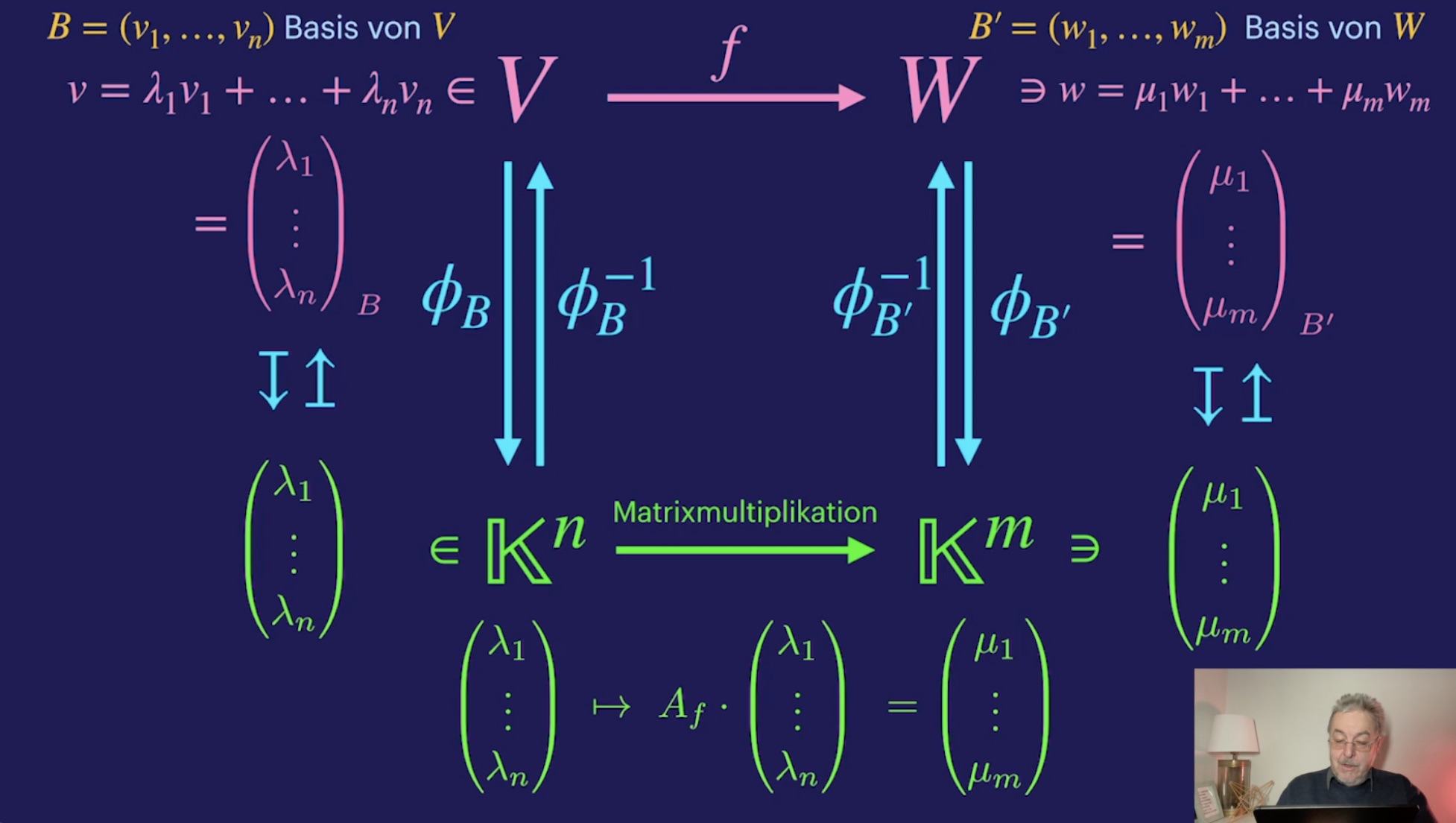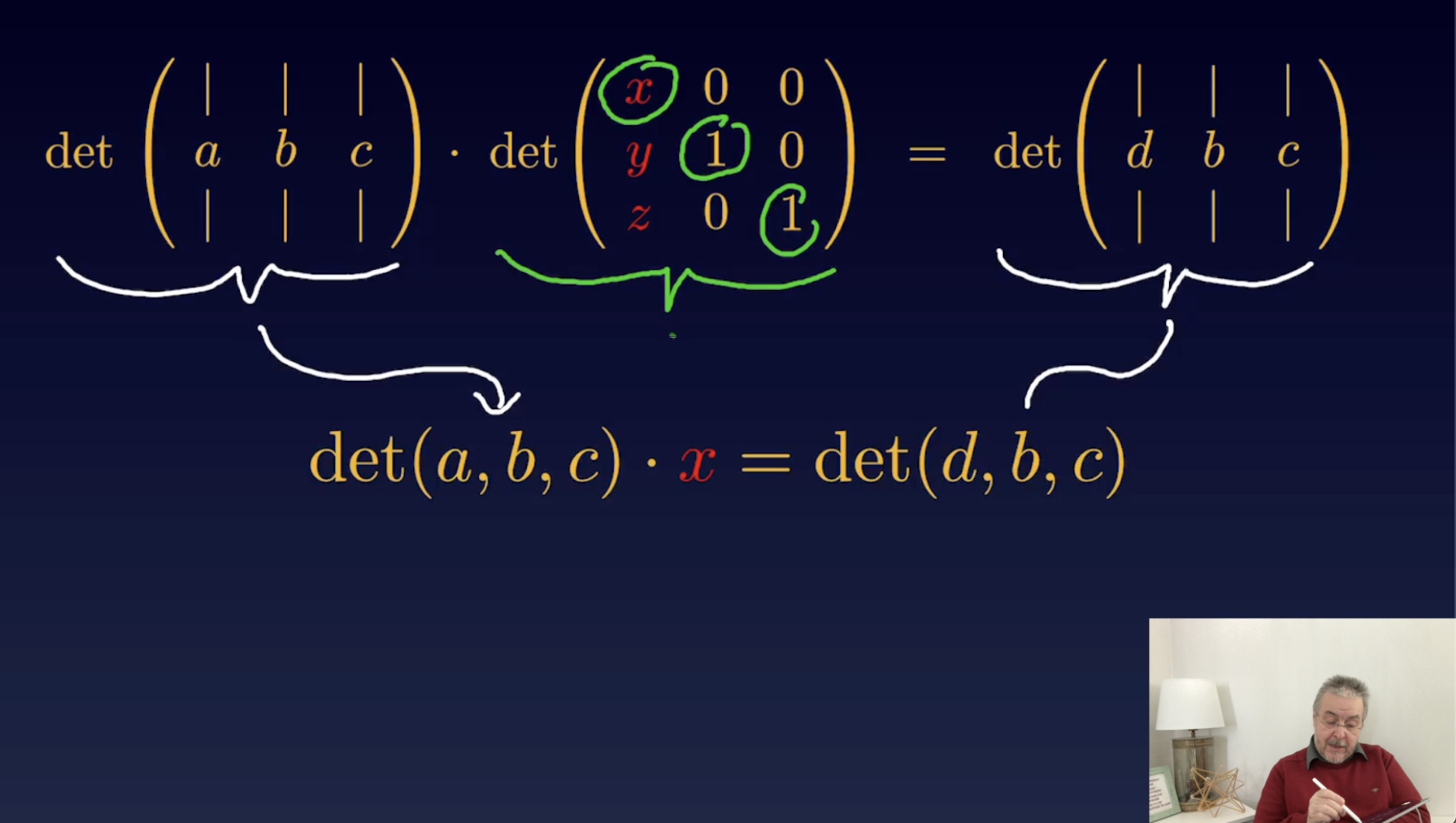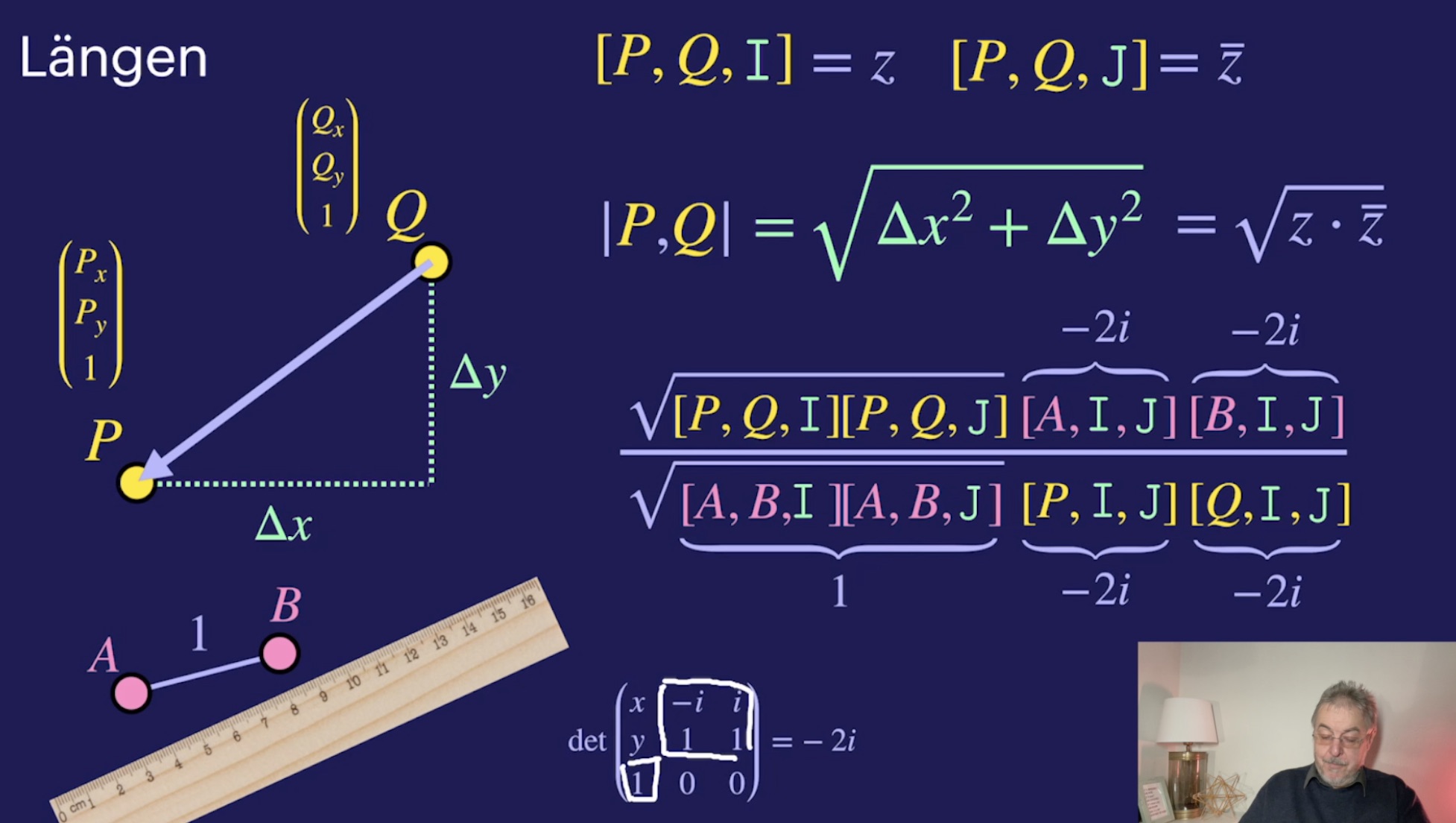My lectures
Lineare Algebra 1


Einleitung (33:18)
Einführende Beispiele (47:21)
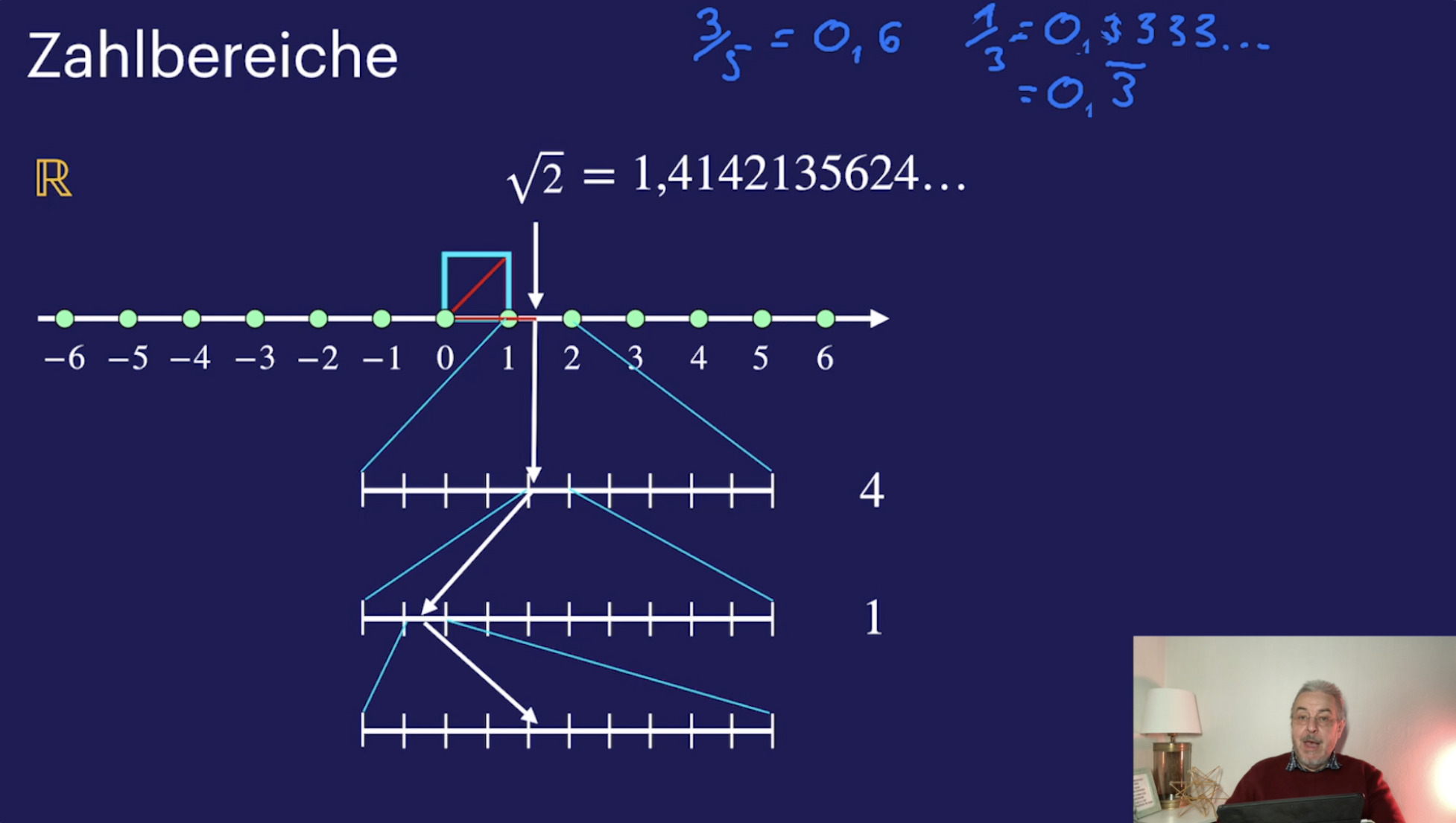
Zahlen, Mengen, Notationen (40:06)
Definition von Gruppen (31:05)

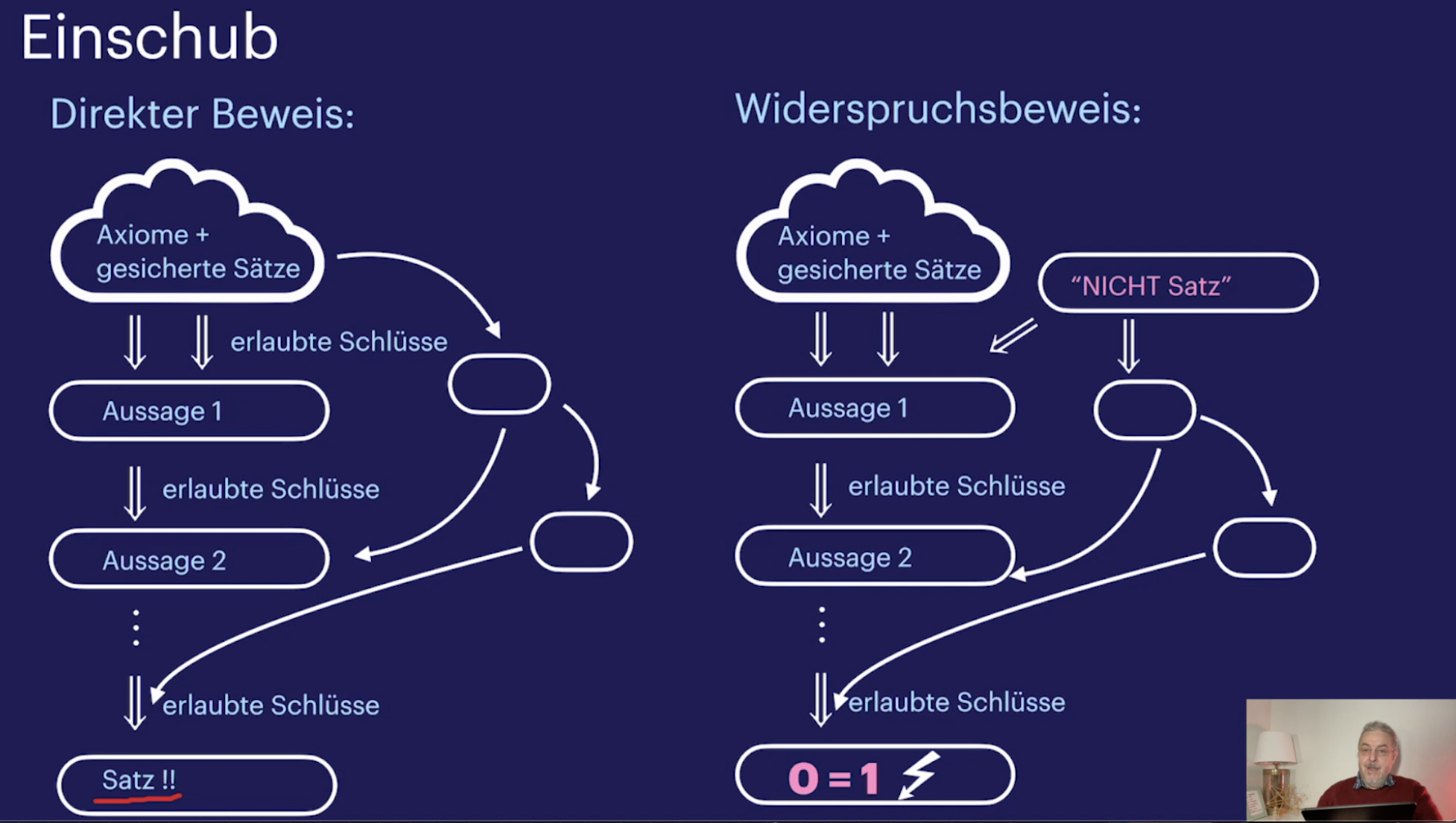
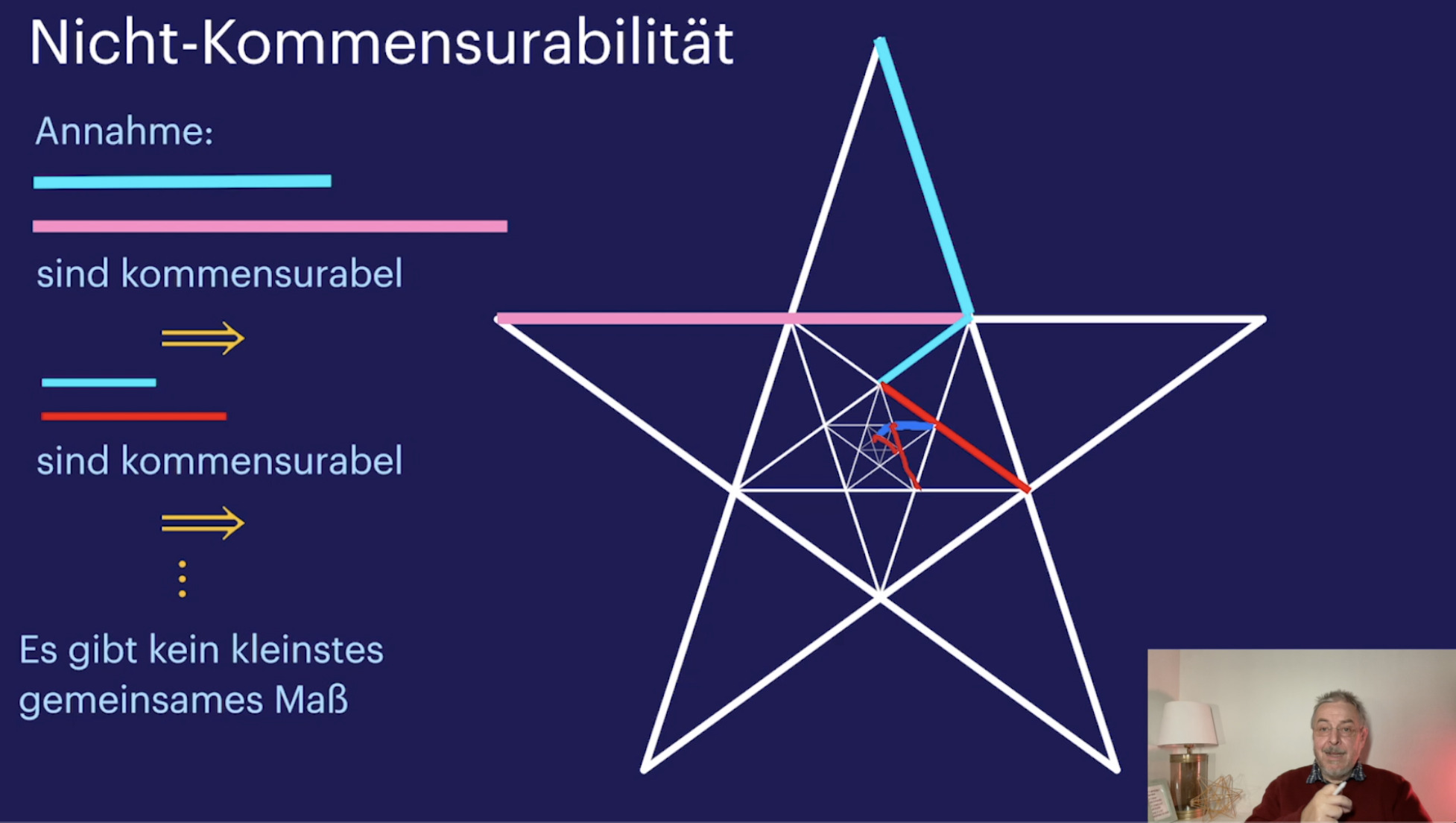
Einfache Sätze zu Gruppen (37:59)
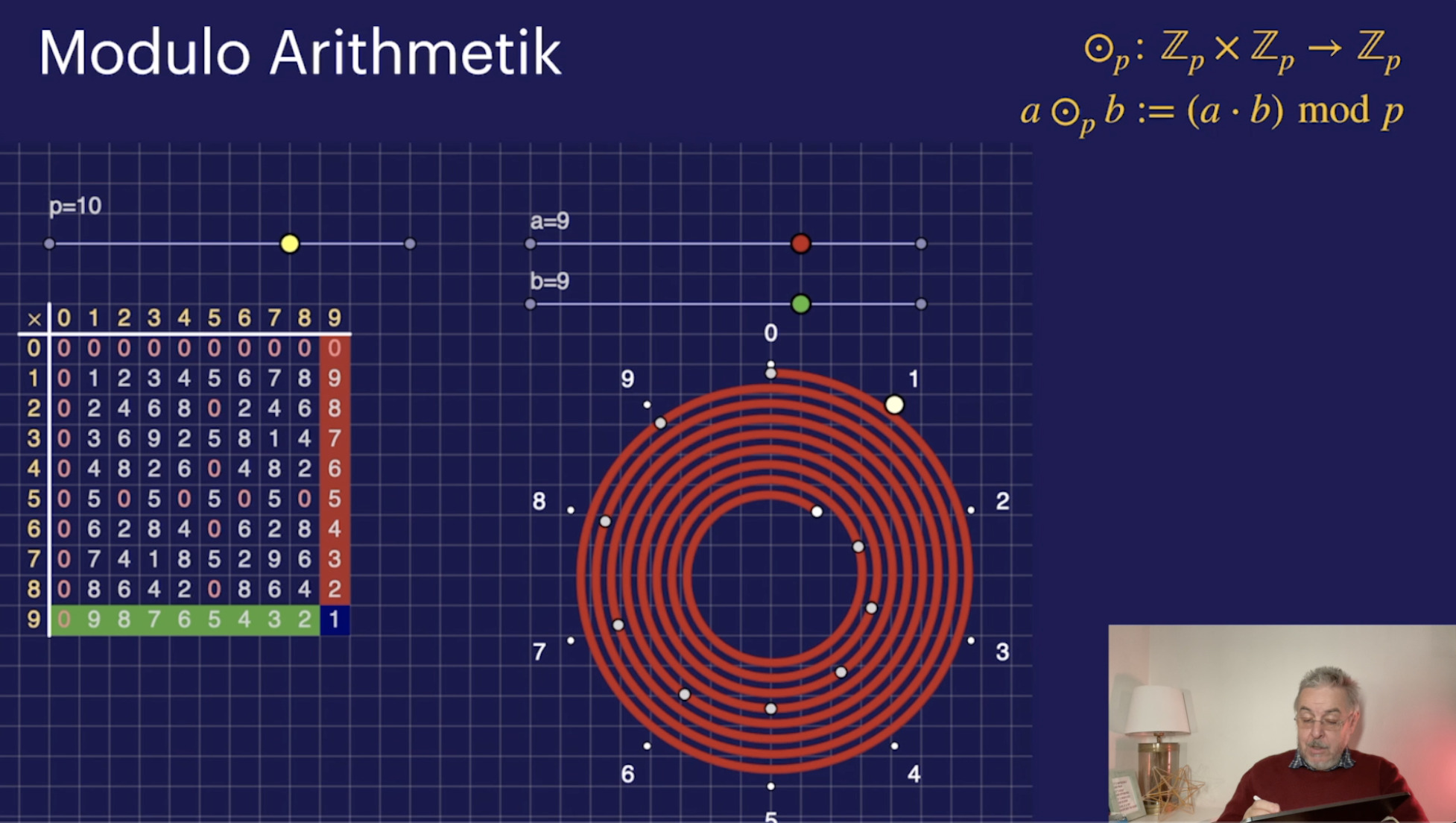
Modulo Arithmetik (21:55)
Modulo Arithmetik, Multiplikative Inverse (41:35)
Euklidischer Algorithmus (1:10:40)

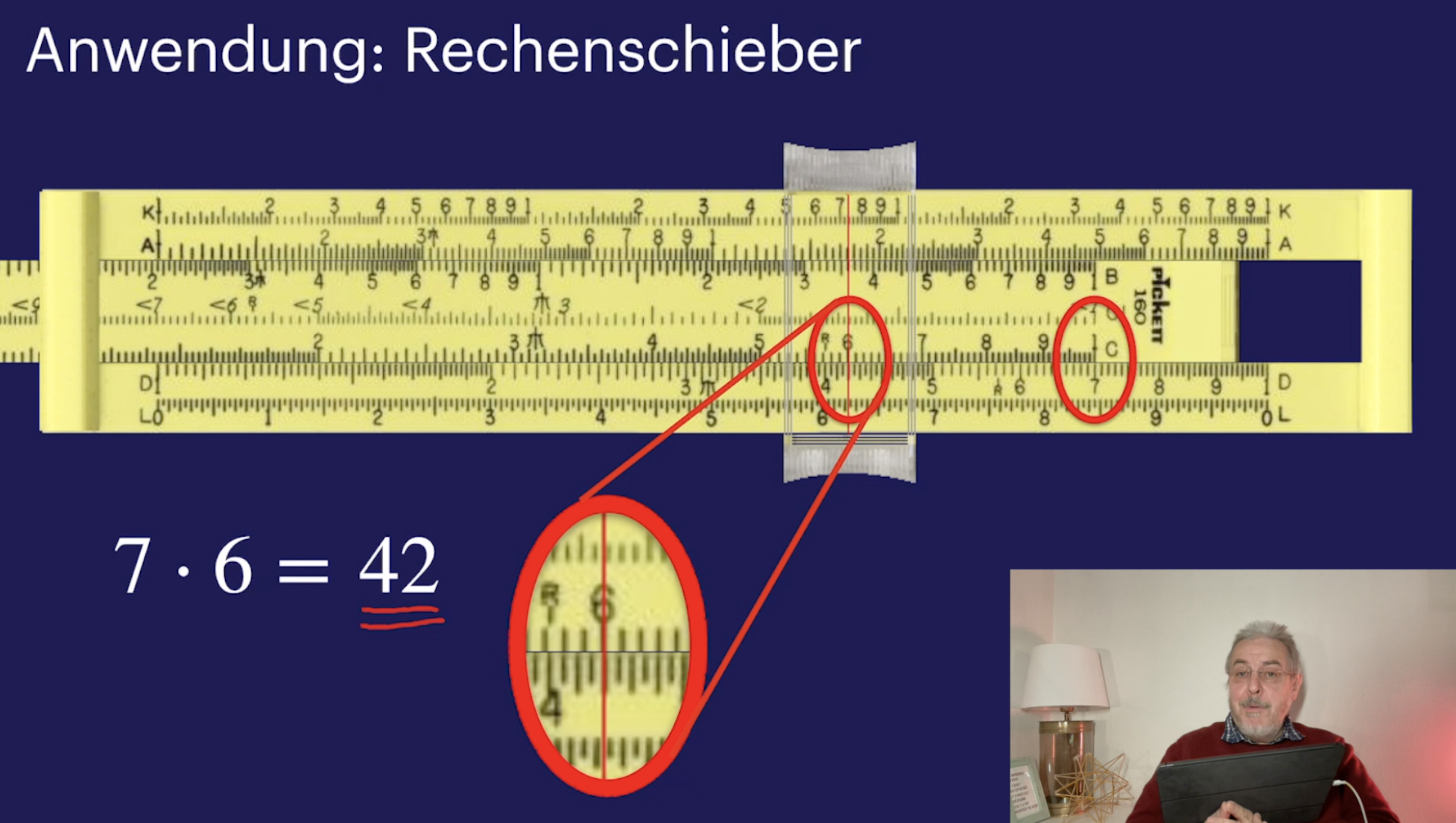
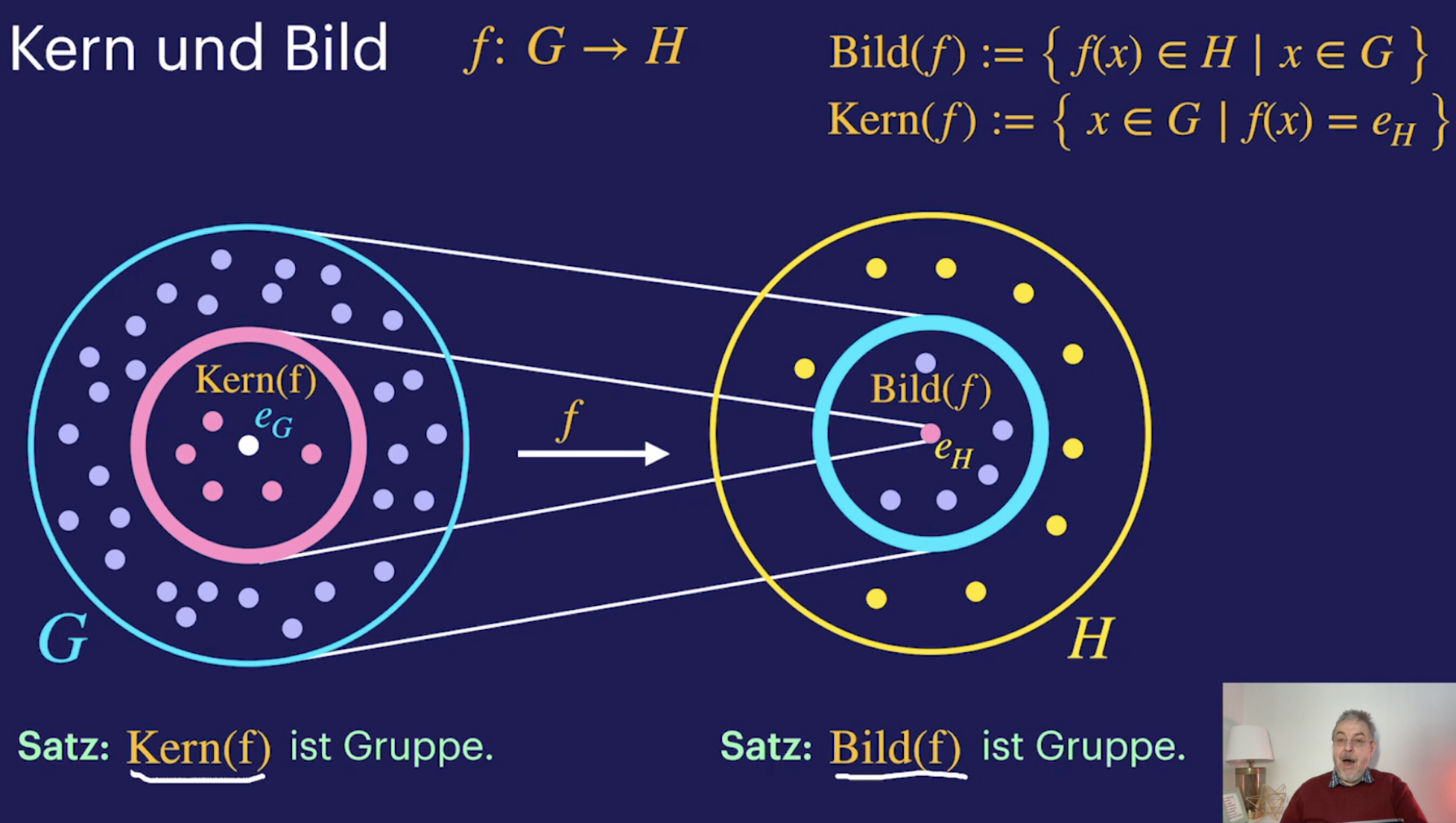

Untergruppen (28:28)
Homomorphismen (33:35)
Kern und Bild (32:00)
Relationen (34:15)
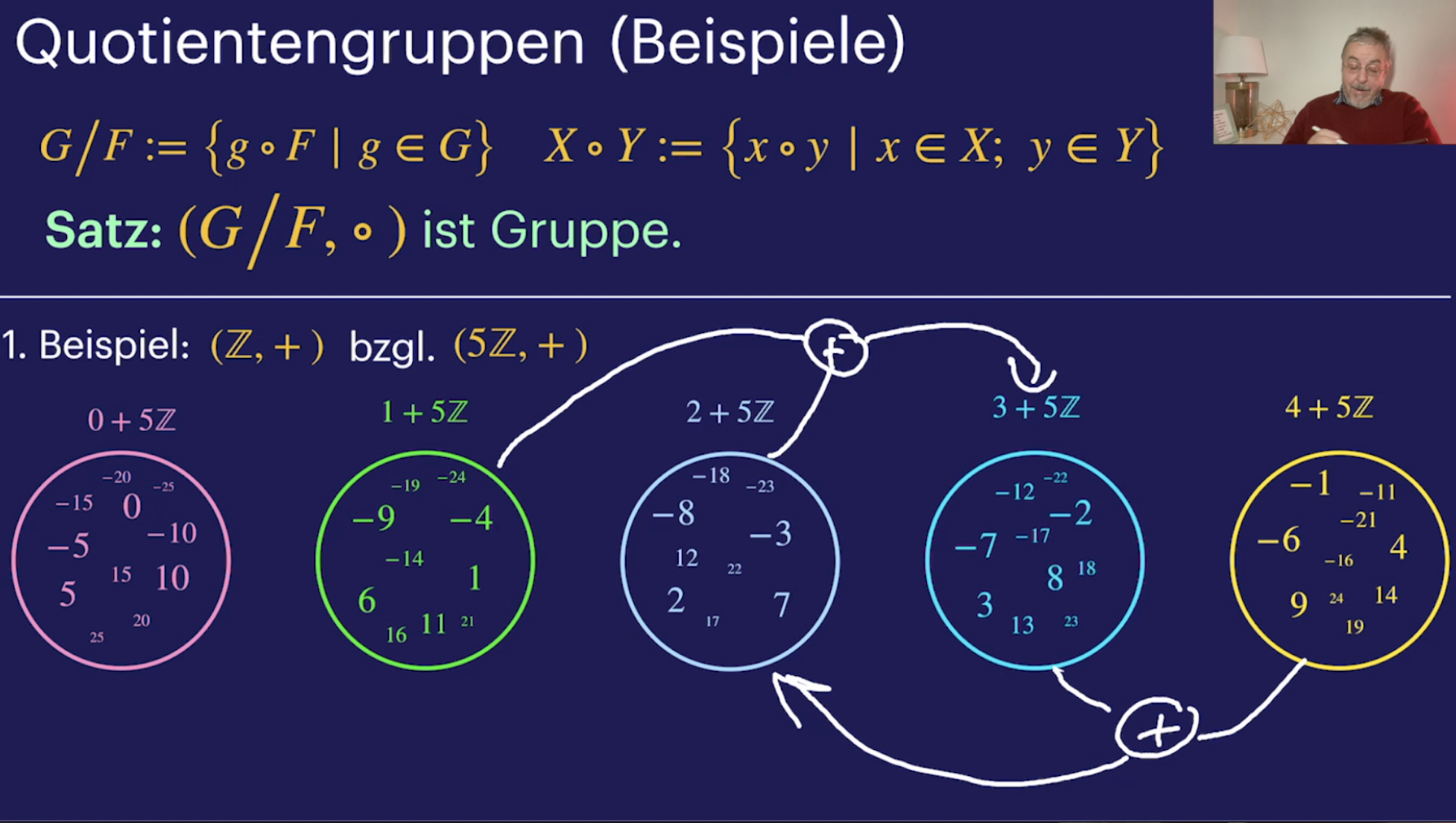
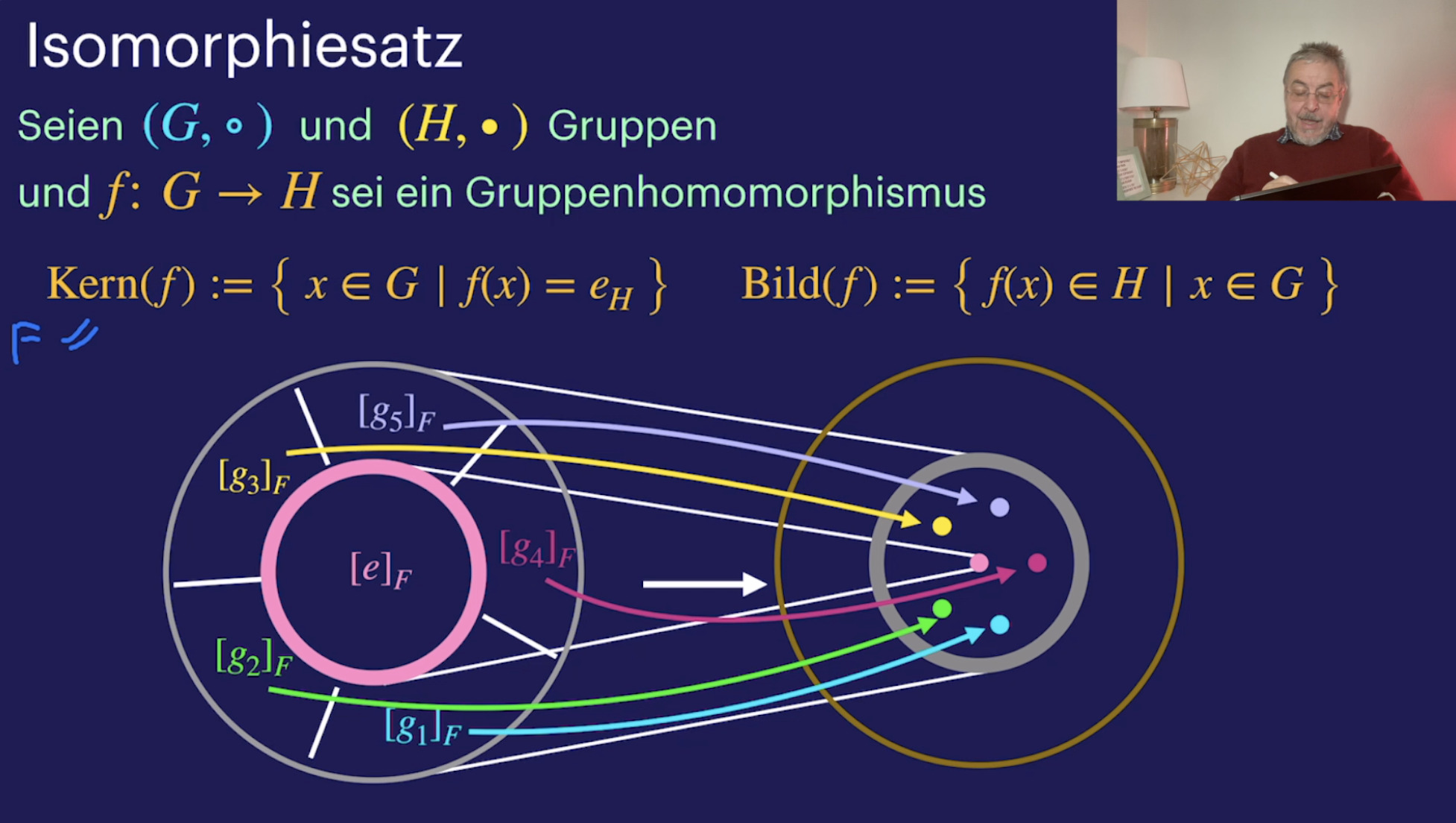

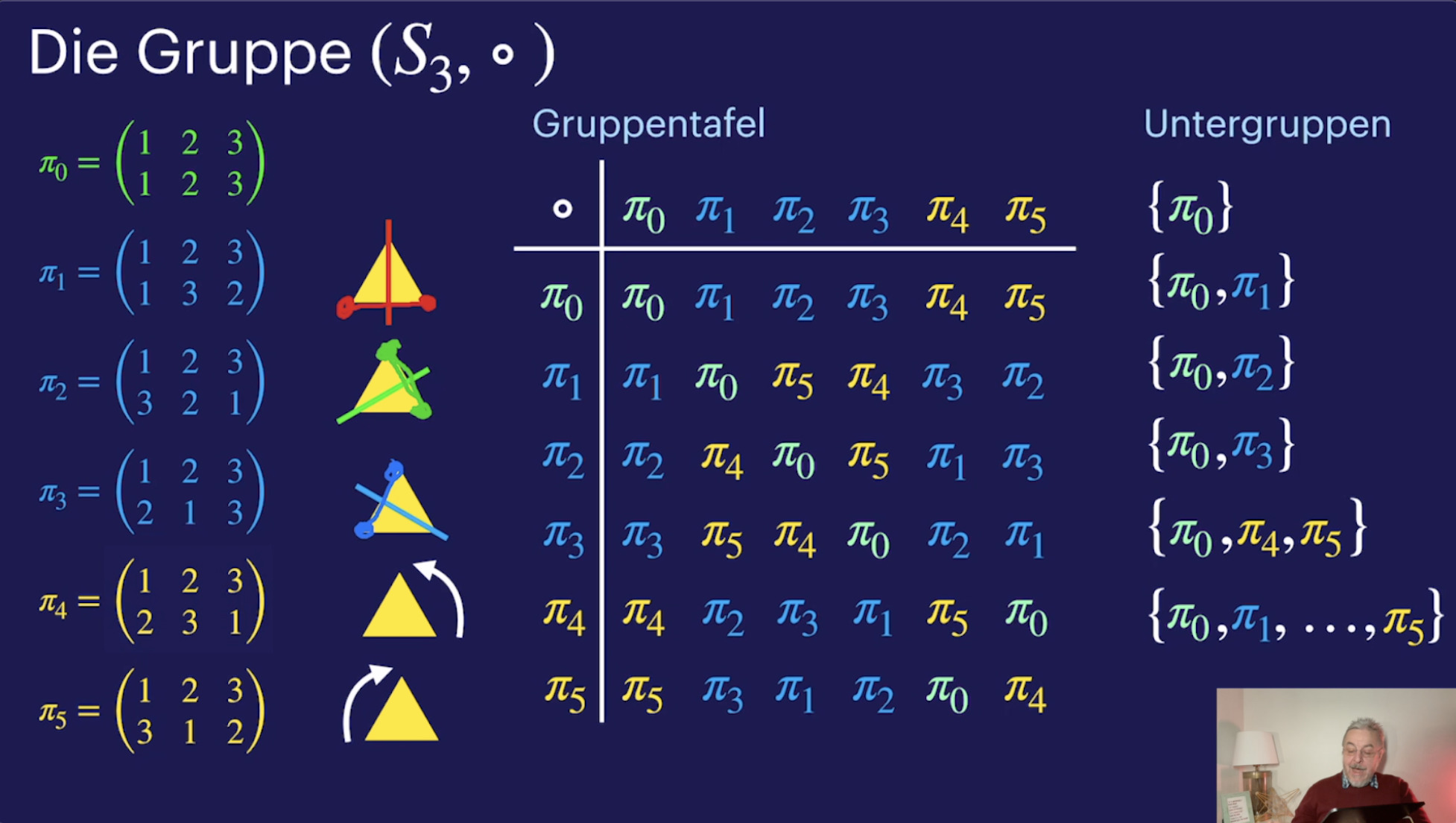
Quotientengruppen (1:07:17)
Isomorphiesatz (27:58)
Permutationen (23:59)
Die S_n als Gruppe (33:12)
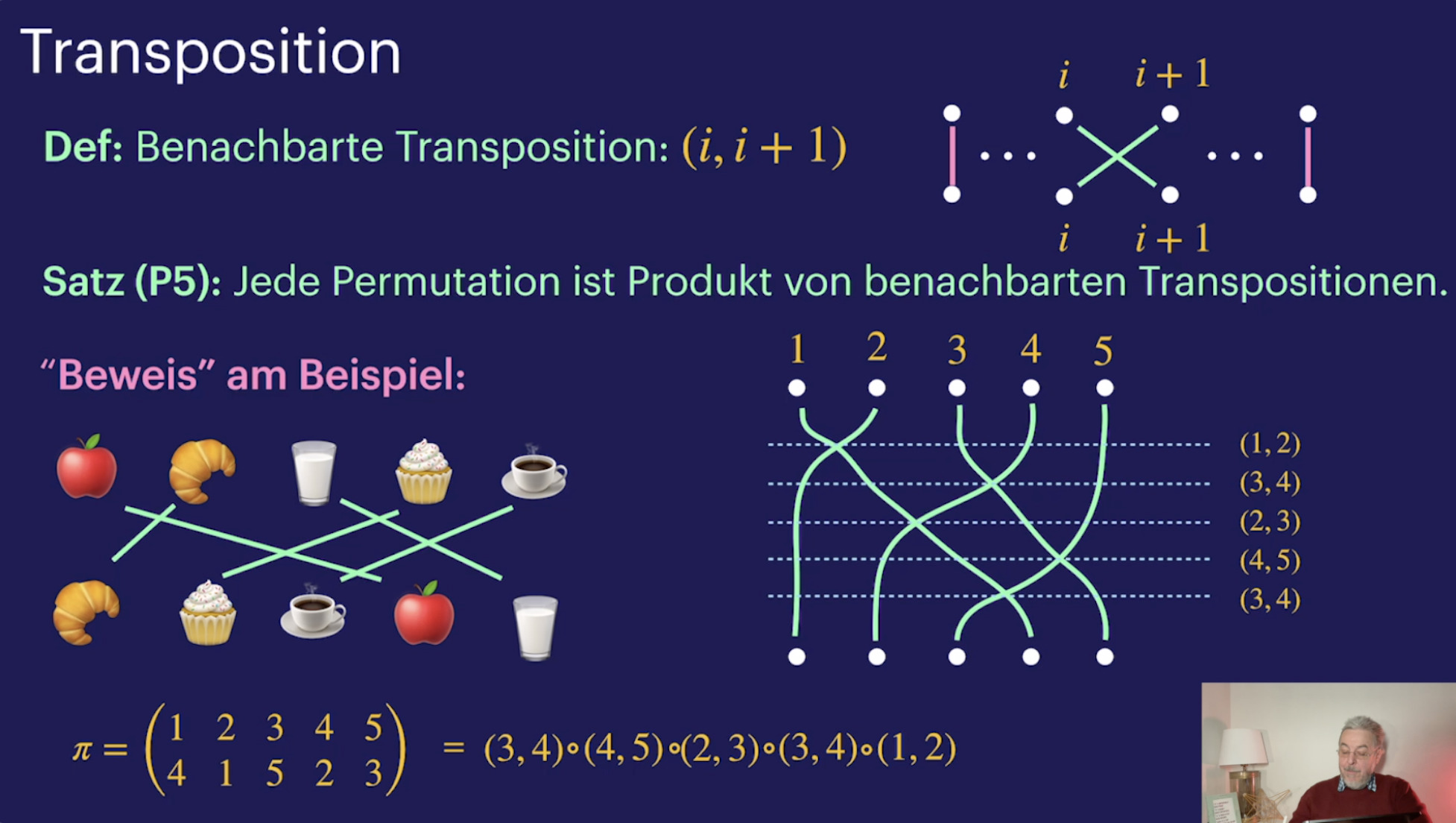



Zykel und Transpositionen (22:23)
Vorzeichen einer Permutation (30:45)
Ringe Körper (36:58)
Komplexe Zahlen (31:25)
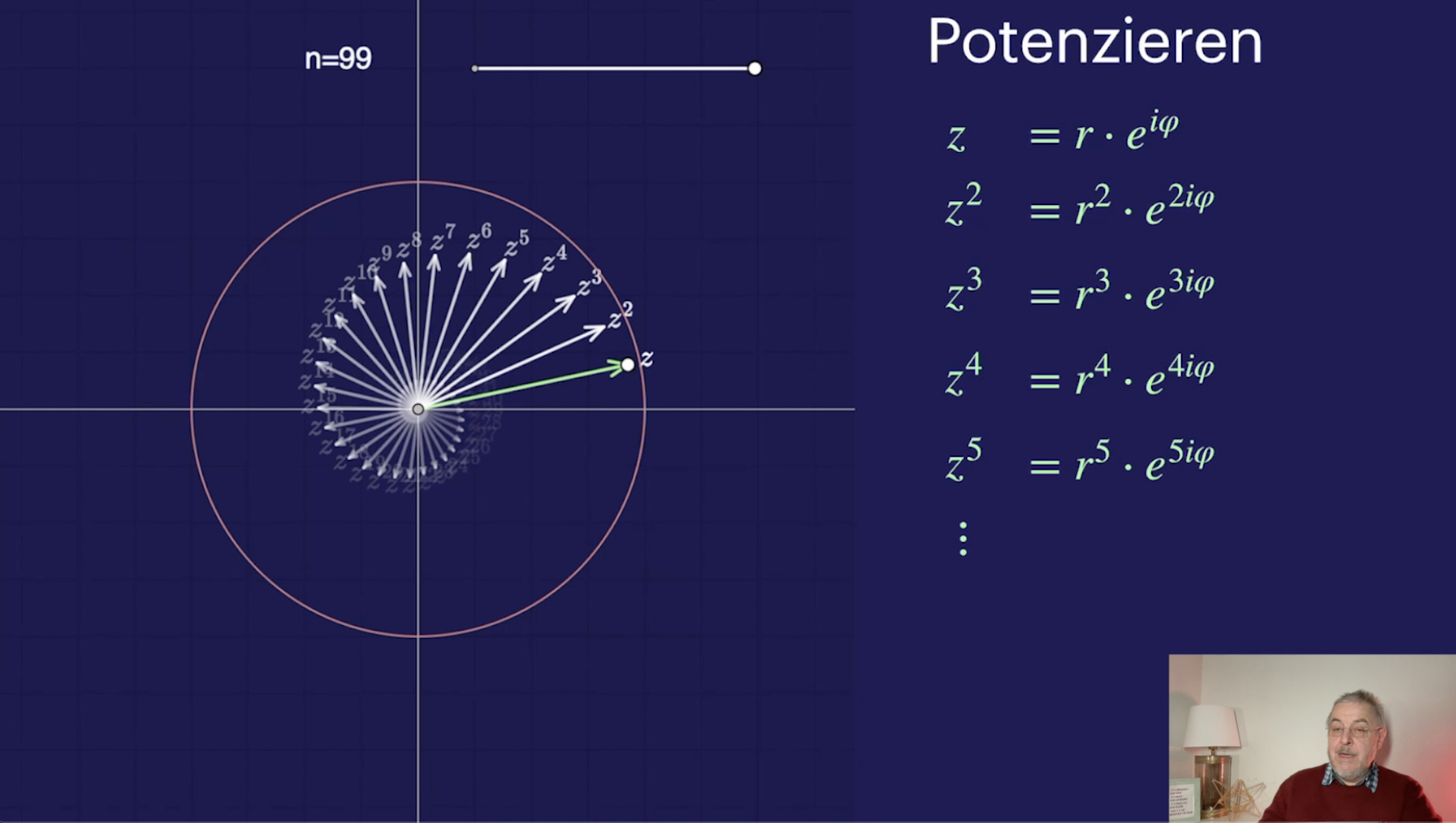
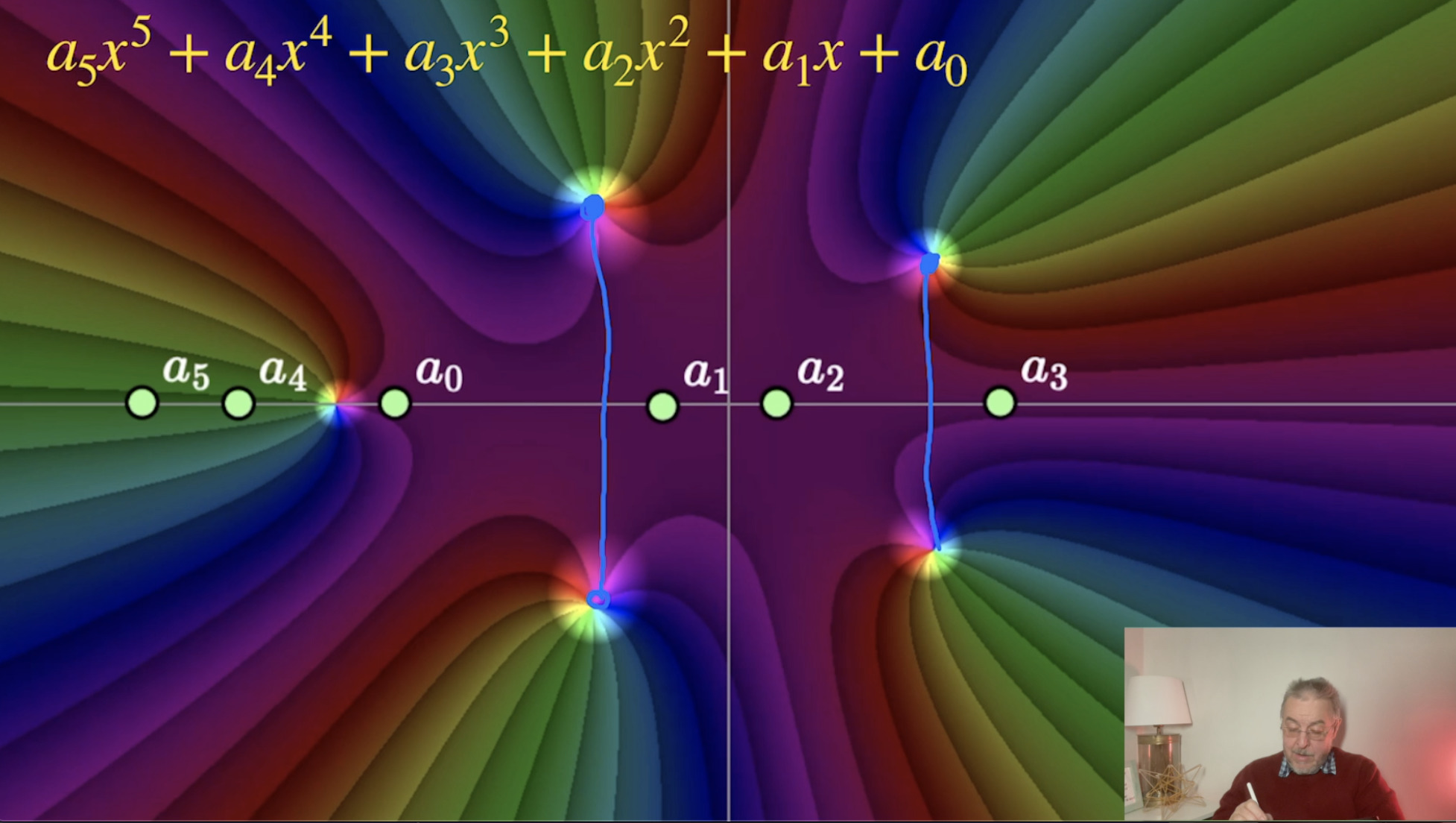
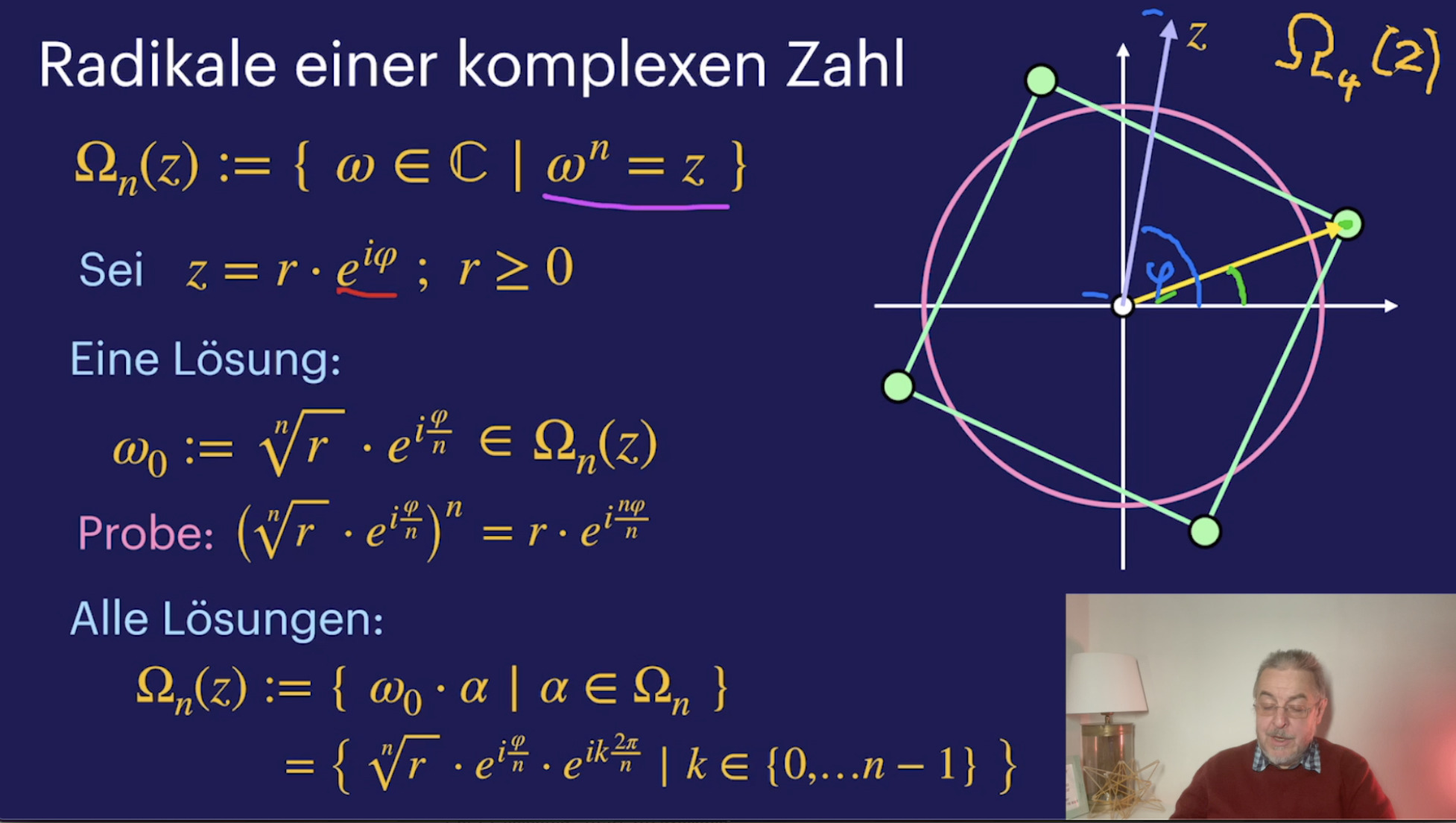
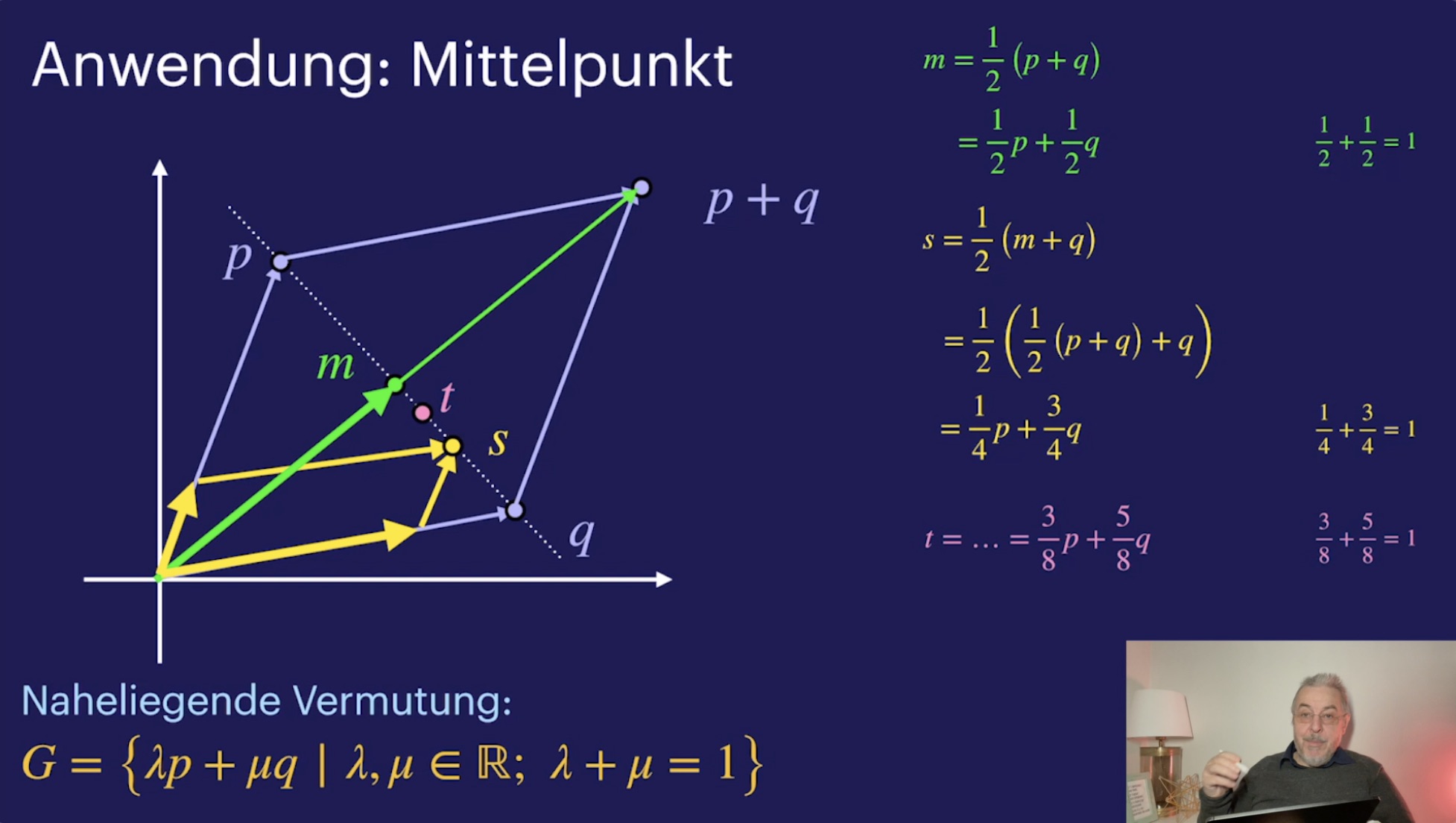
Geometrie komplexer Zahlen (43:37)
Fundamentalsatz der Algebra (54:36)
Einheitswurzeln (29:39)
Vektorraumaxiome (32:37)


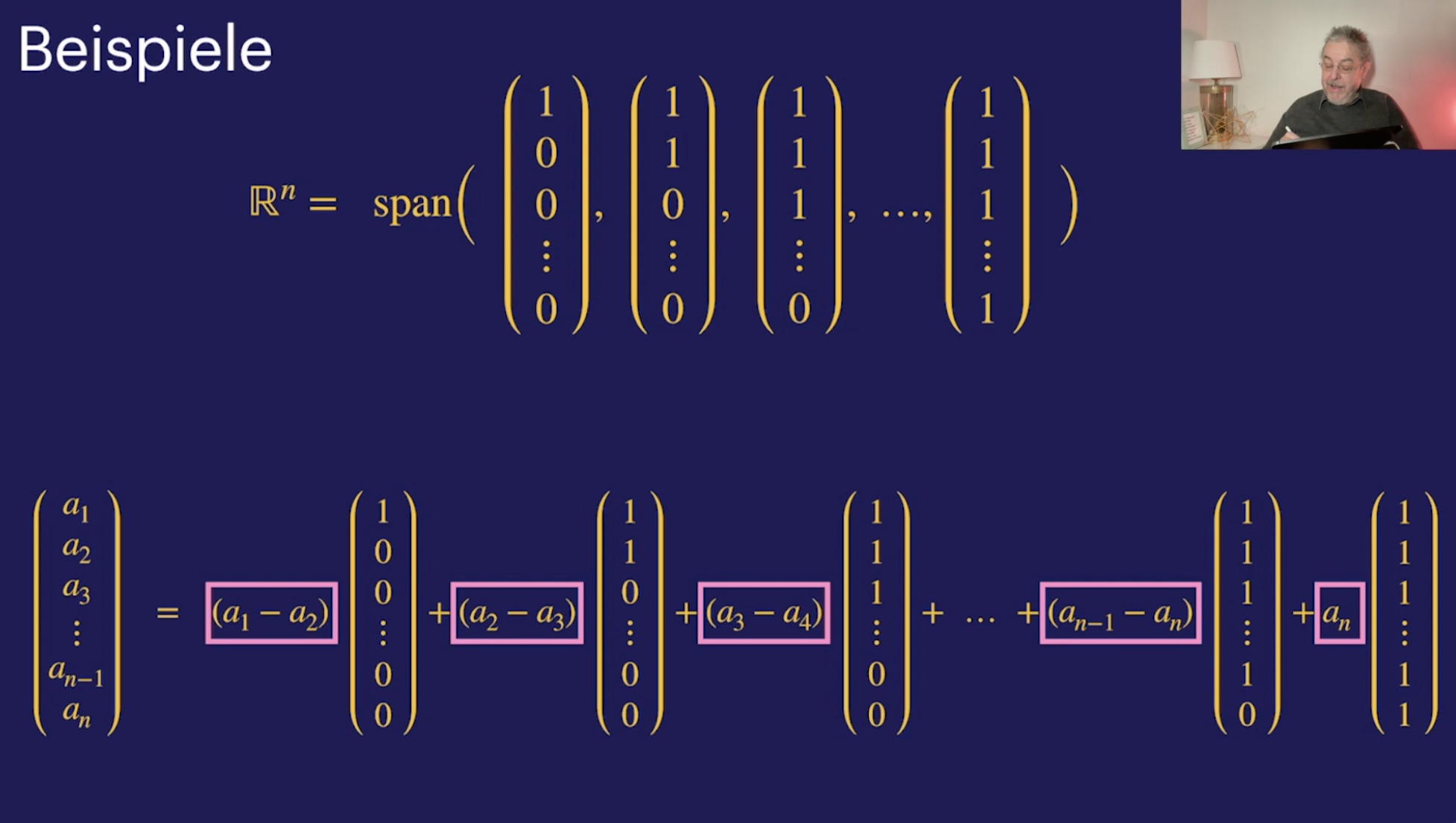

Grober Überblick (12:48)
Unterverktorräume (31:09)
Span (22:03)
Lineare Abhängigkeit (34:14)

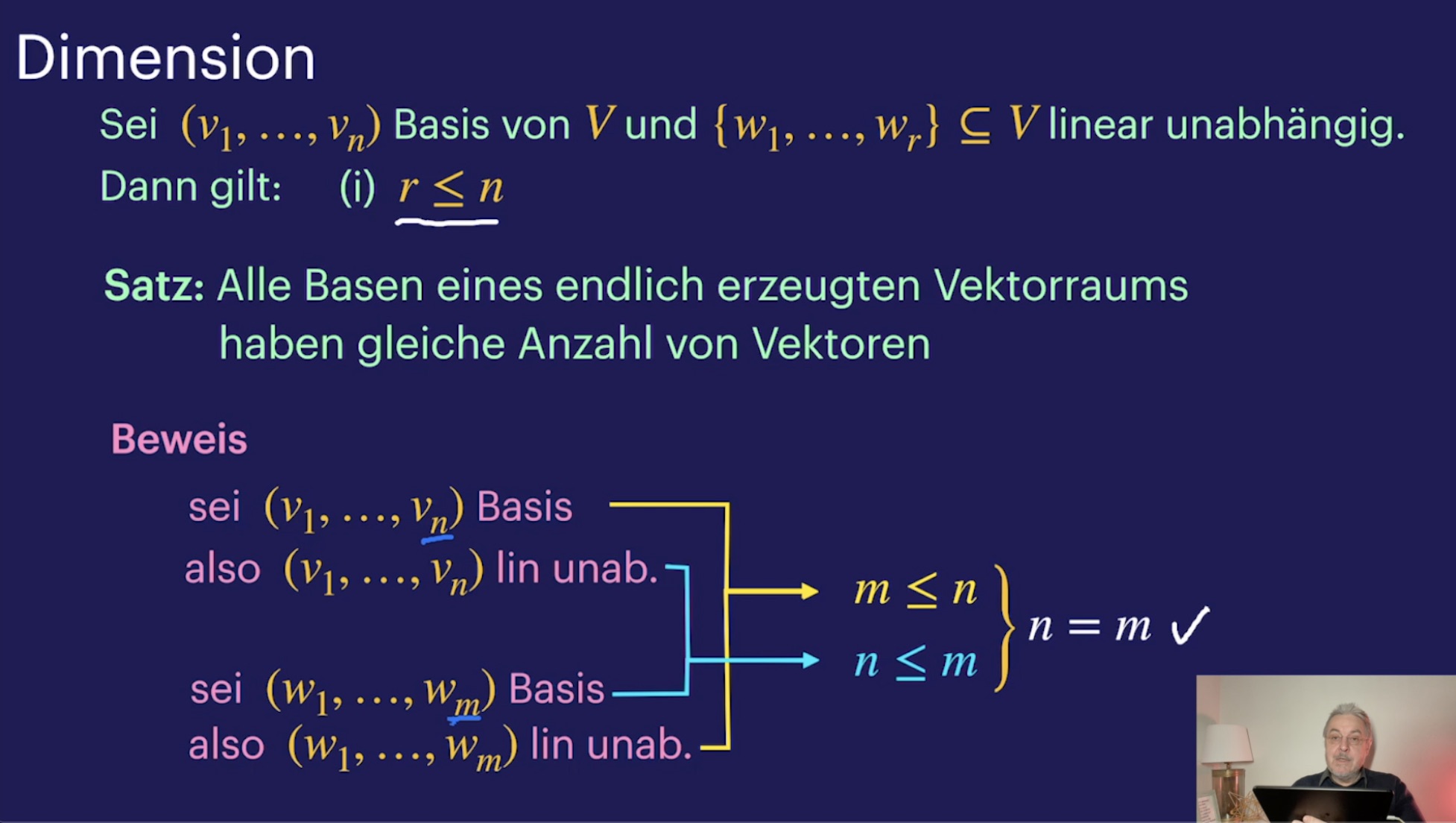
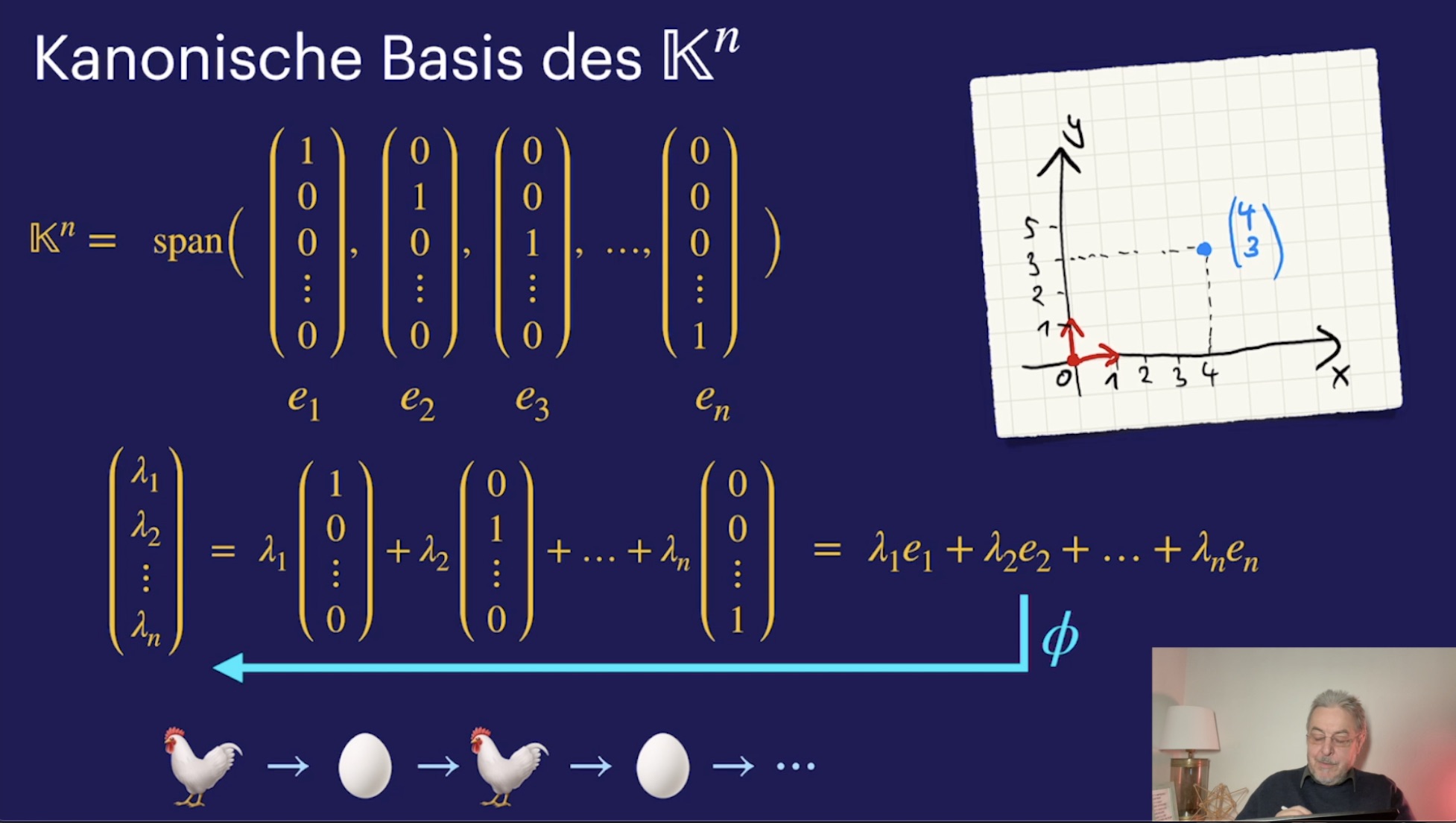

Basen (41:34)
Austauschsatz und Dimension (50:42)
Von Basen zu Koordinaten (50:42)
Lineare Abbildungen als Transformationen(37:27)

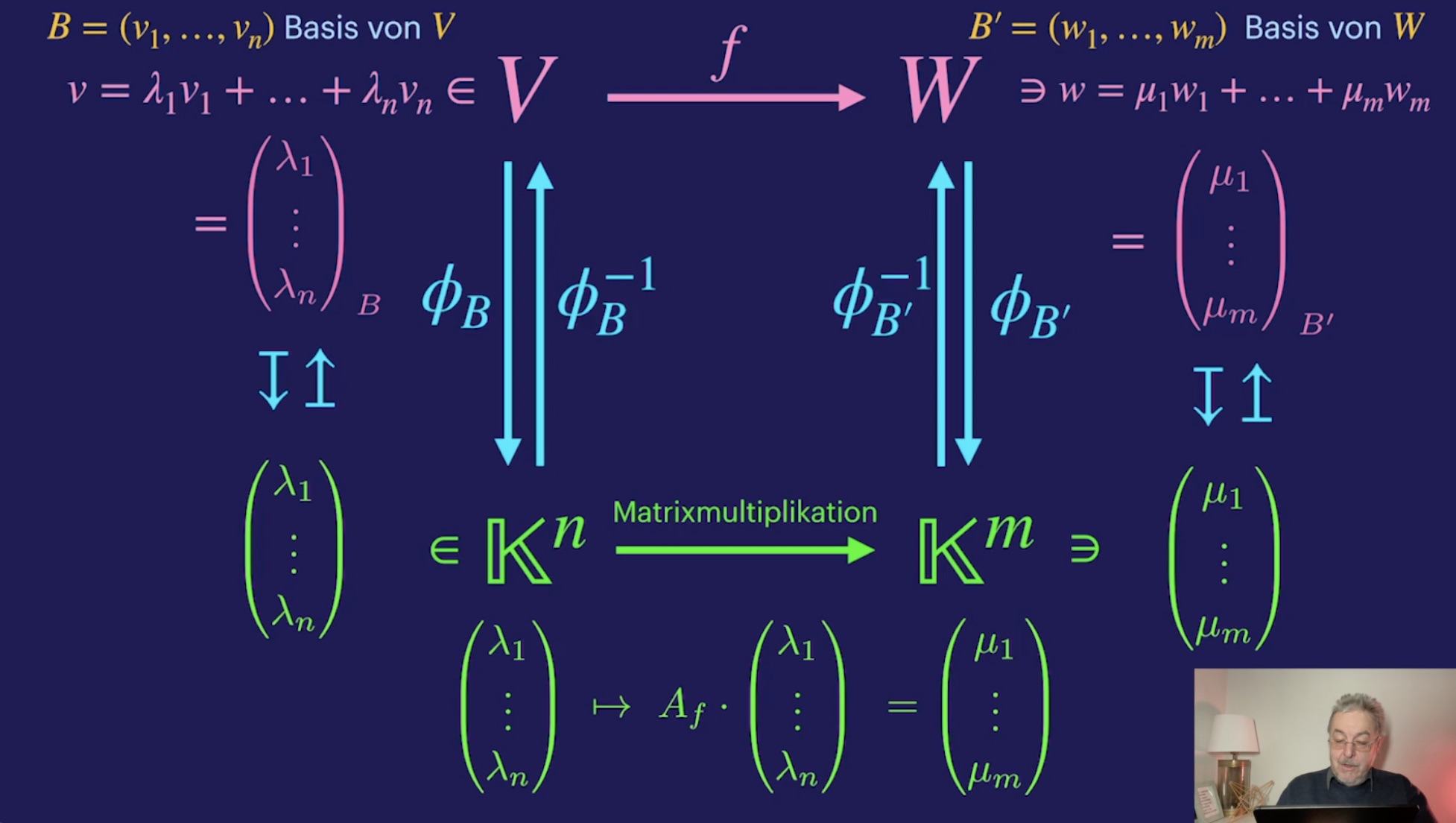
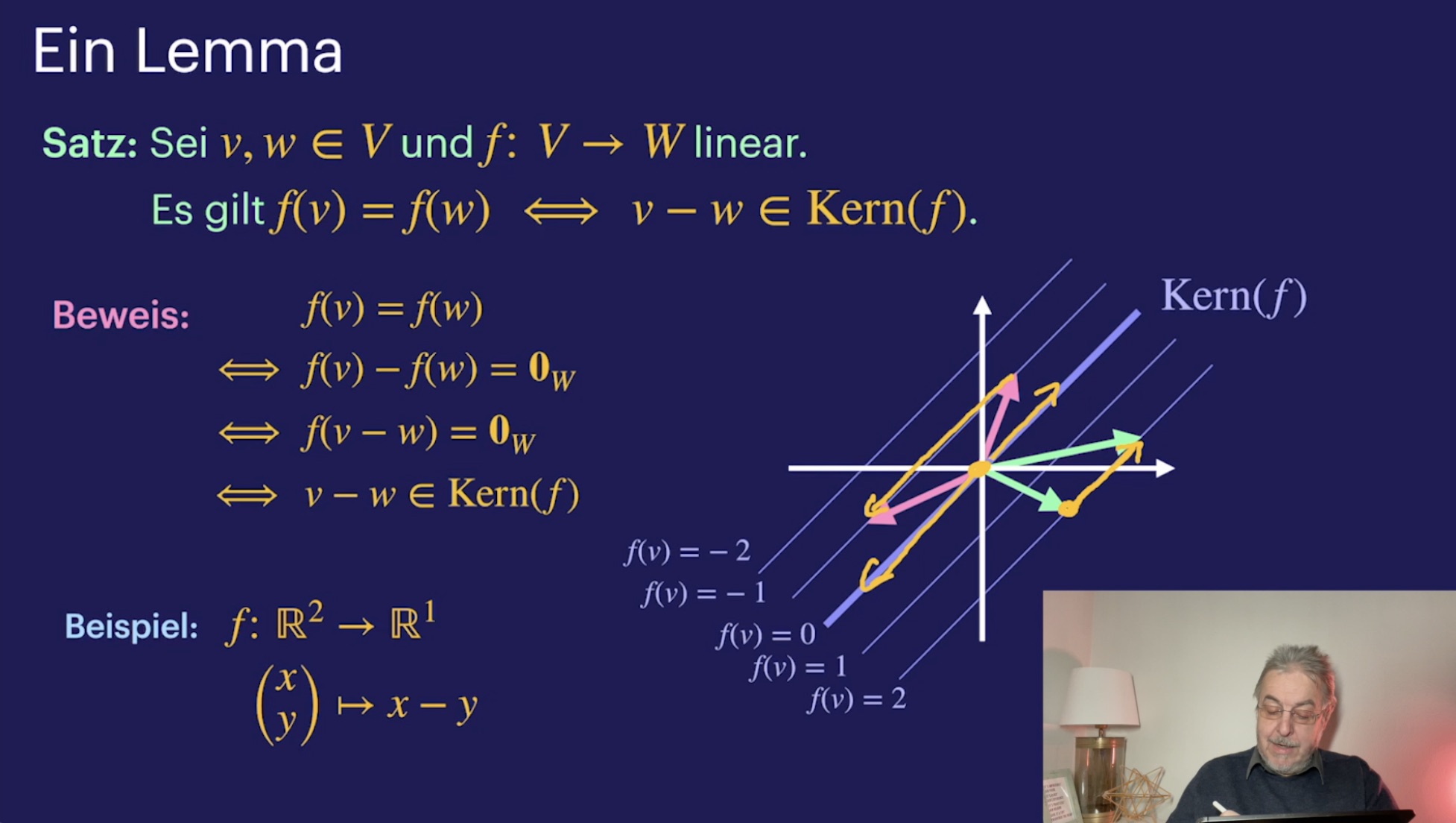
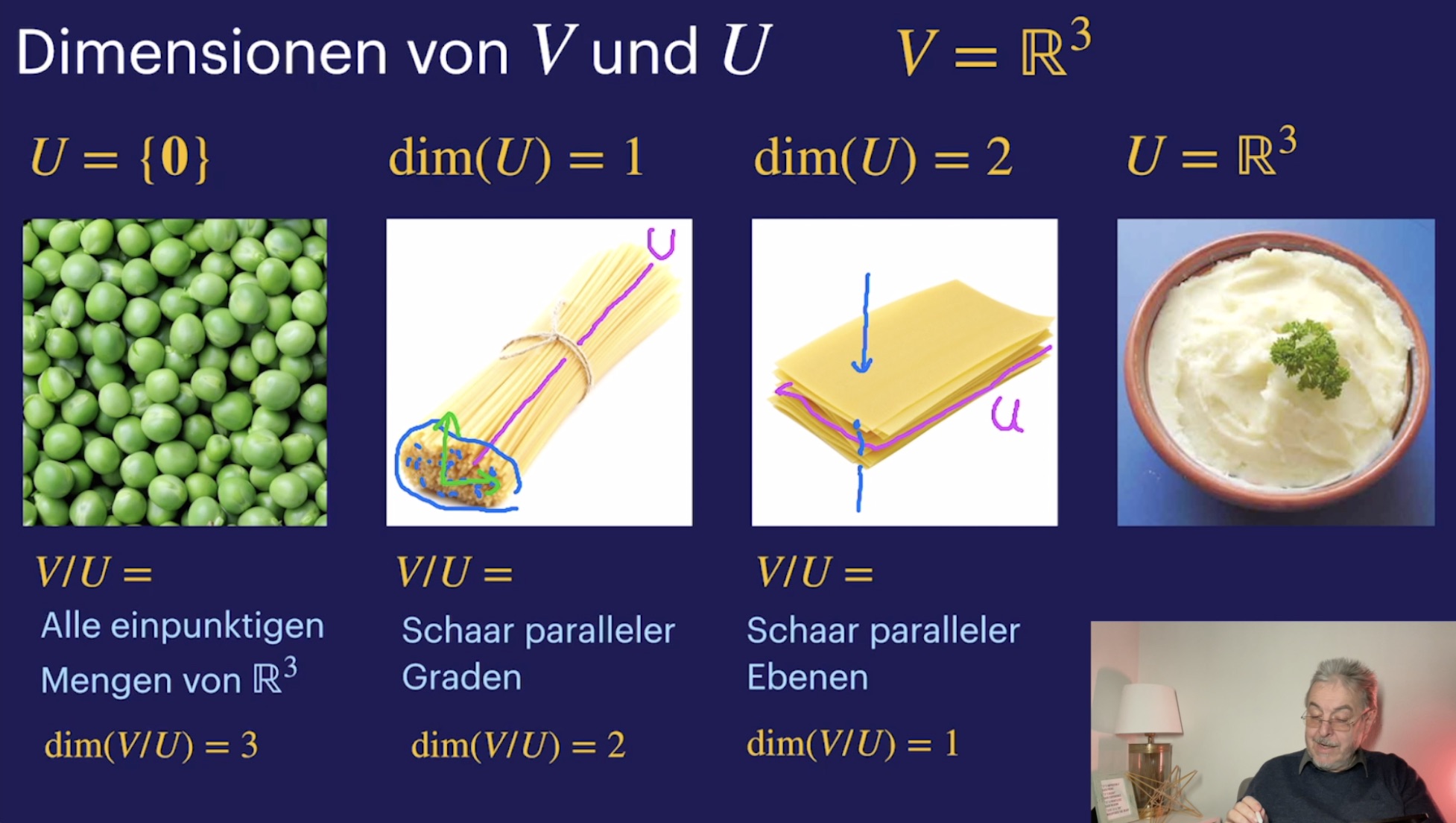
Geometrische Transformationen (31:55)
Koordinaten bezüglich einer Basis (34:41)
Dimensionssatz (43:59)
Isomorphiesatz für Vektorräume (38:58)



Lineare Gleichungssysteme (44:53)
Elementare Zeilenoperationen (45:27)
Inverse einer Matrix (27:23)
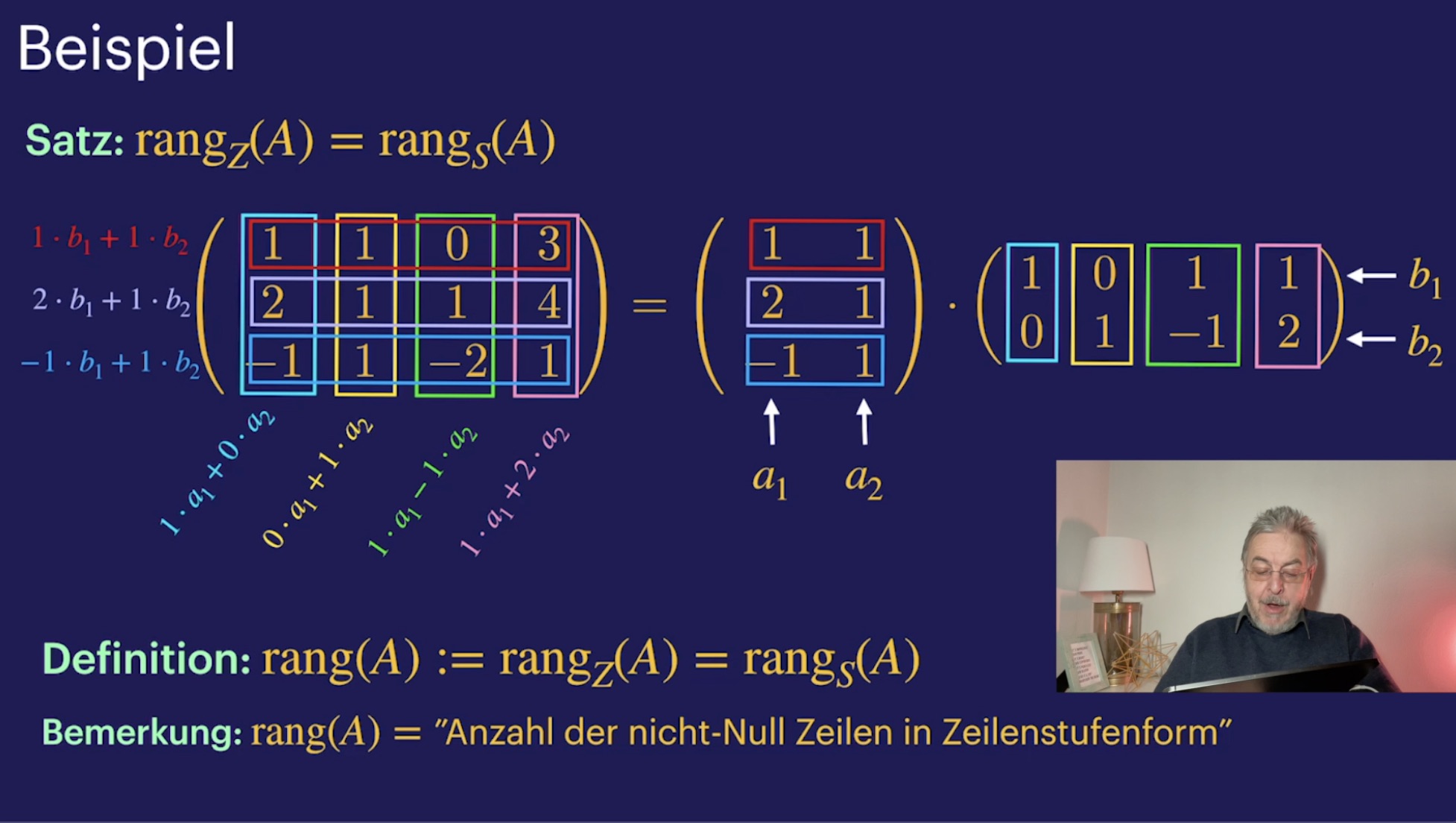
Rang einer Matrix (31:44)
Lineare Algebra 2


Intro und Motivation (9:46)
Determinanten Axiomatik (19:41)
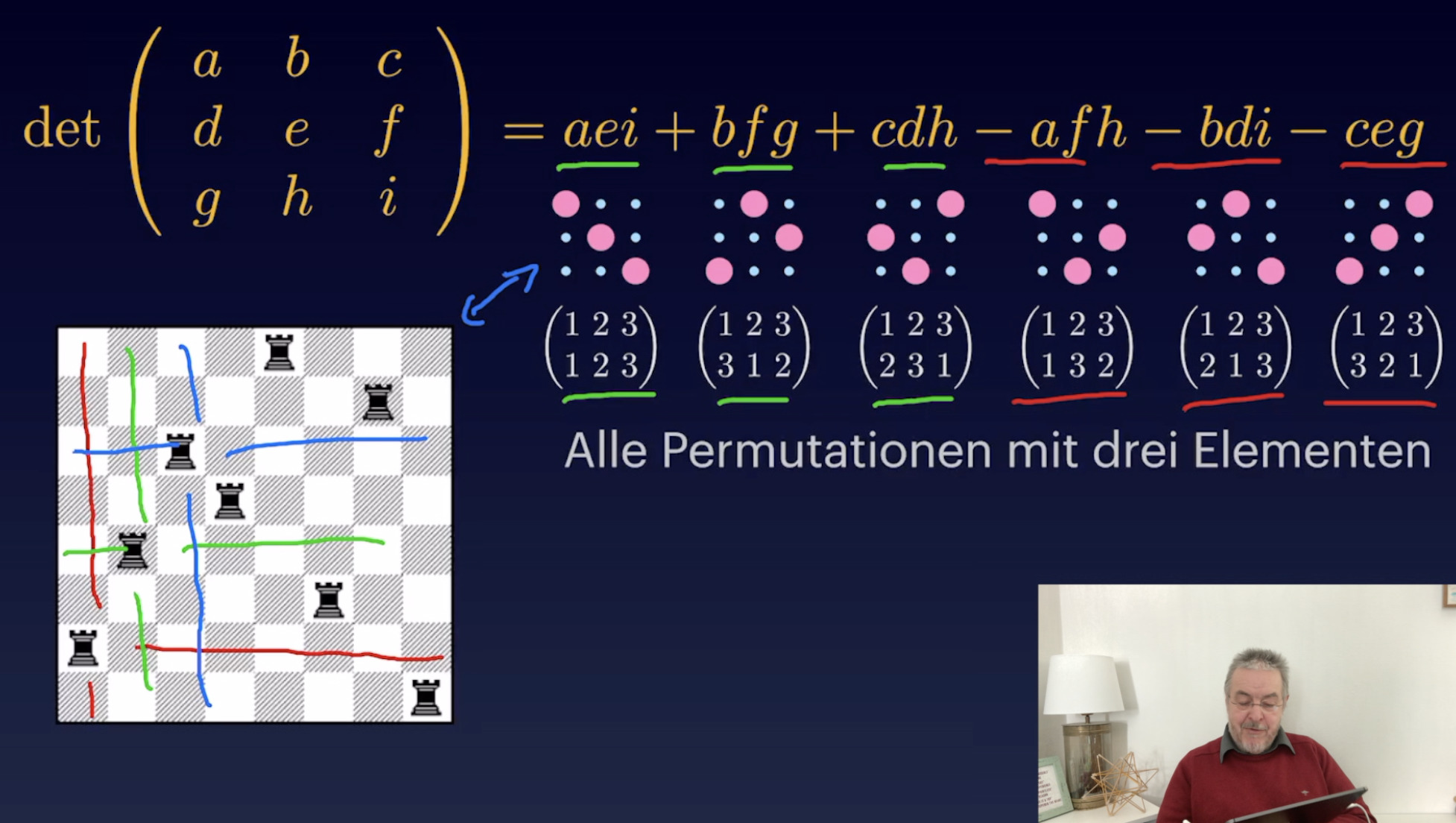
Berechnung Teil 1: Permutationsformel (19:23)
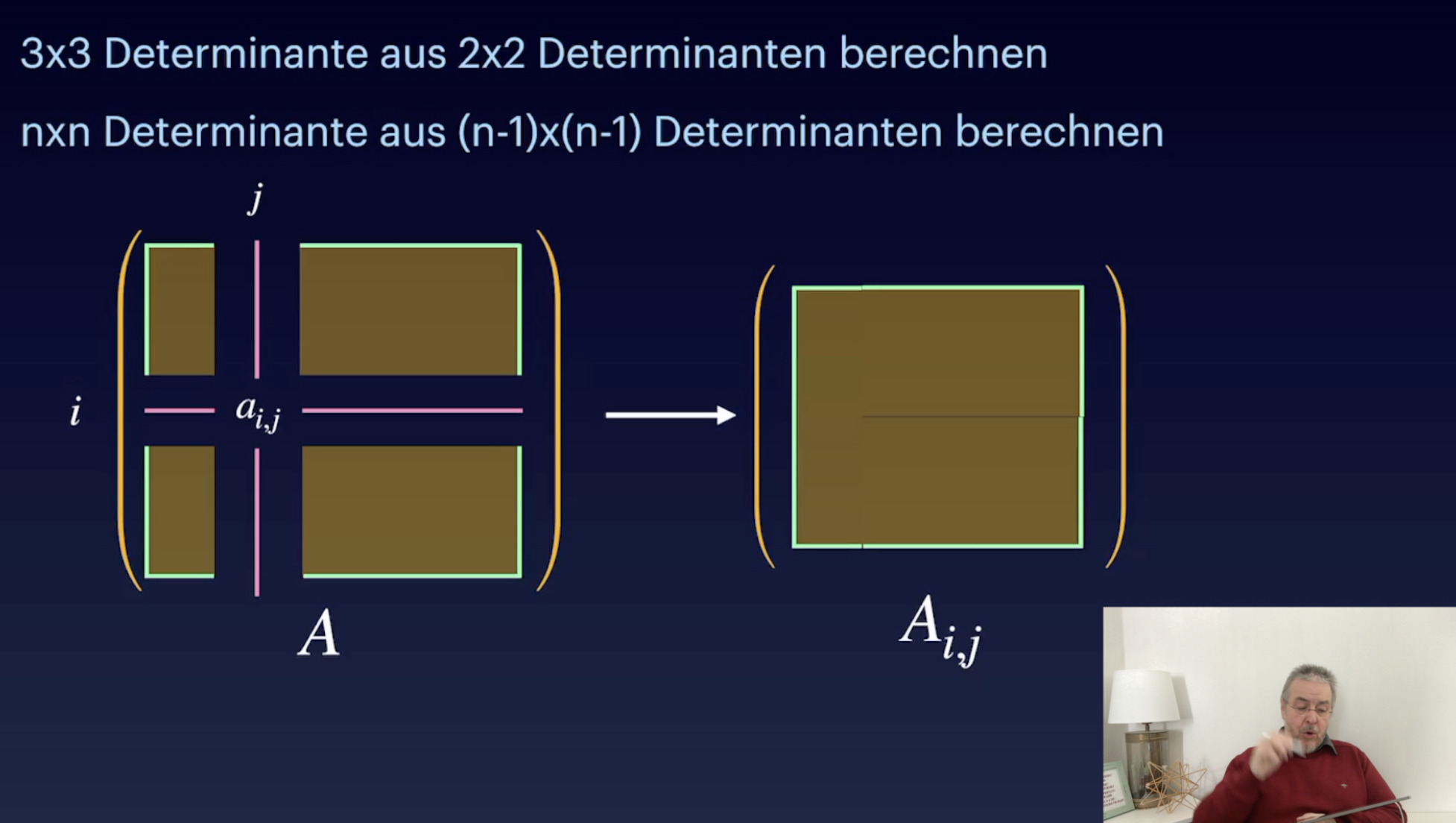
Berechnung Teil 2: Gauss und Spaltenentwicklung (24:07)

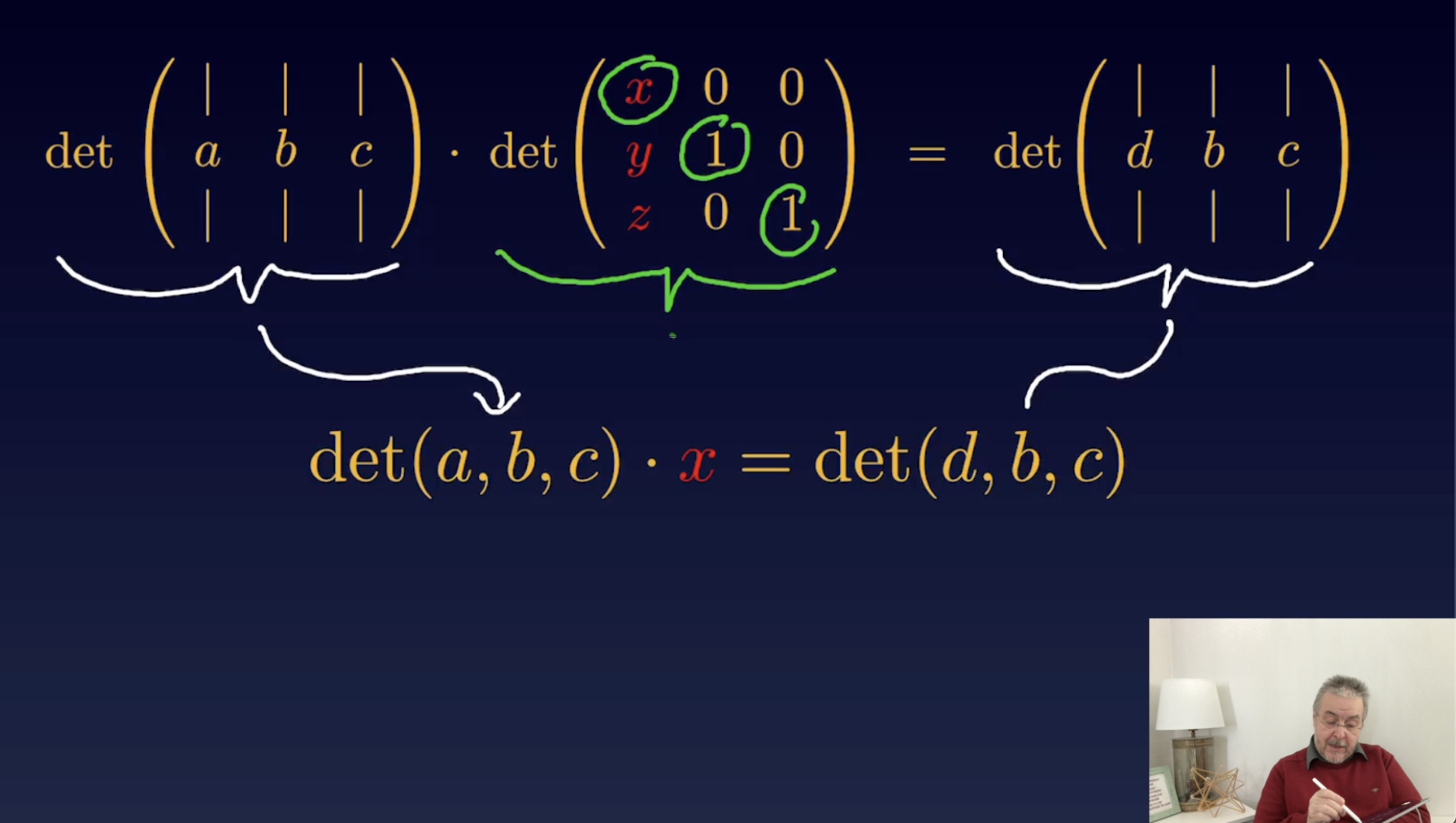
Produktformel (19:31)
Cramer’sche Regel (21:20)
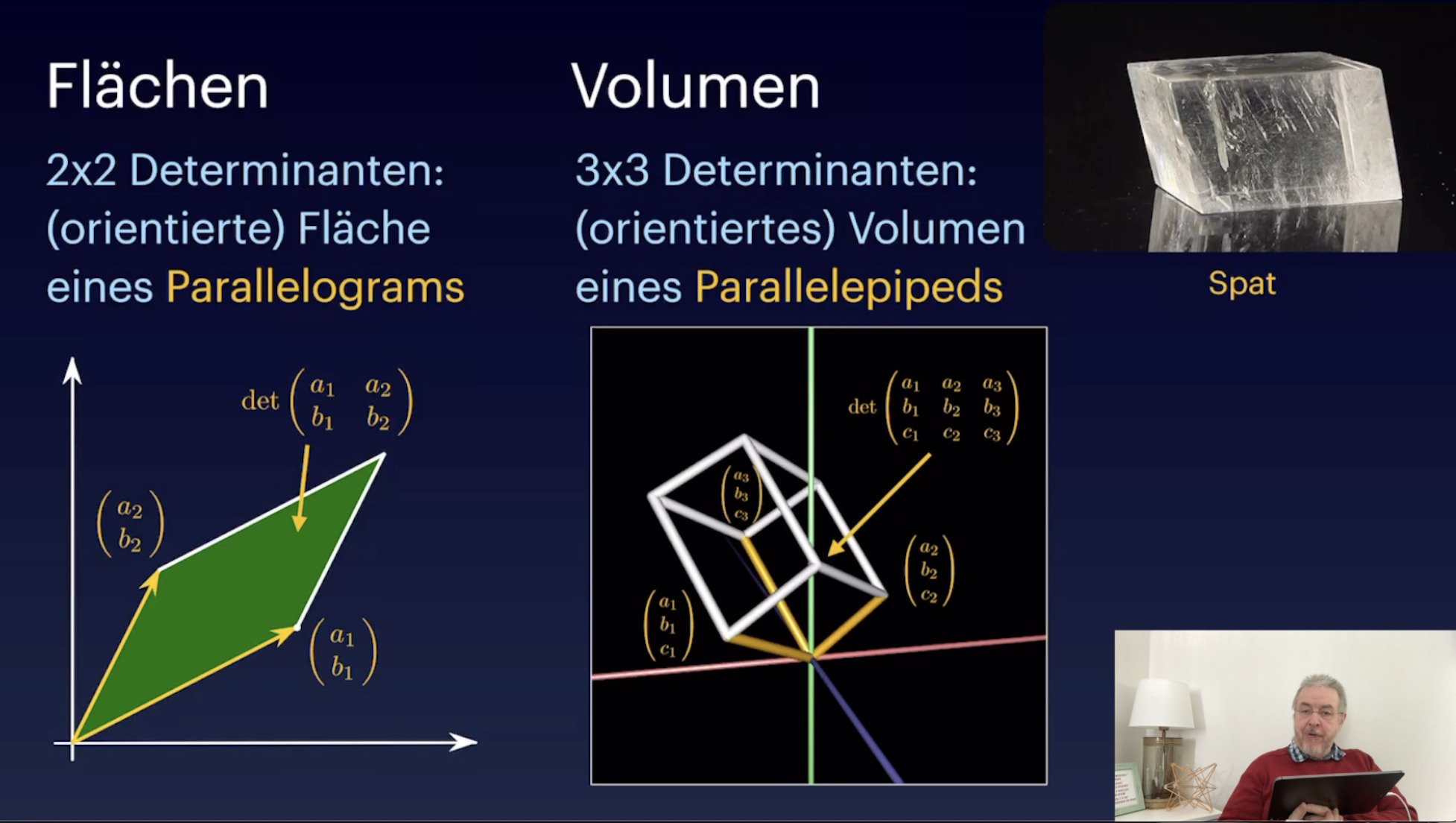
Determinanten und Parallelogramme (19:35)
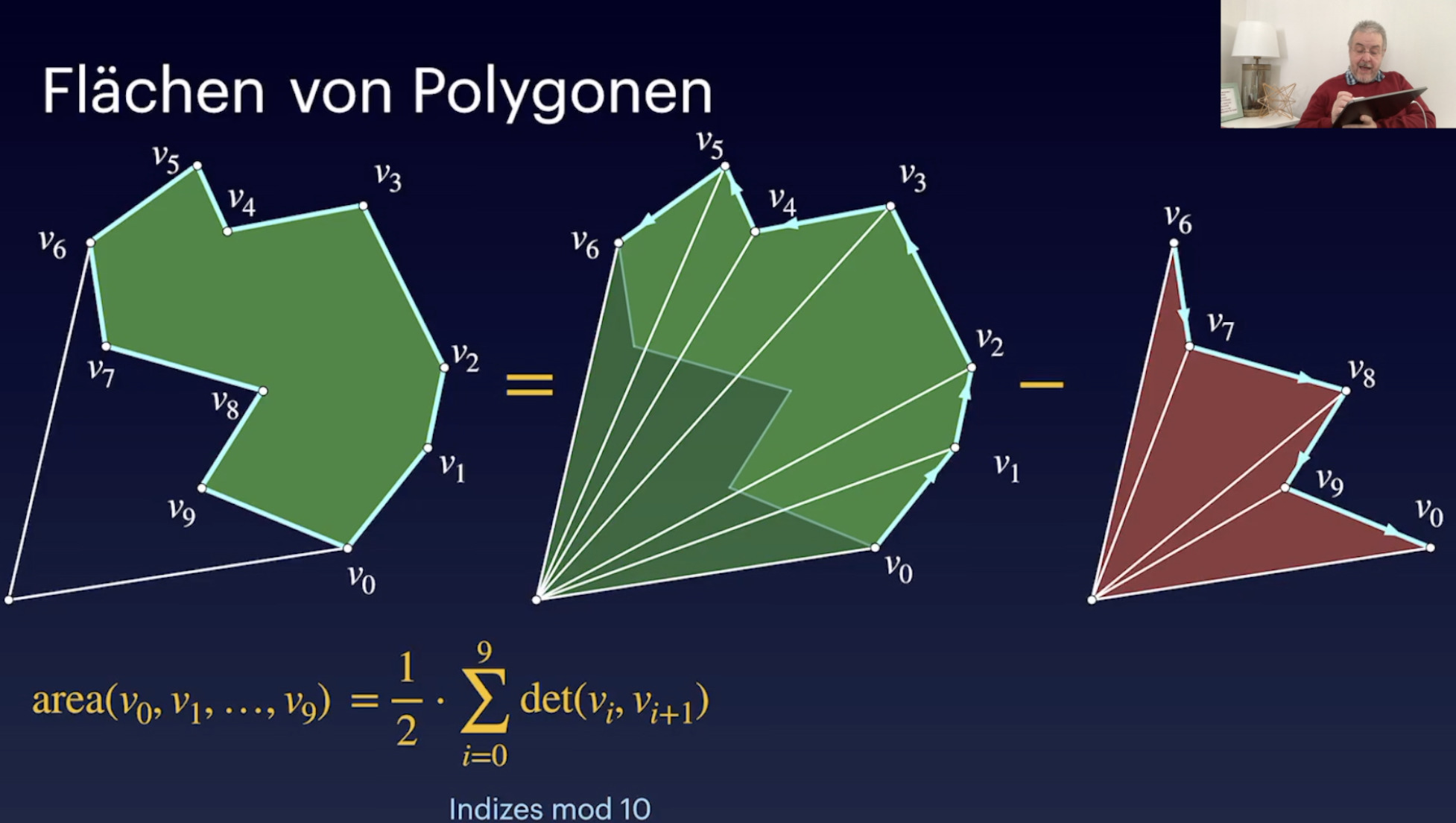
Fläche Beliebiger Polygone (27:26)
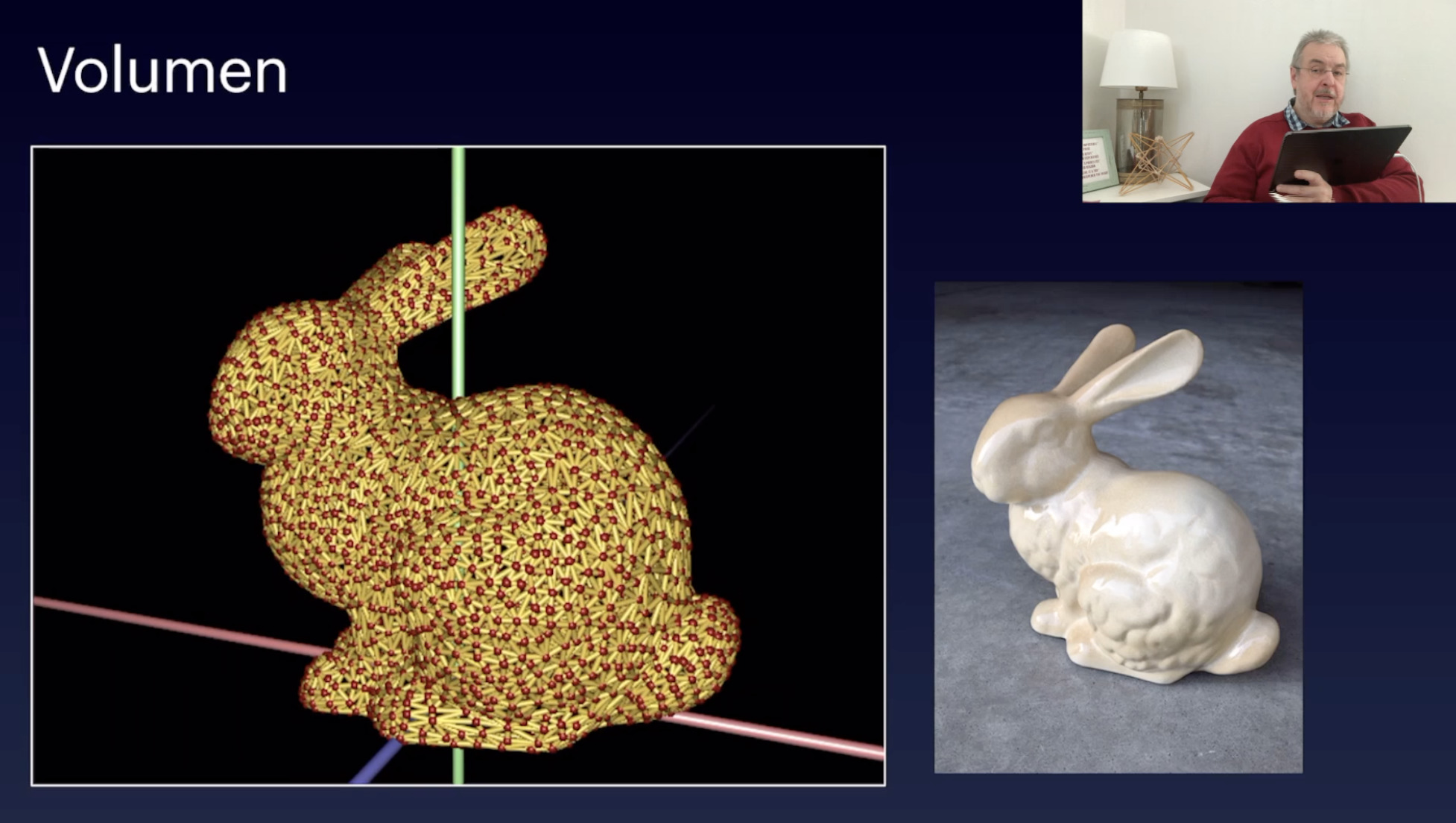
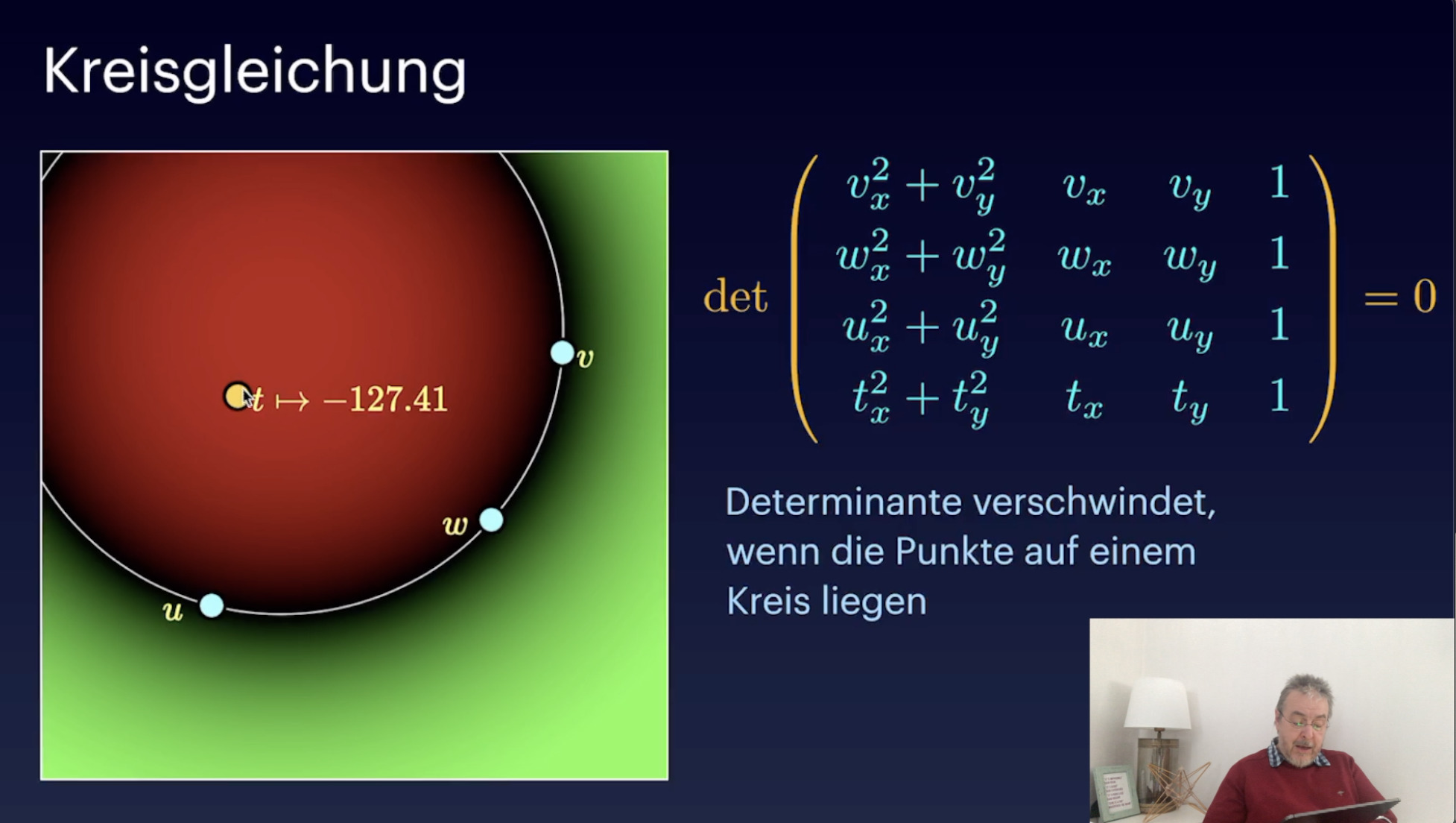
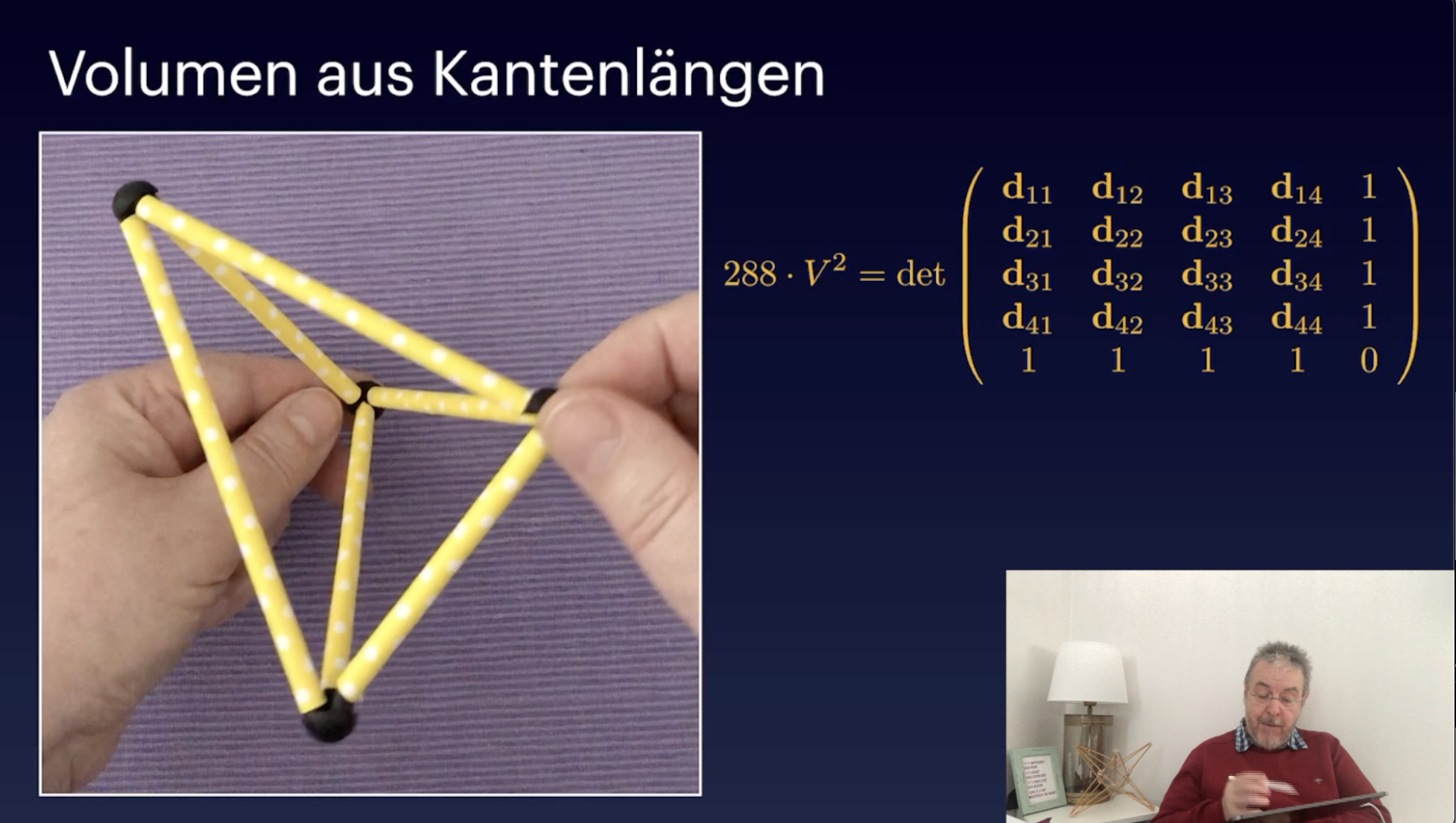
Volumen (15:32)
Determinanten und Vorzeichen (20:22)
Inkreis Prädikat (20:34)
Cayley Menger Determinante (20:19)




Volumenverzerrung einer Abbildung (17:04)
Operationen: Vektoren/Vektoren & Vektoren/Matrizen (24:31)
Operationen: Matrizen/Matrizen (26:50)
Eigenvektor Motivation (9:49)

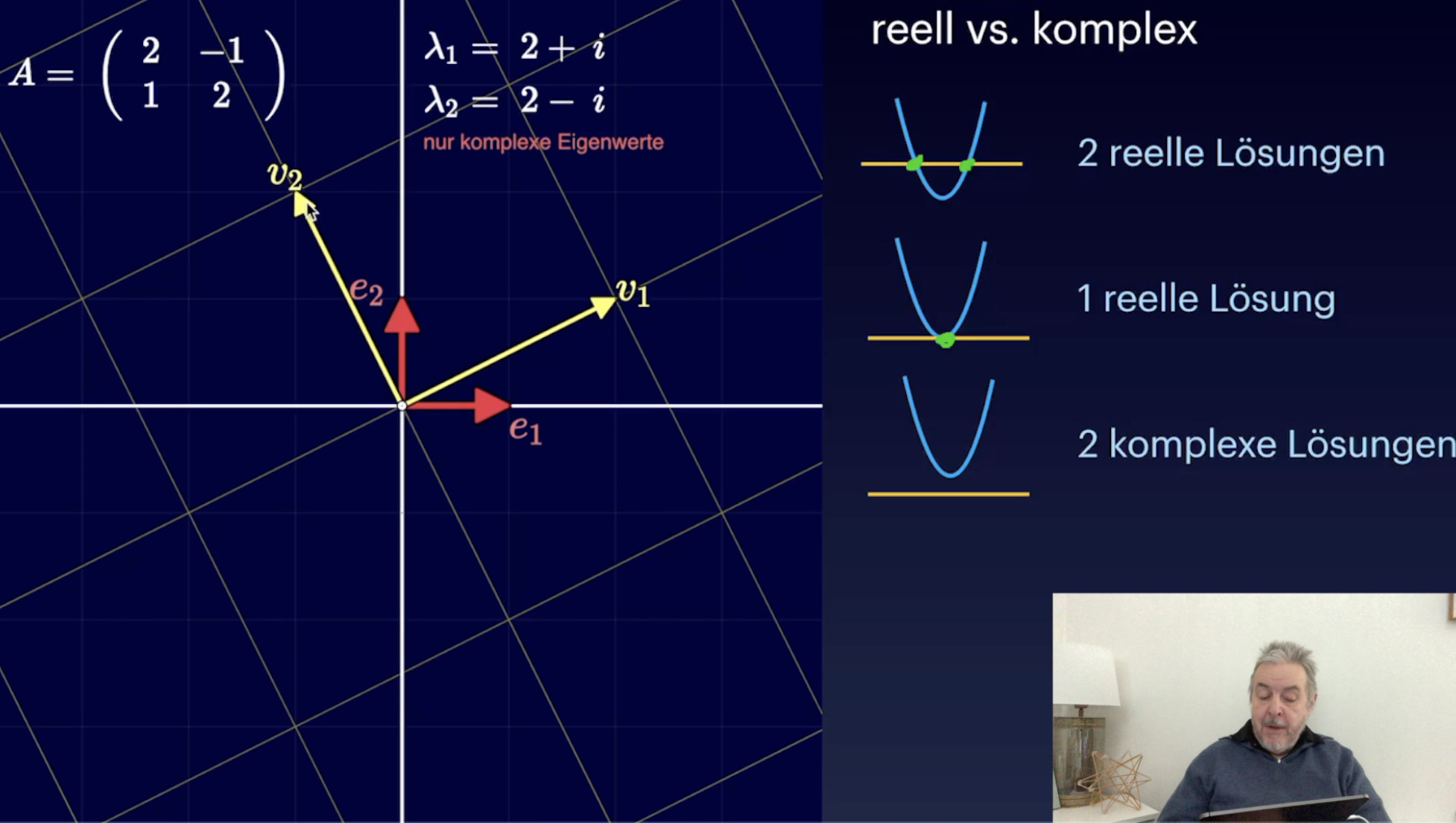
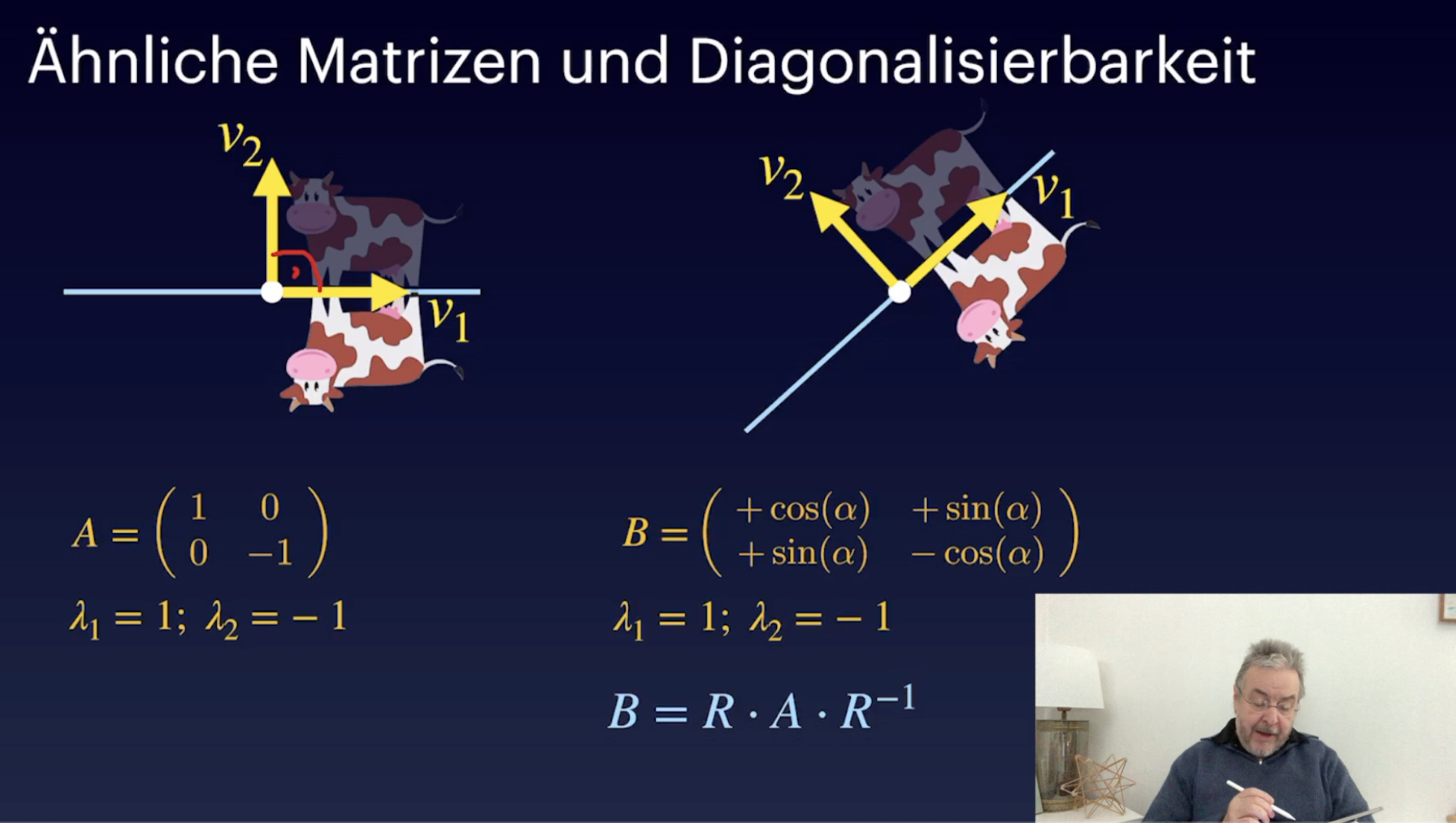

Geometrie Linearer Abbildungen (26:24)
Eigenvektor, Eigenwerte Definition und Berechnung (31:39)
Ähnliche Matrizen, Diagonalisierbarkeit (25:26)
Wichtige Formeln für Eigenwerte (28:06)
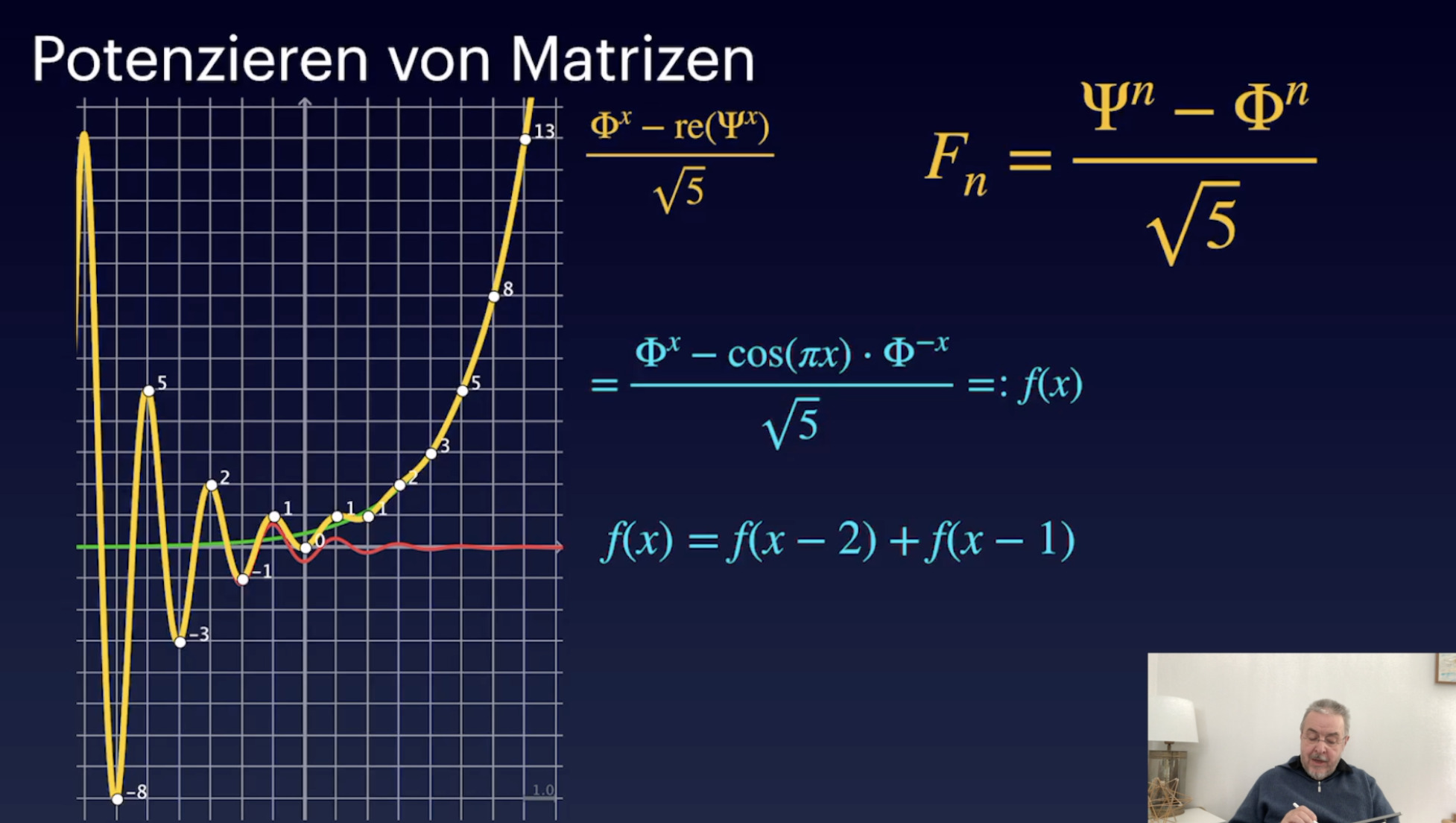
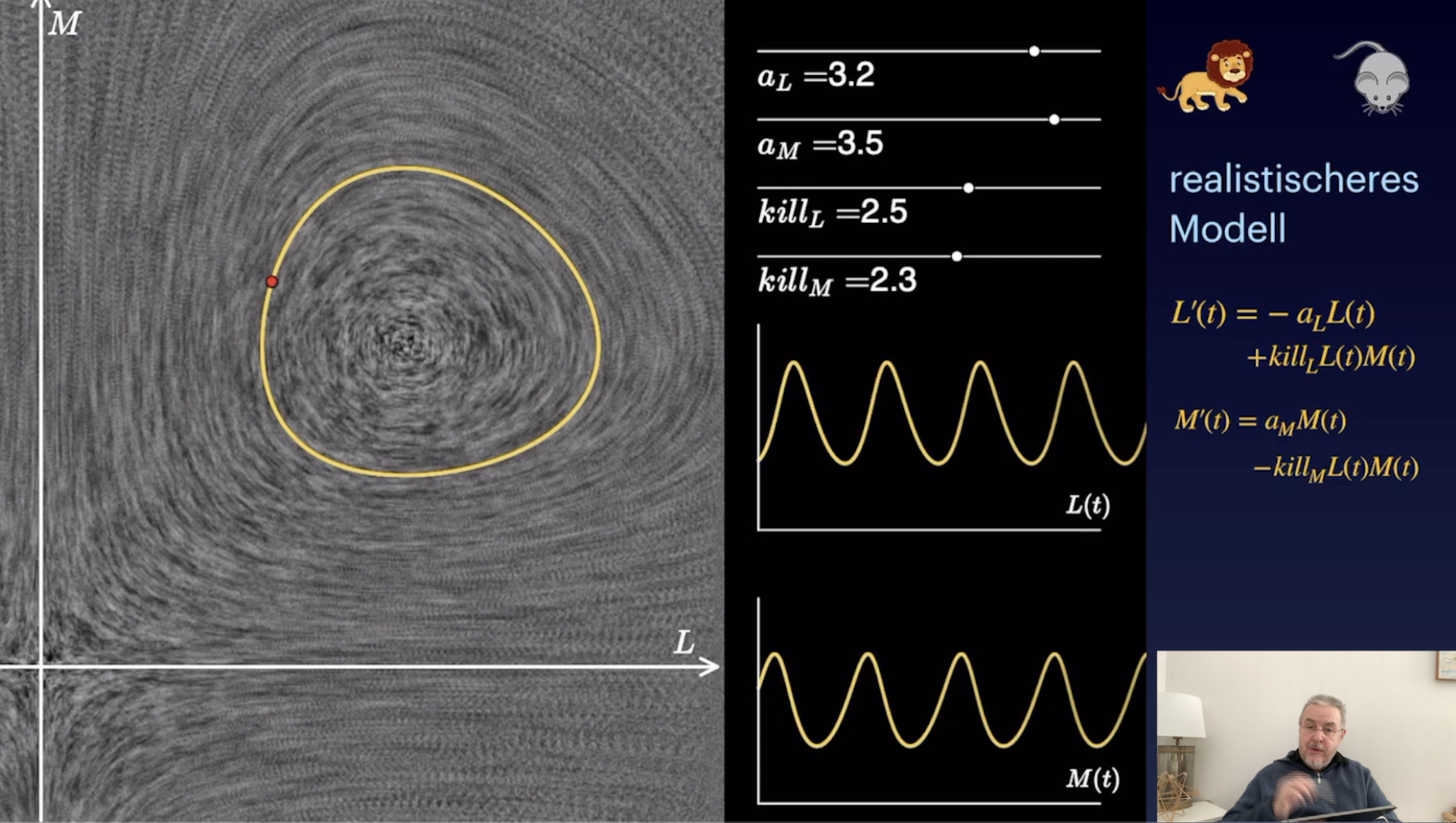


Potenzen von Matrizen (27:06)
Lineare Systeme von Differentialgleichungen (26:32)
Lineare Systeme von Differentialgleichungen II (13:03)
Harmonische Schwingungen (30:44)




Längen, Winkel und Produkte, Einführung (8:13)
Kanonisches Skalarprodukt (29:53)
Allgemeines Skalarprodukt (27:18)
Längen und Normen (27:19)

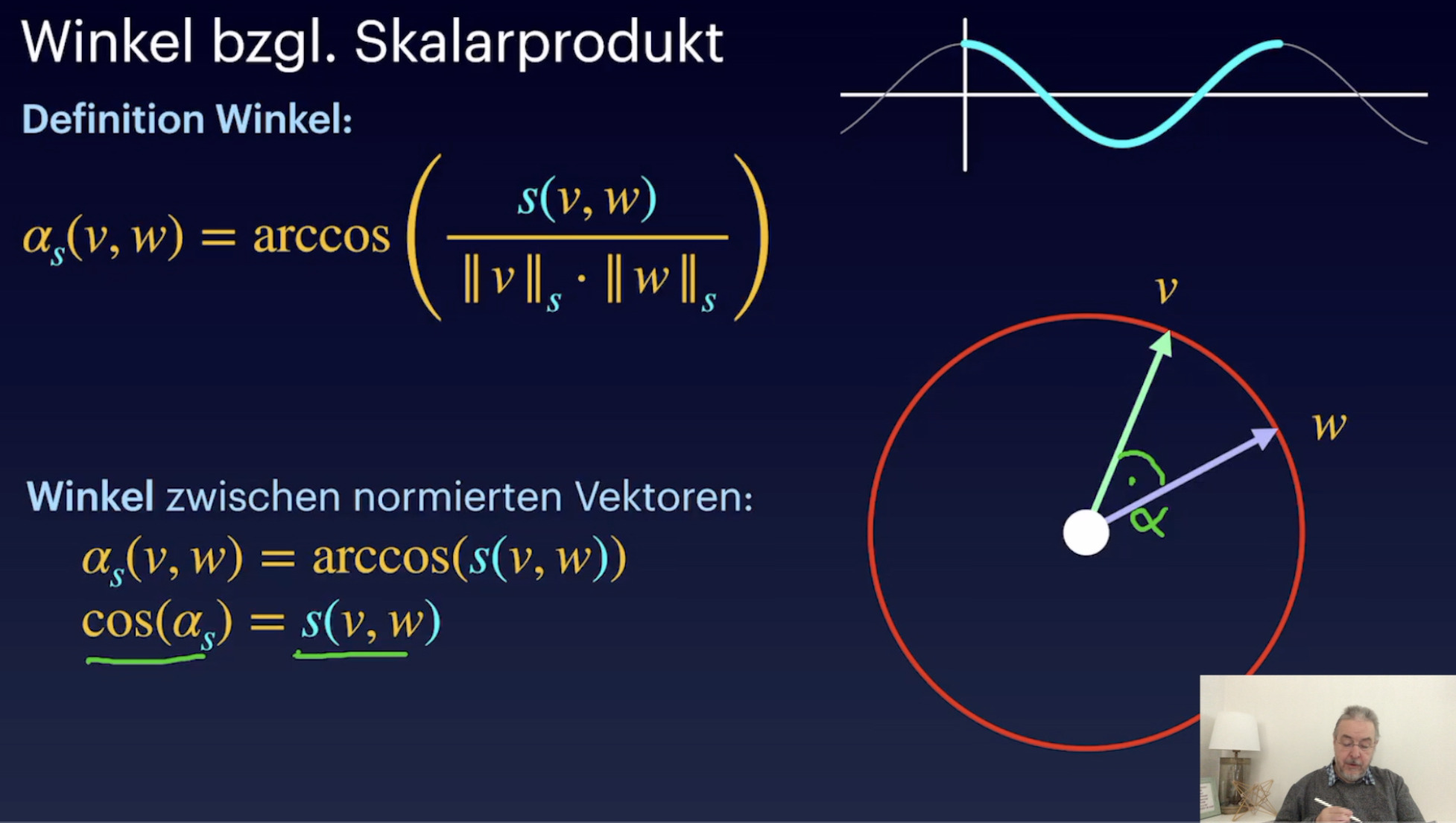
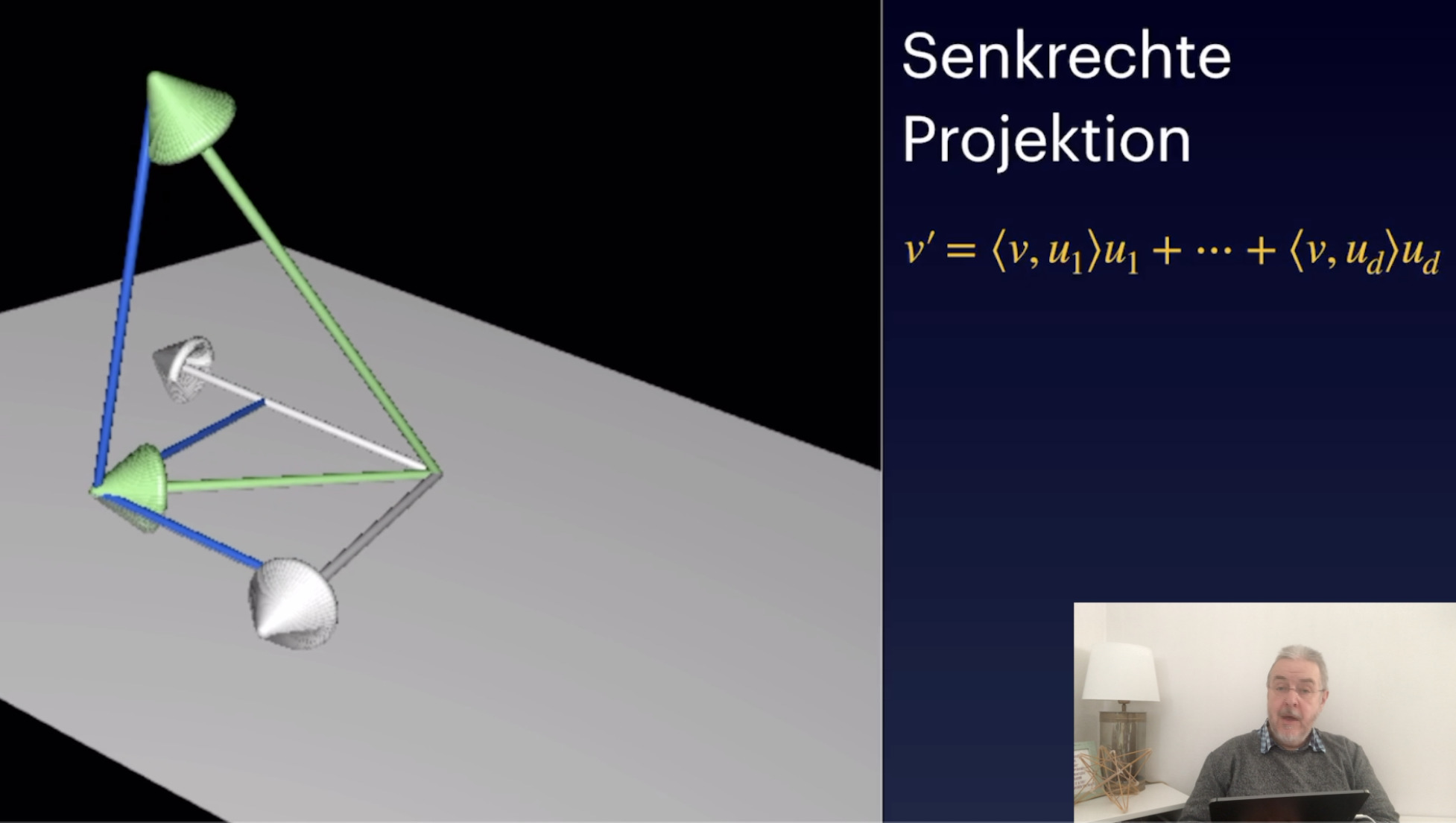

Winkel und CSU (31:15)
Orthogonalbasen I (14:28)
Orthogonalbasen II (22:15)
Gram Schmidt und senkrechte Projektion (20:13)


Ausgleichsrechnung (36:55)
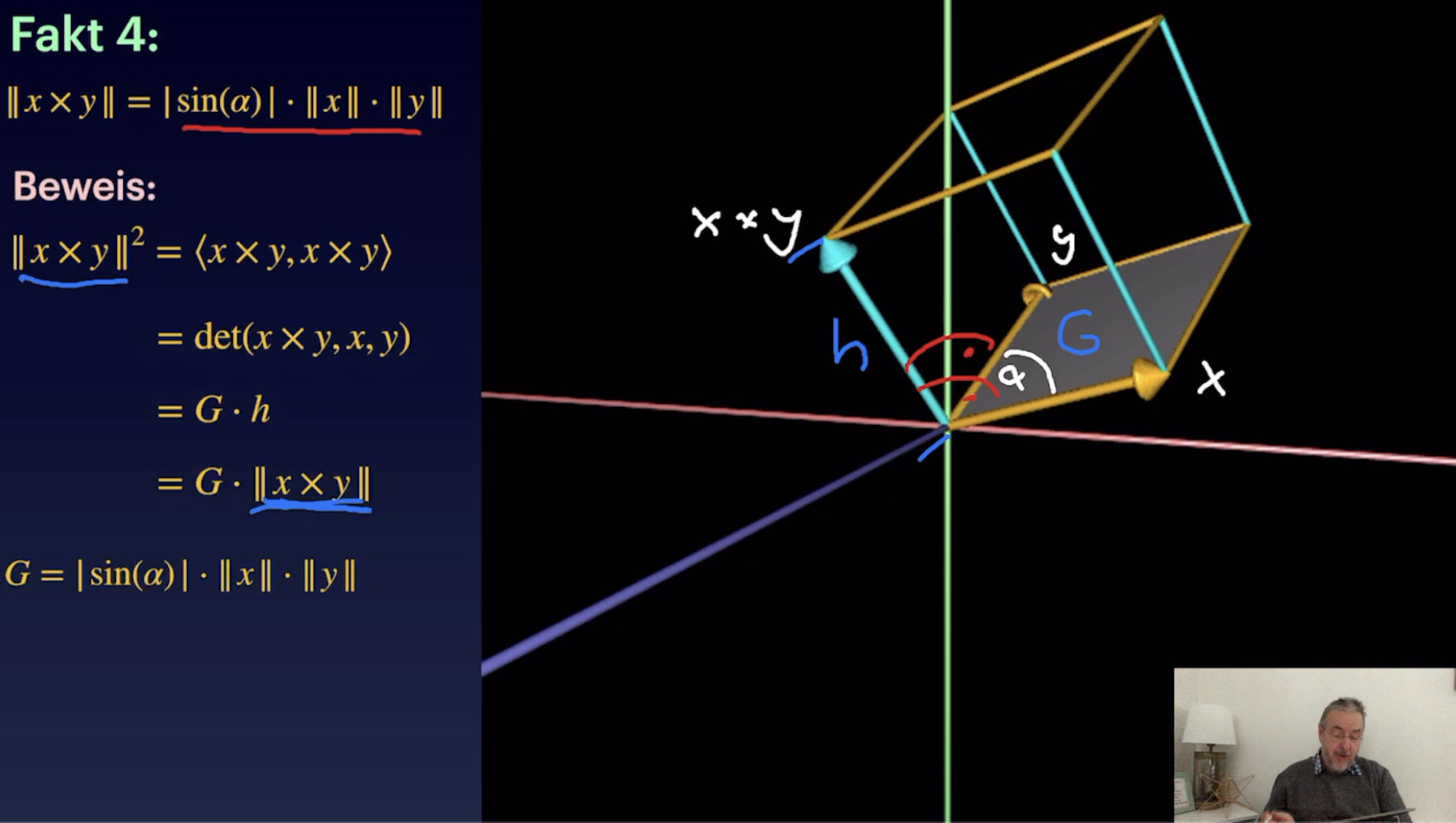
Kreuzprodukt (17:36)
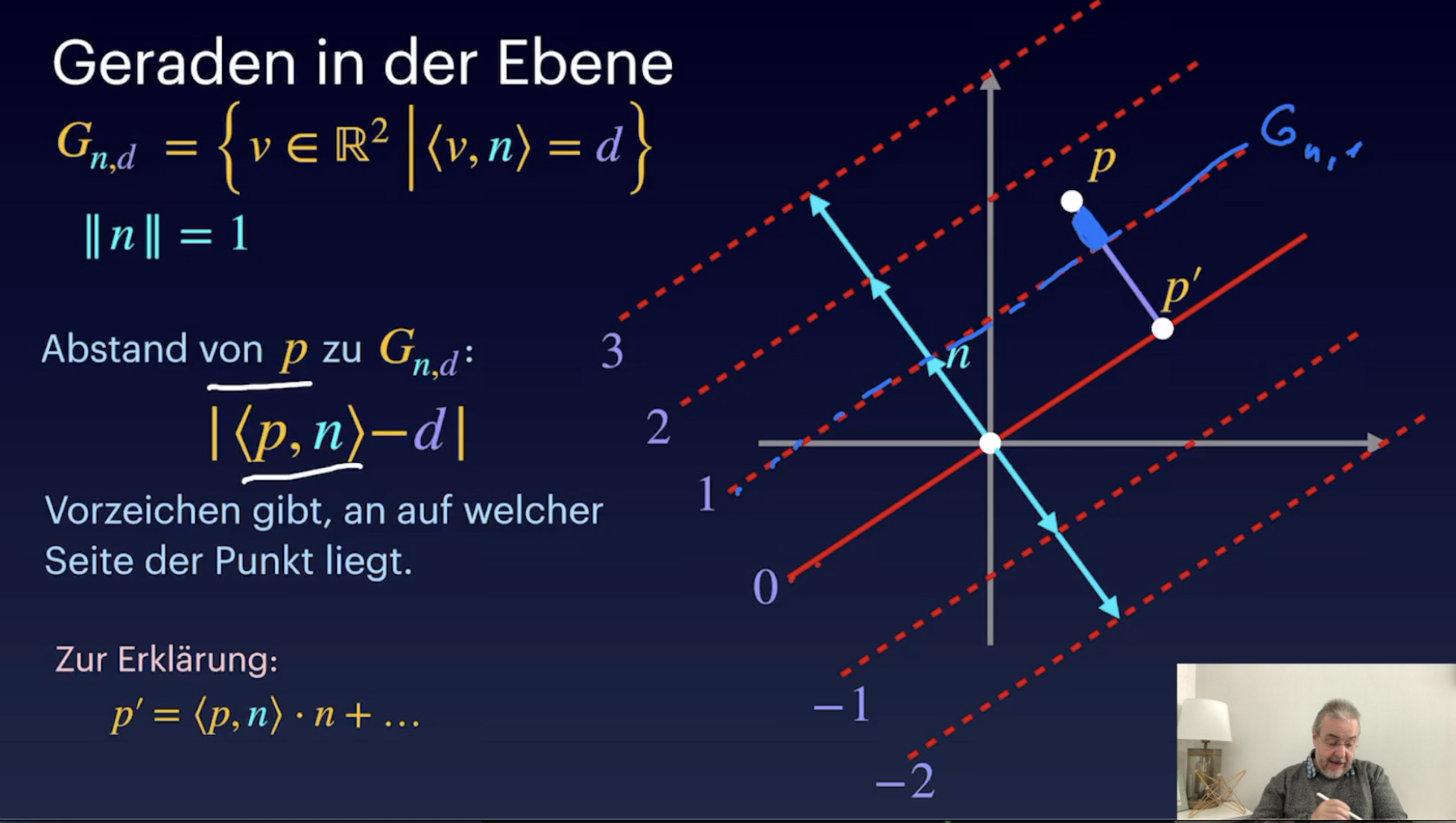
Hesse’sche Normalform (23:39)
Sesquilinearform (17:35)

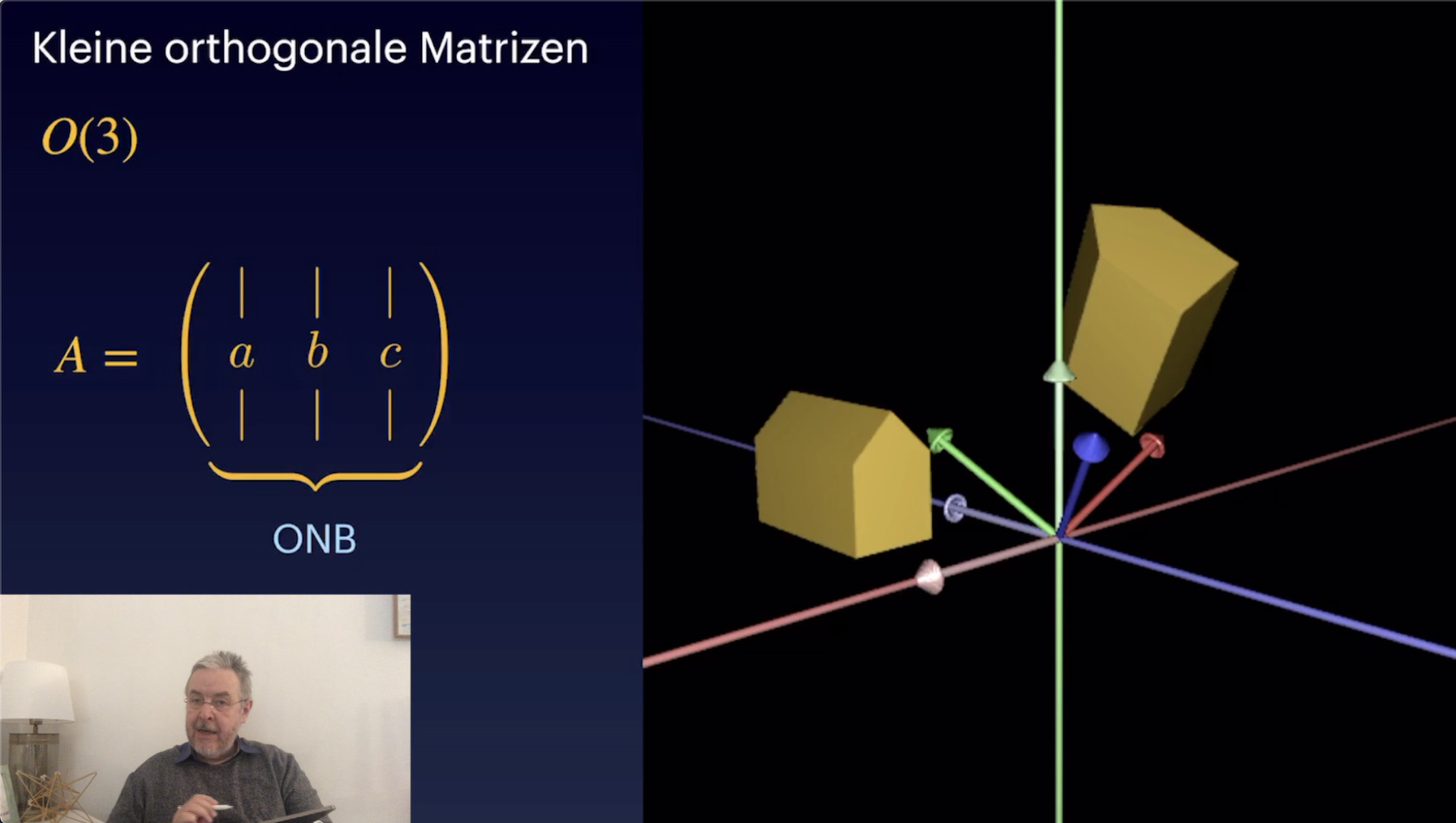
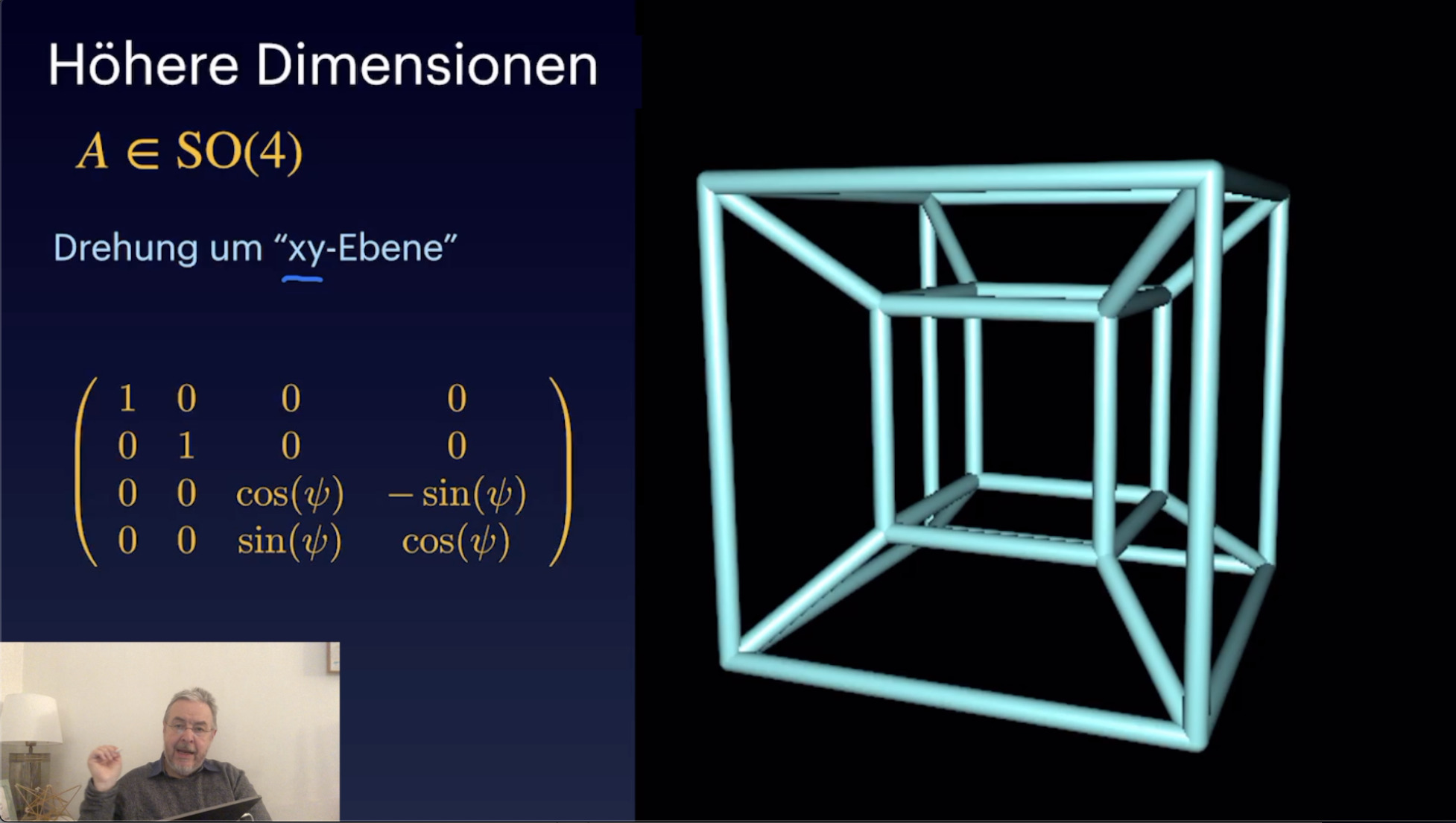
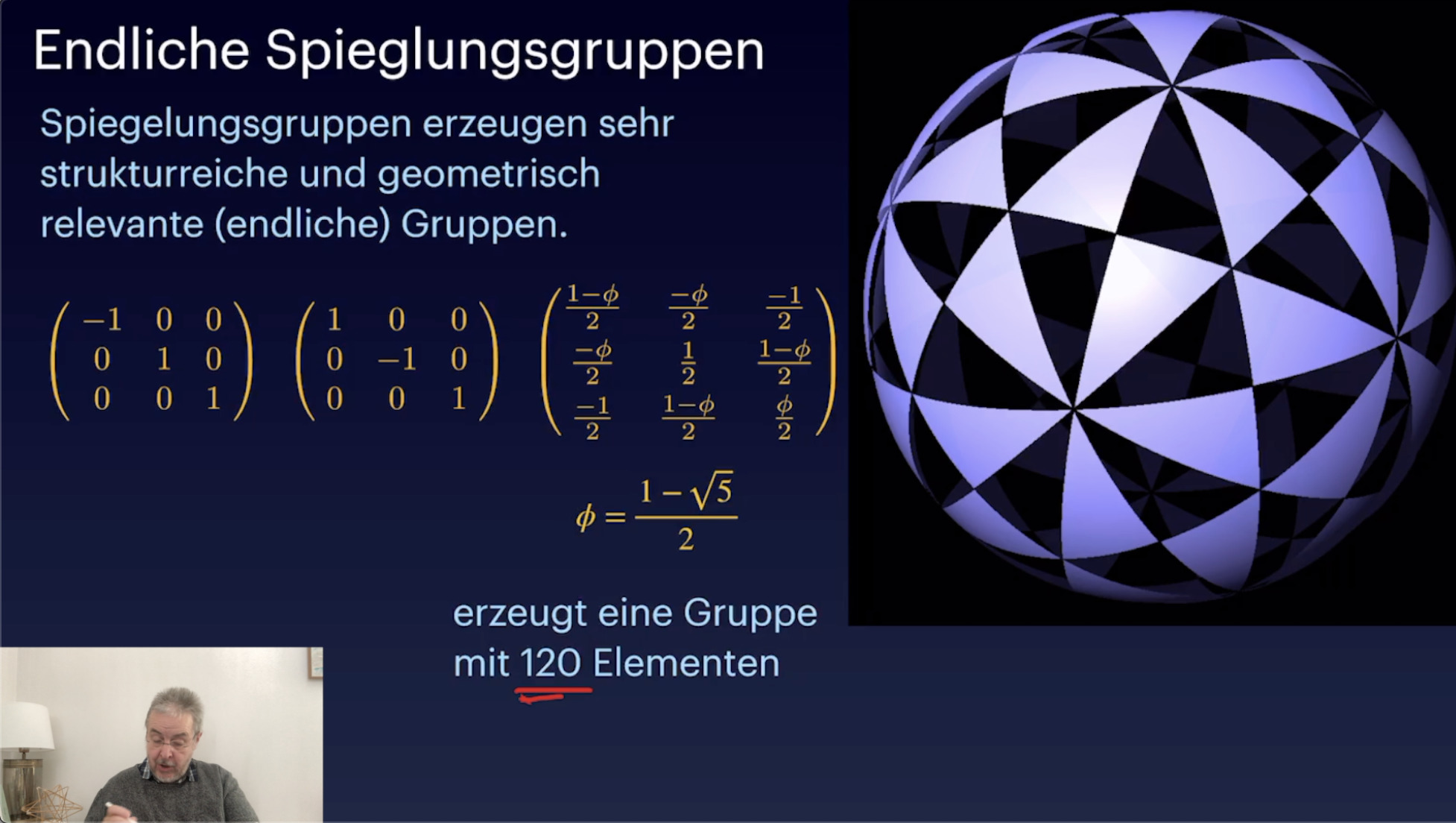
Matritzengruppen (29:47)
Orthogonale Matrizen (35:56)
Drehmatrizen (26:06)
Spiegelungsmatrizen (39:43)

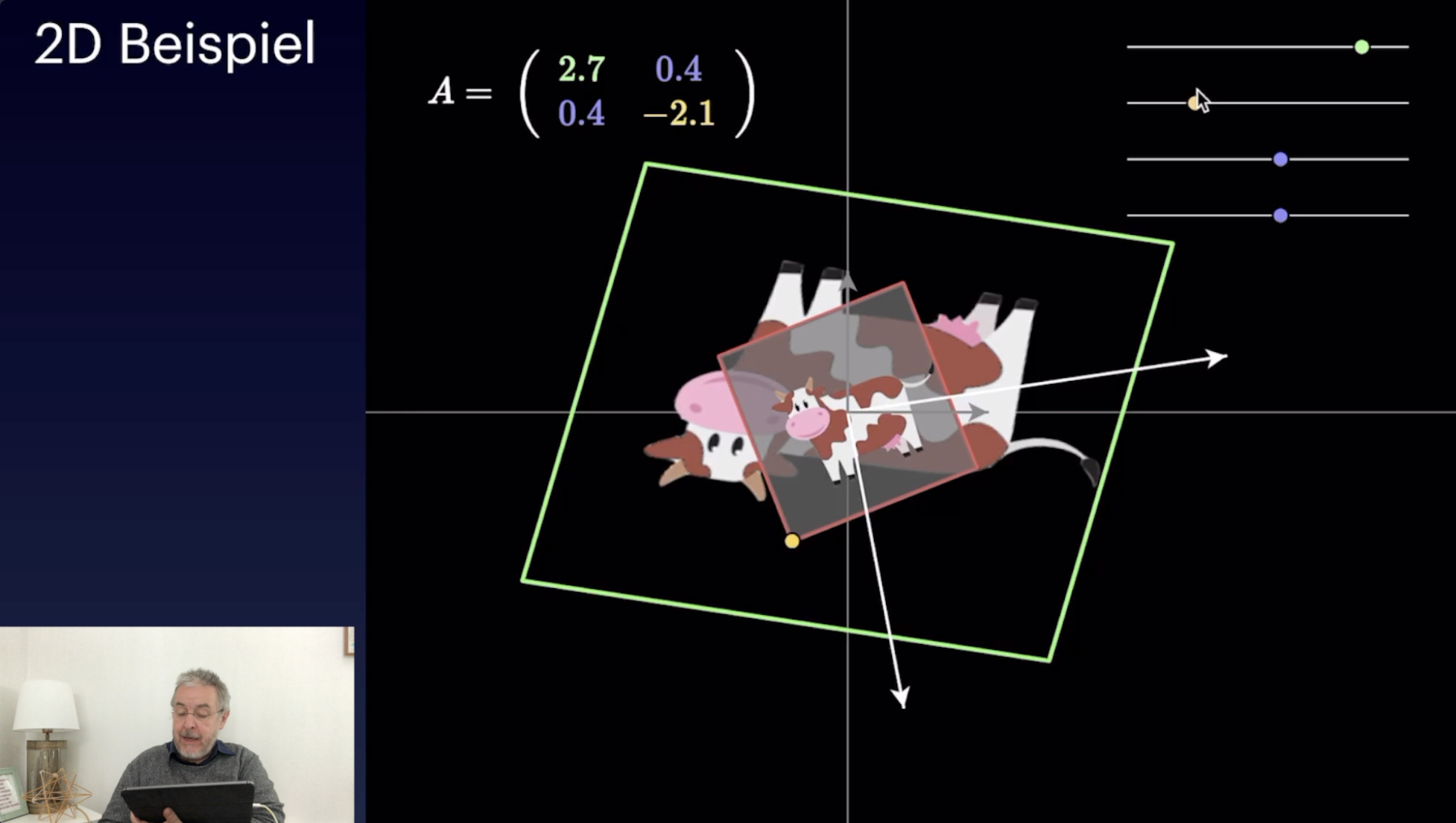

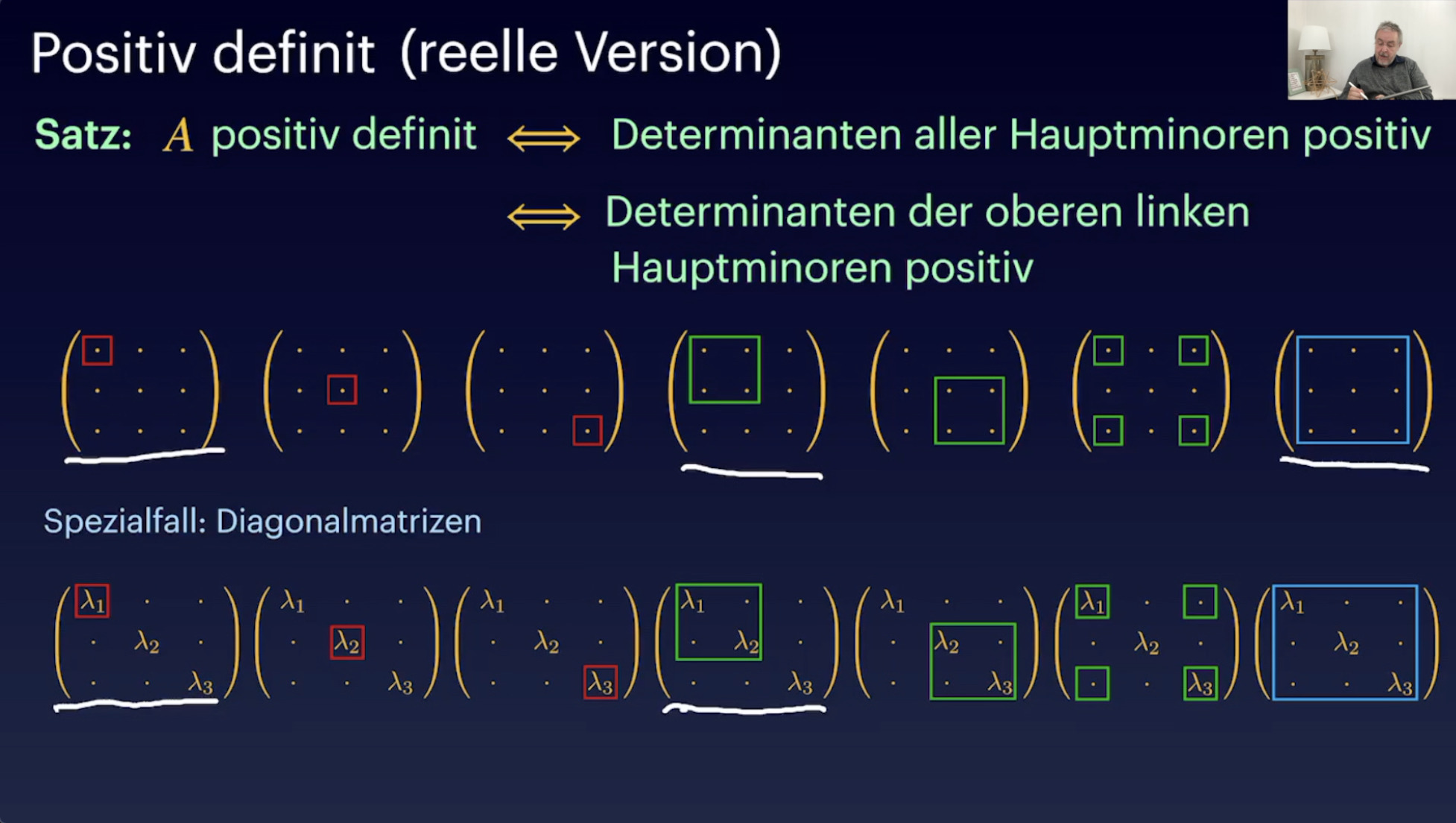
SU(2) (58:53)
Eigenwerte Symmetrischer Matrizen (17:51)
Eigenwerte Symmetrischer Matrizen (Beweise) (28:52)
Skalerprodukte ein zweiter Blick (28:47)
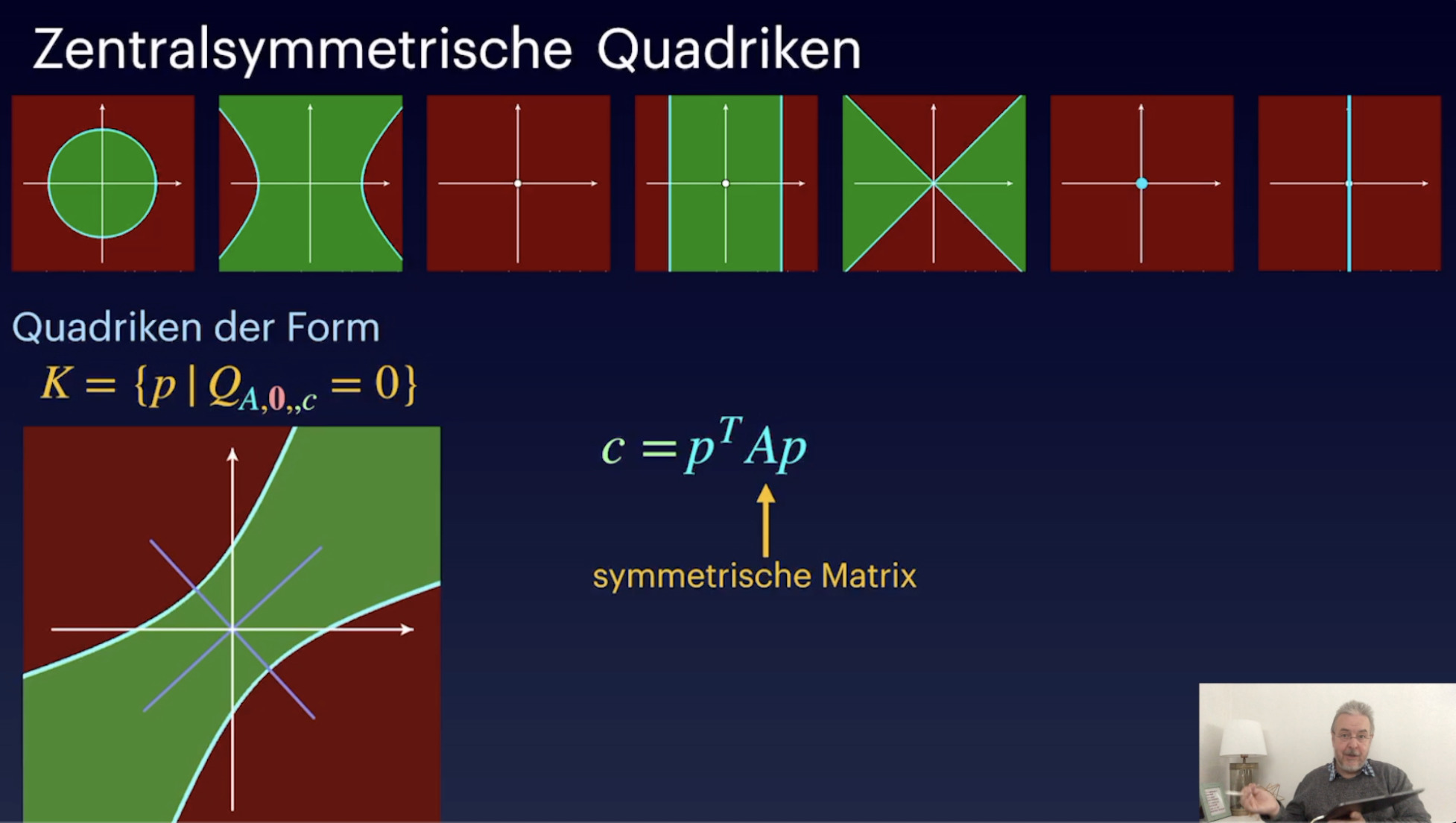
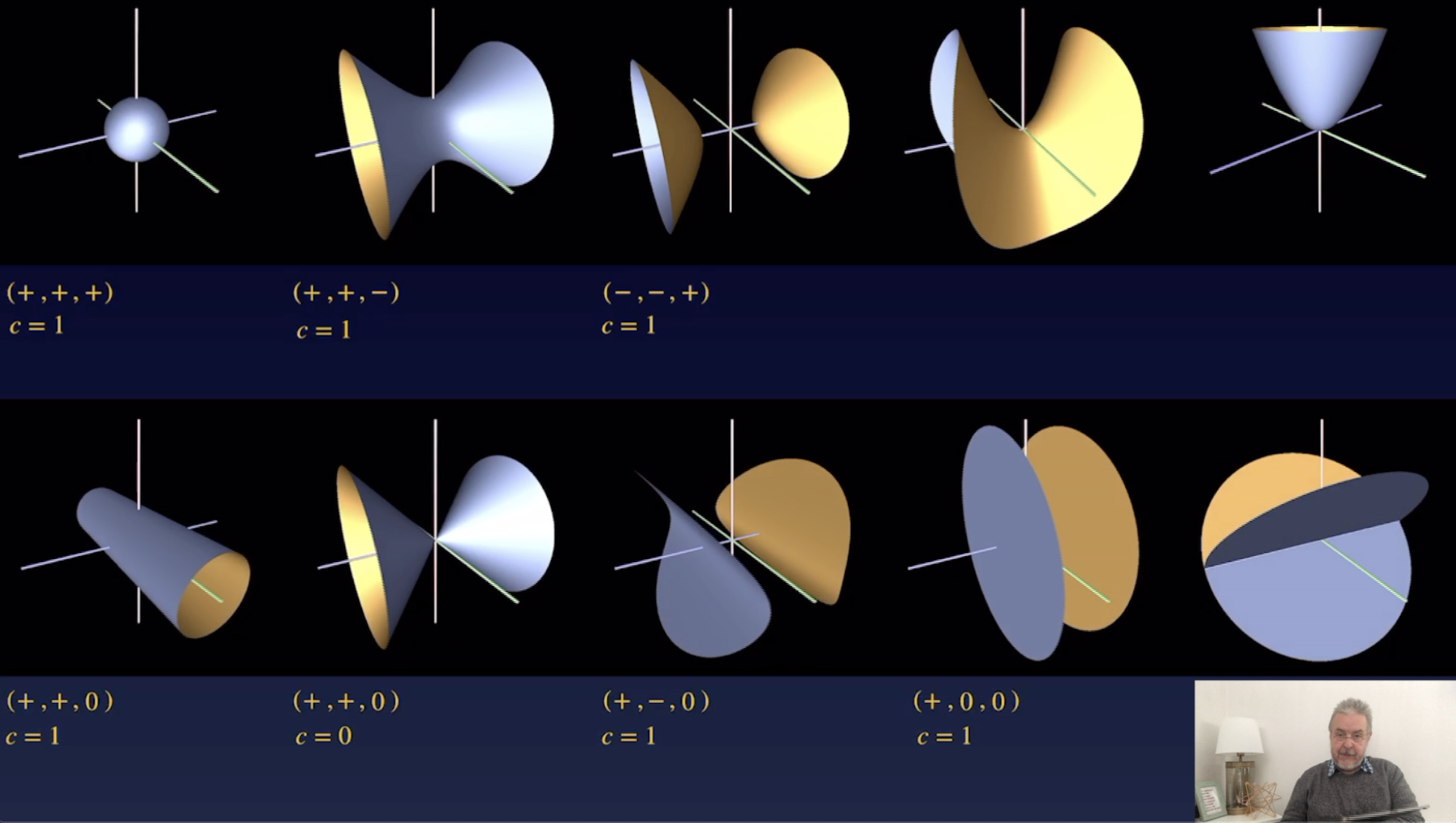

Quadriken (29:12)
Klassifikation von Quadriken (18:43)
Geometrie von Quadriken (19:26)
Geometriekalküle
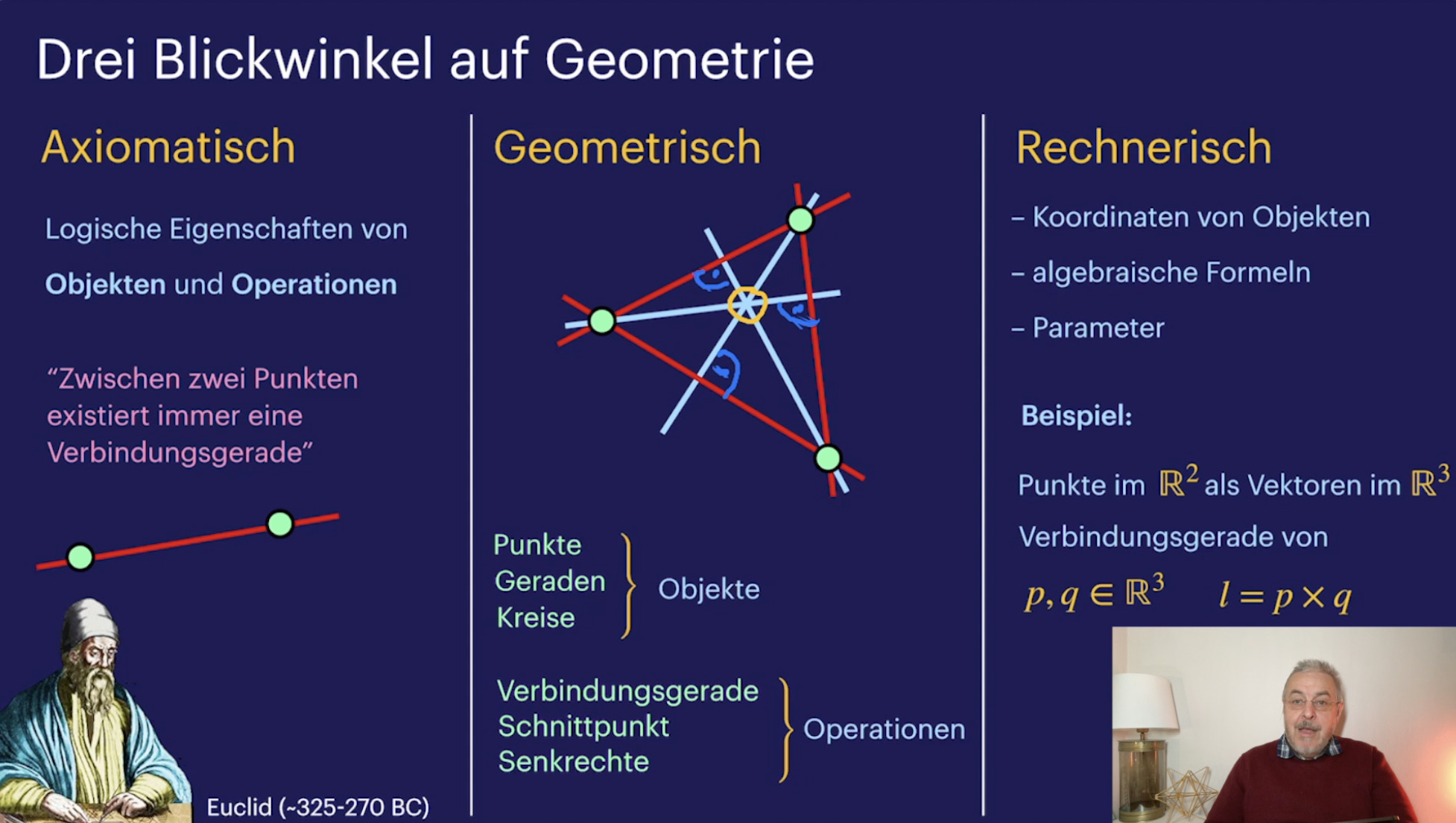
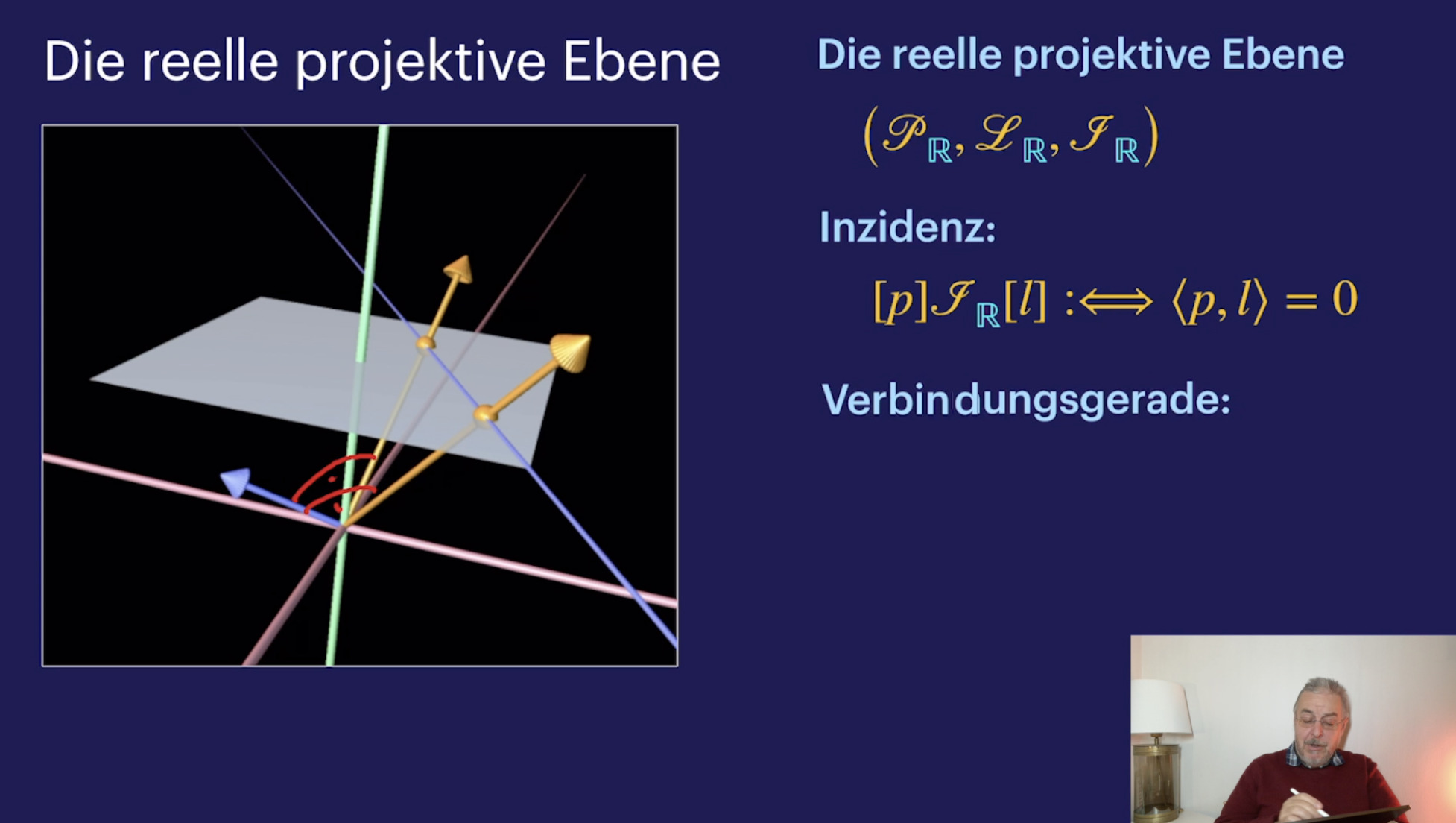
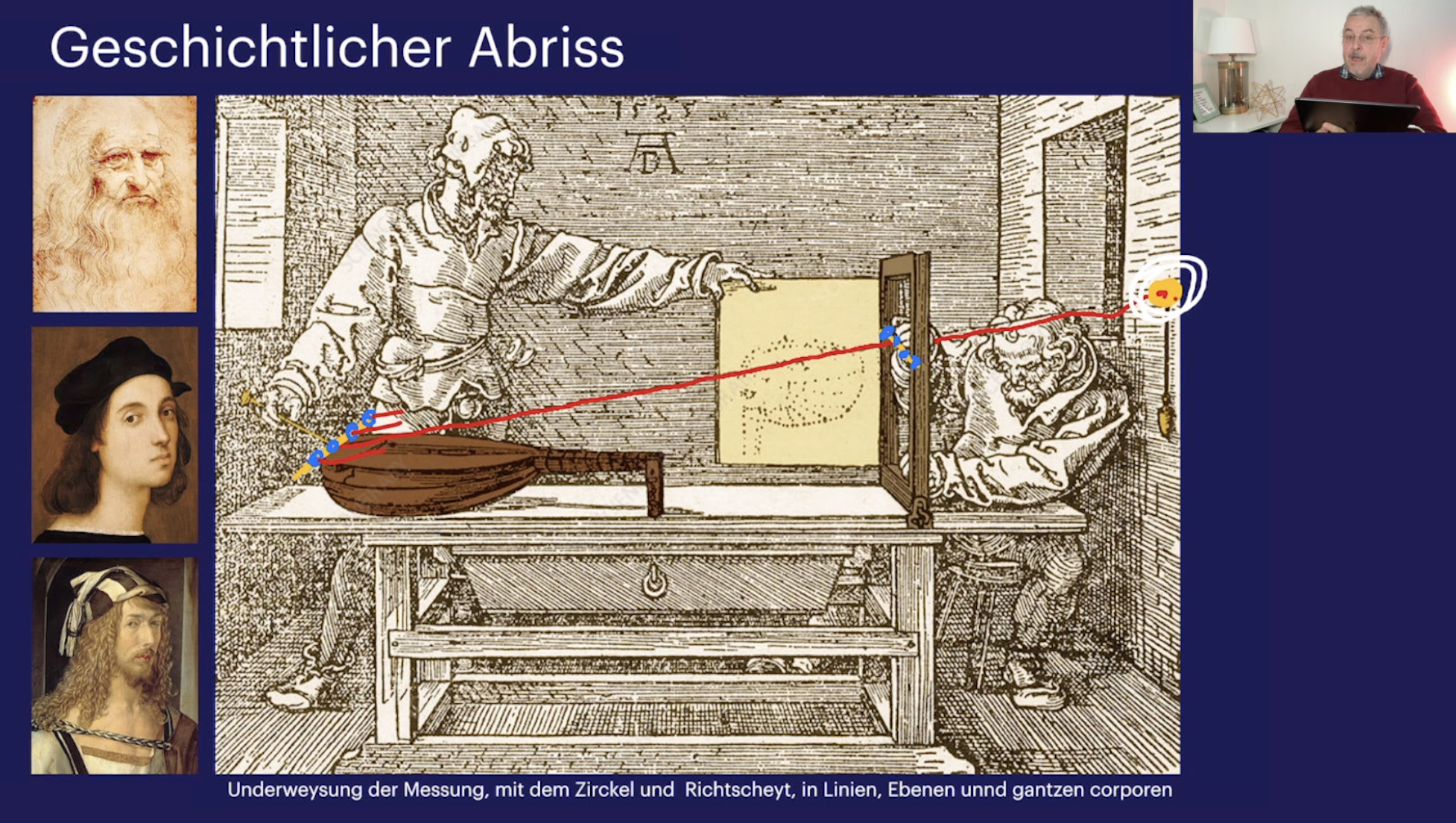
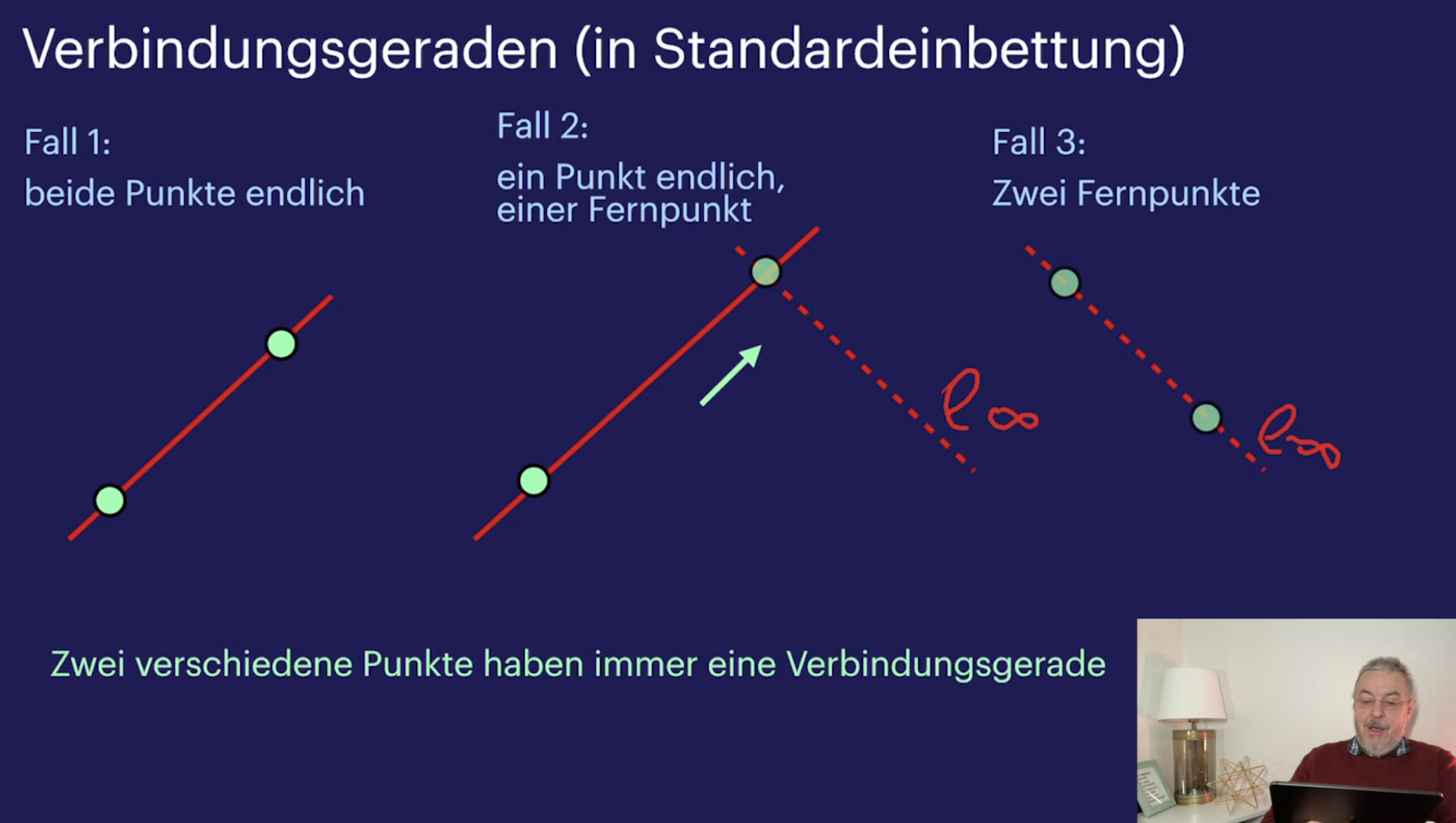
Einführung (22:36)
Homogene Koordinaten (28:33)
Geschichtlicher Abriss (22:36)
Inzidenz, Join, Meet (34:22)


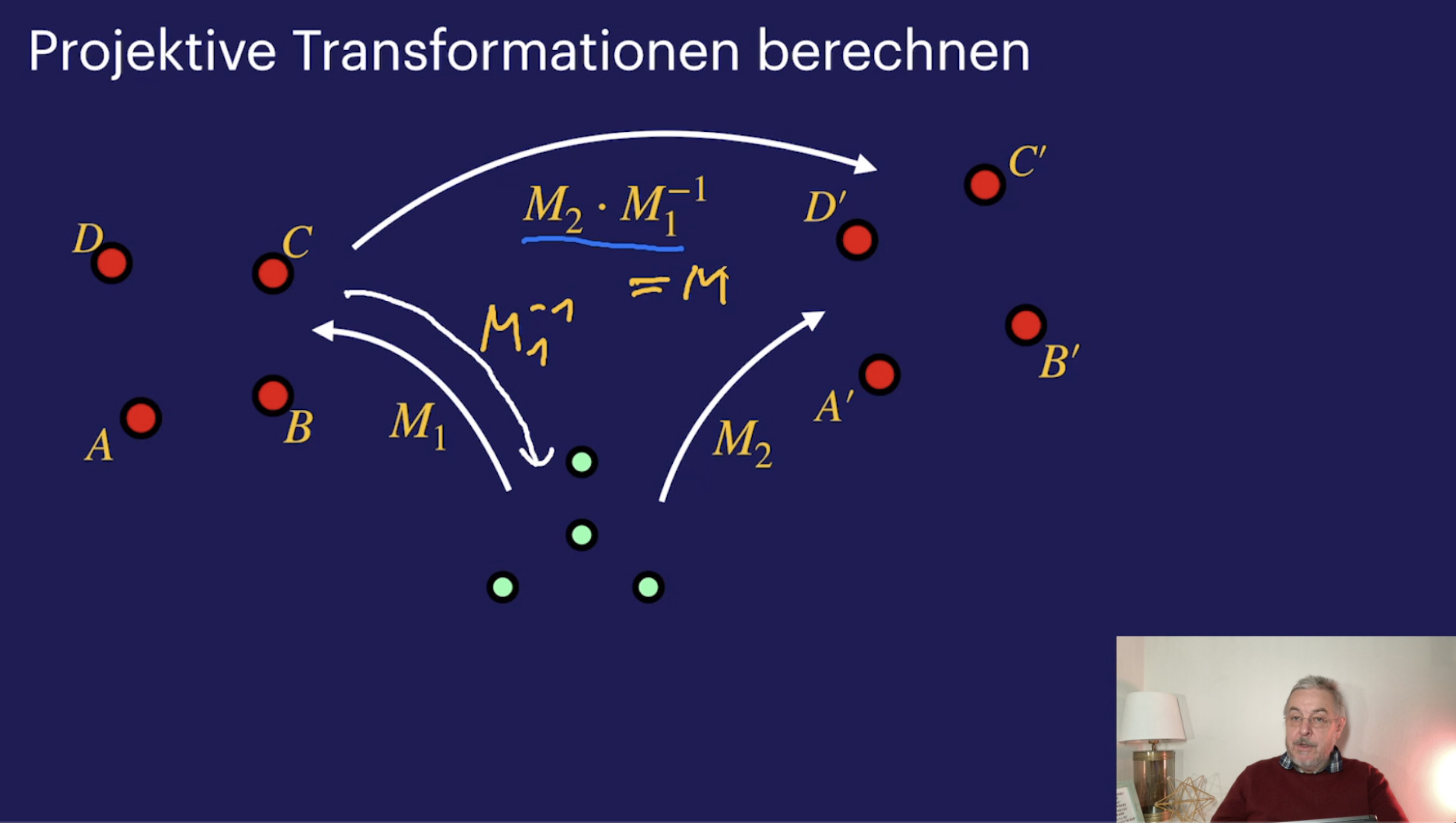
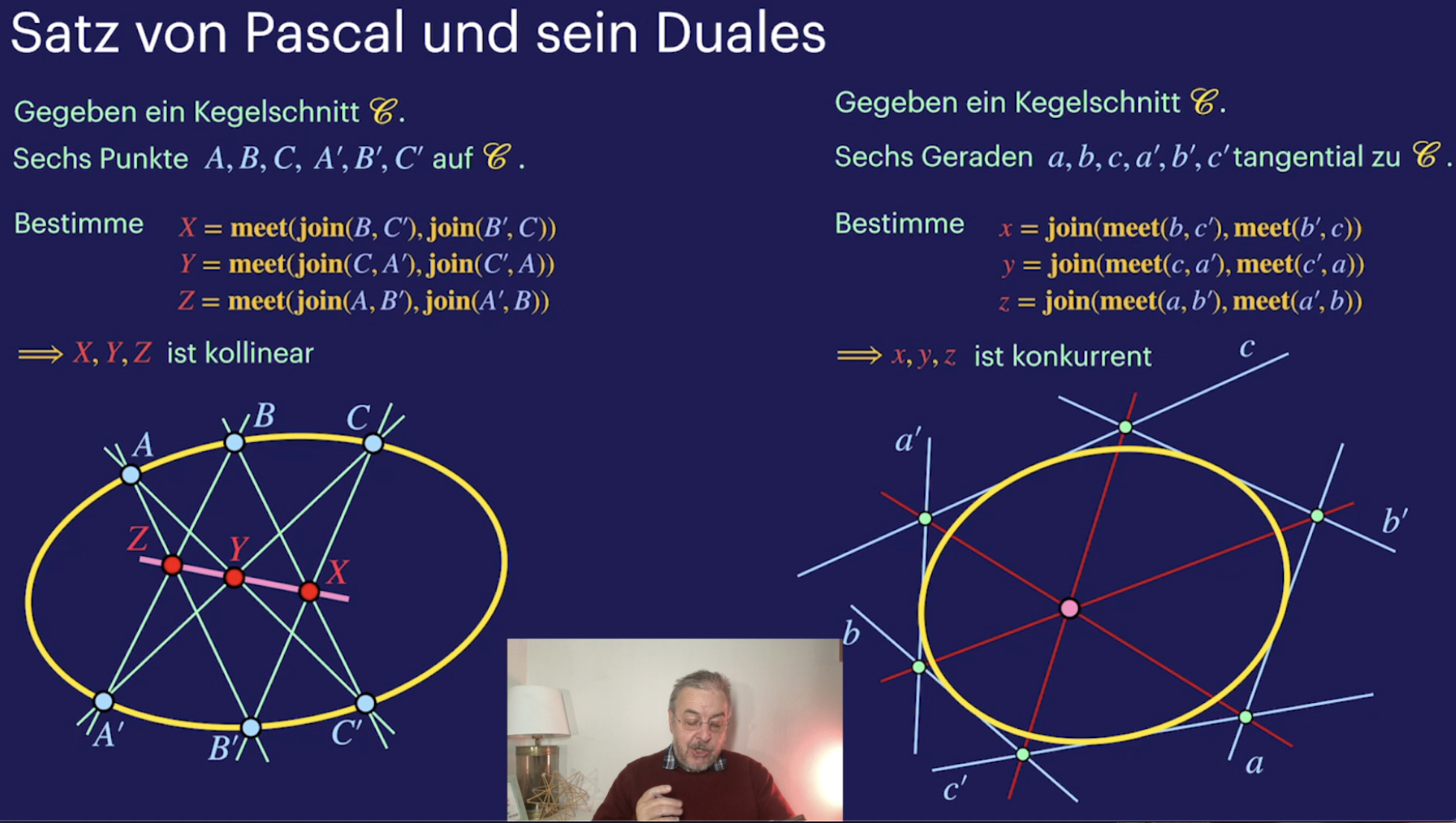
Exkurs Raumformen (33:43)
Projektive Transformationen (30:44)
Projektive Transformationen berechnen (26:05)
Dualität (22:58)
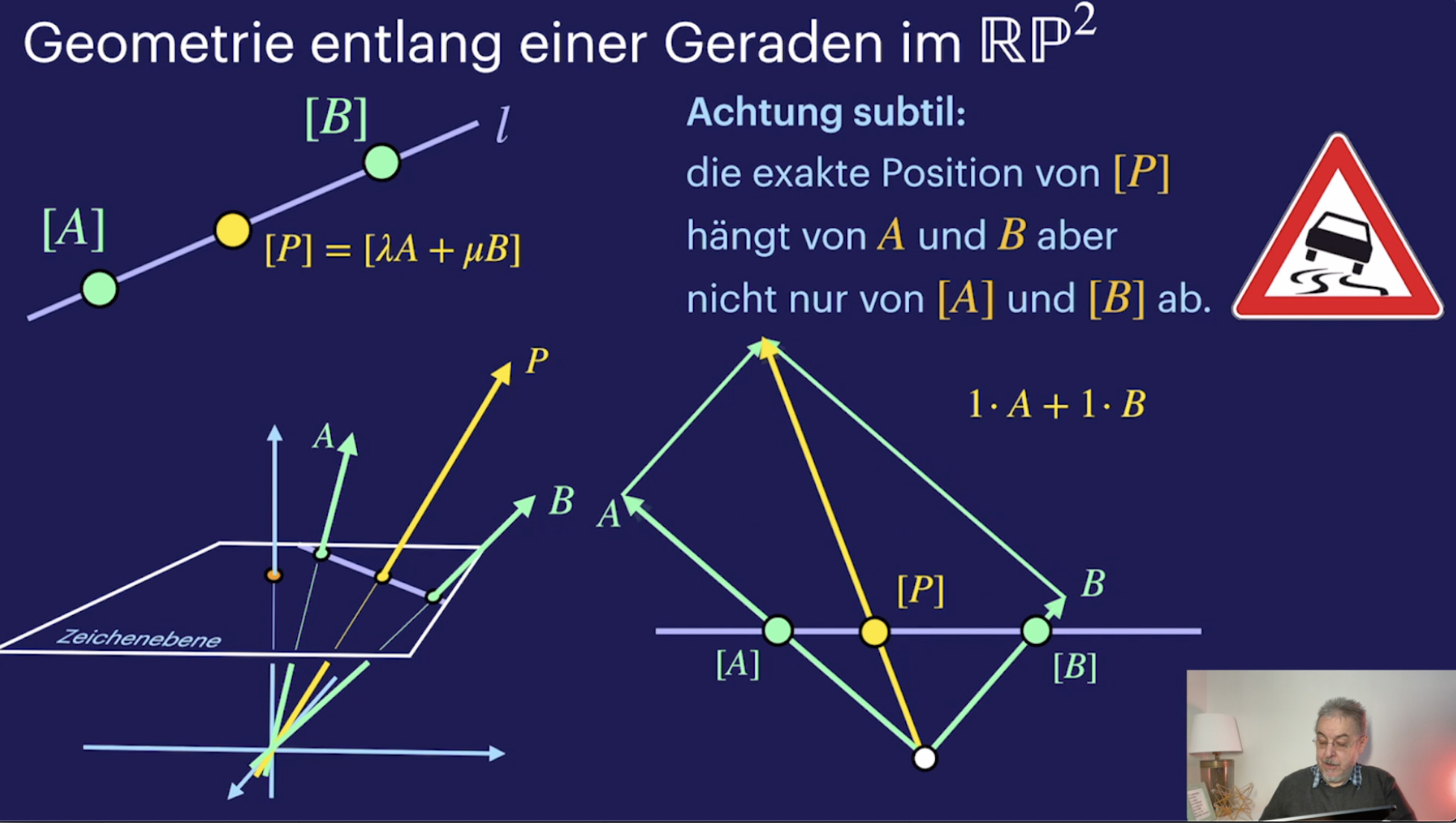
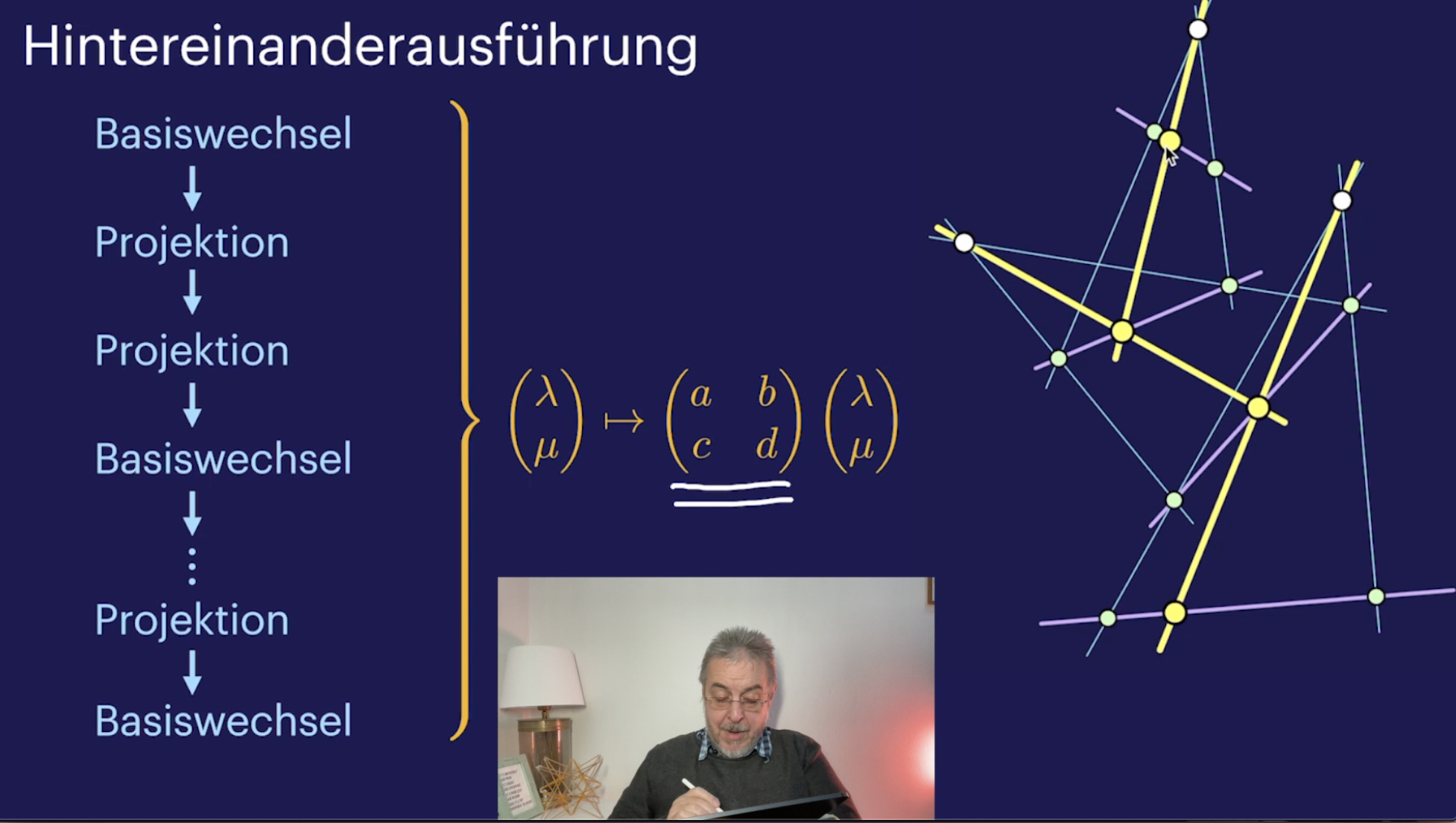
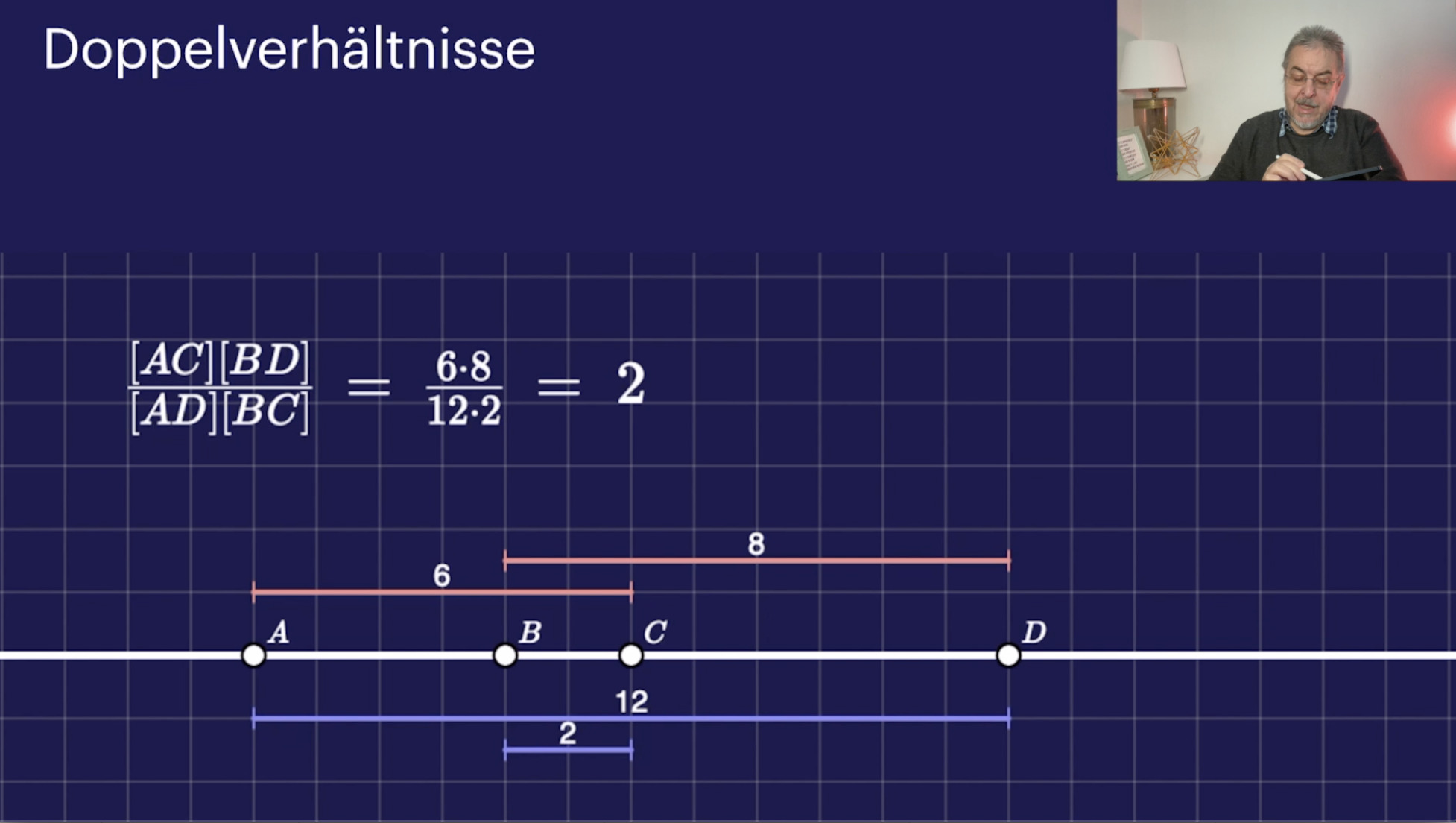
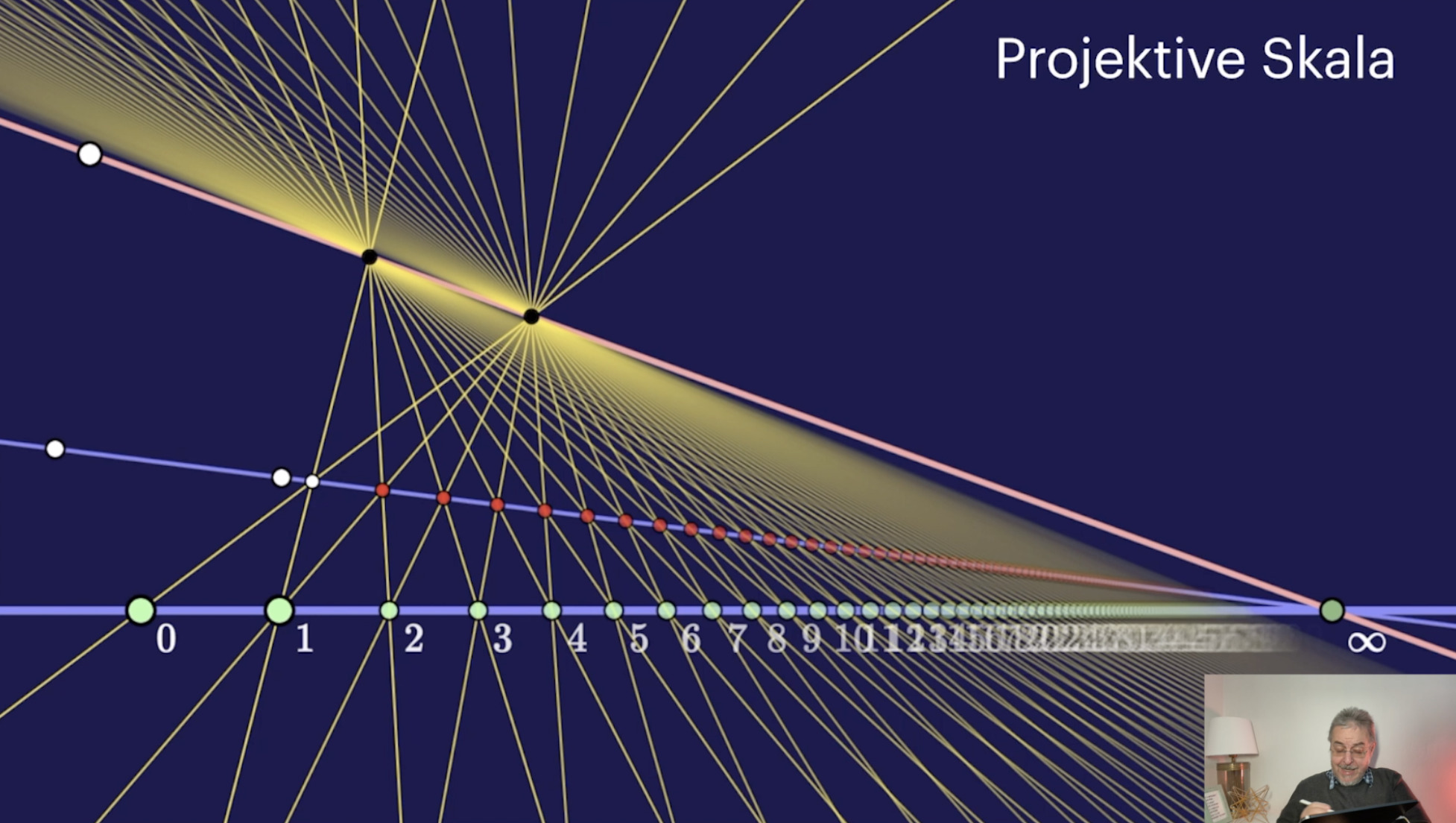
Die Projektive Gerade (13:44)
Transformationen in RP1 (24:24)
Doppelverhältnisse (27:23)
Projektive Skalen (23:27)
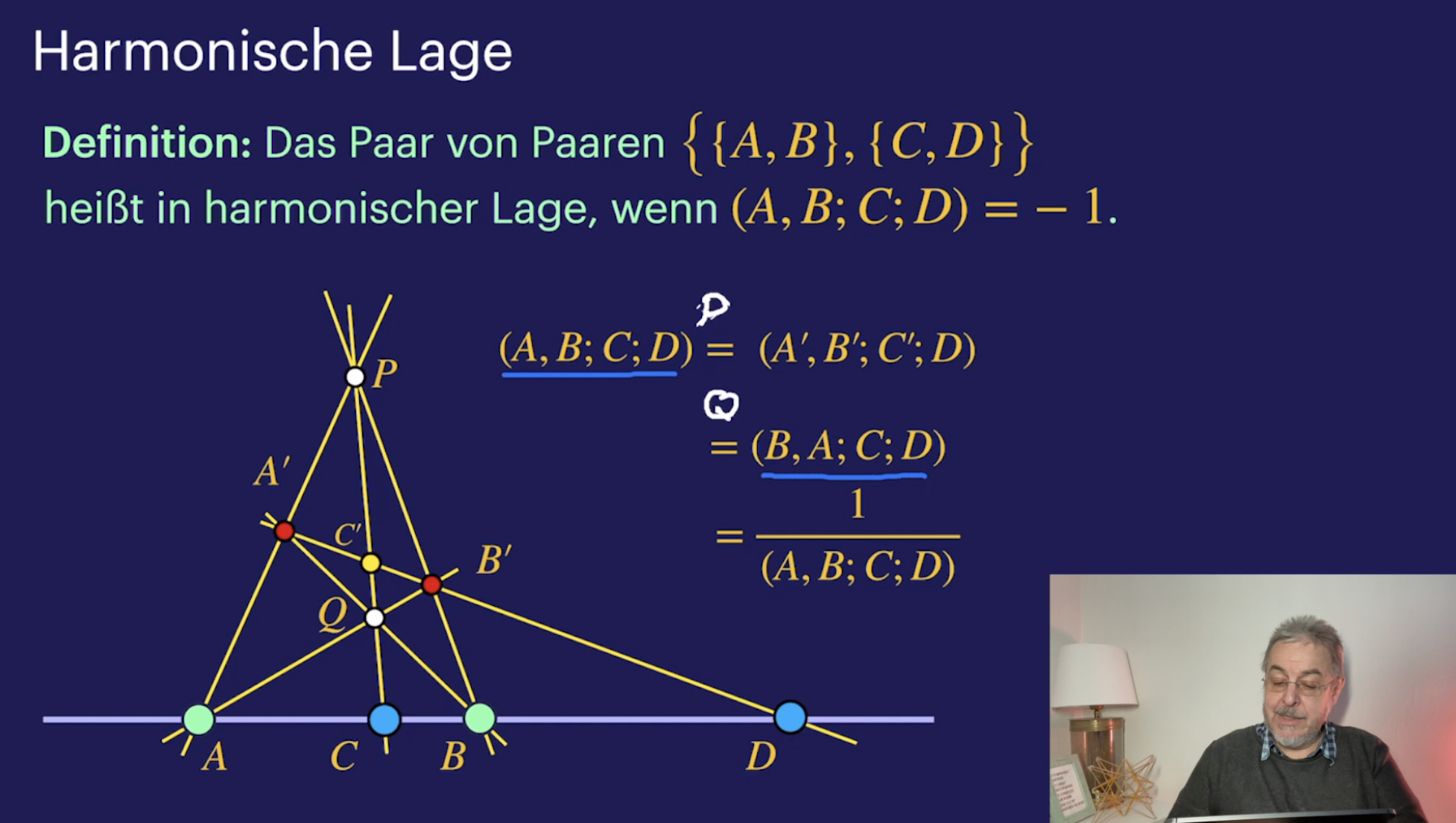
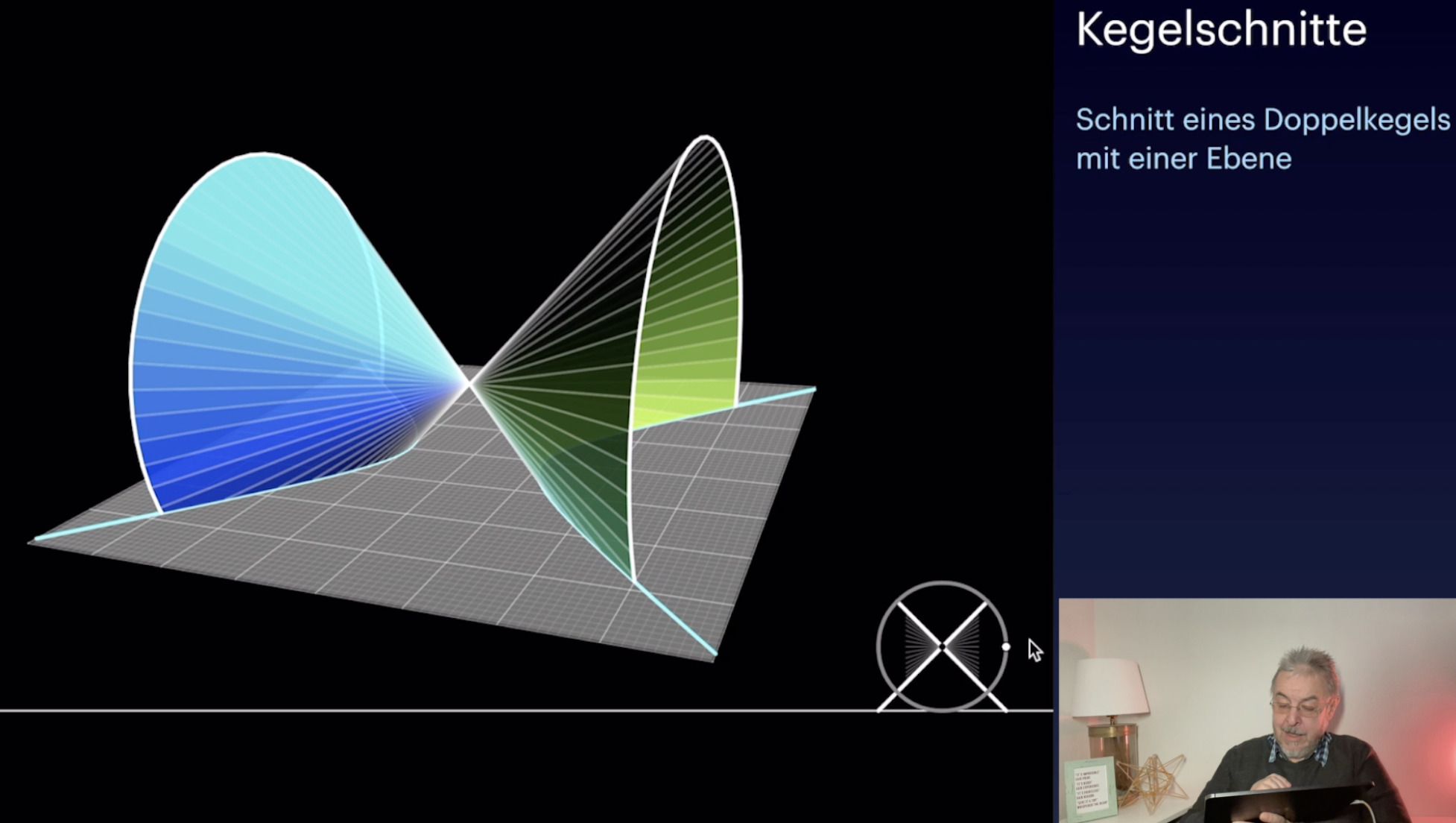

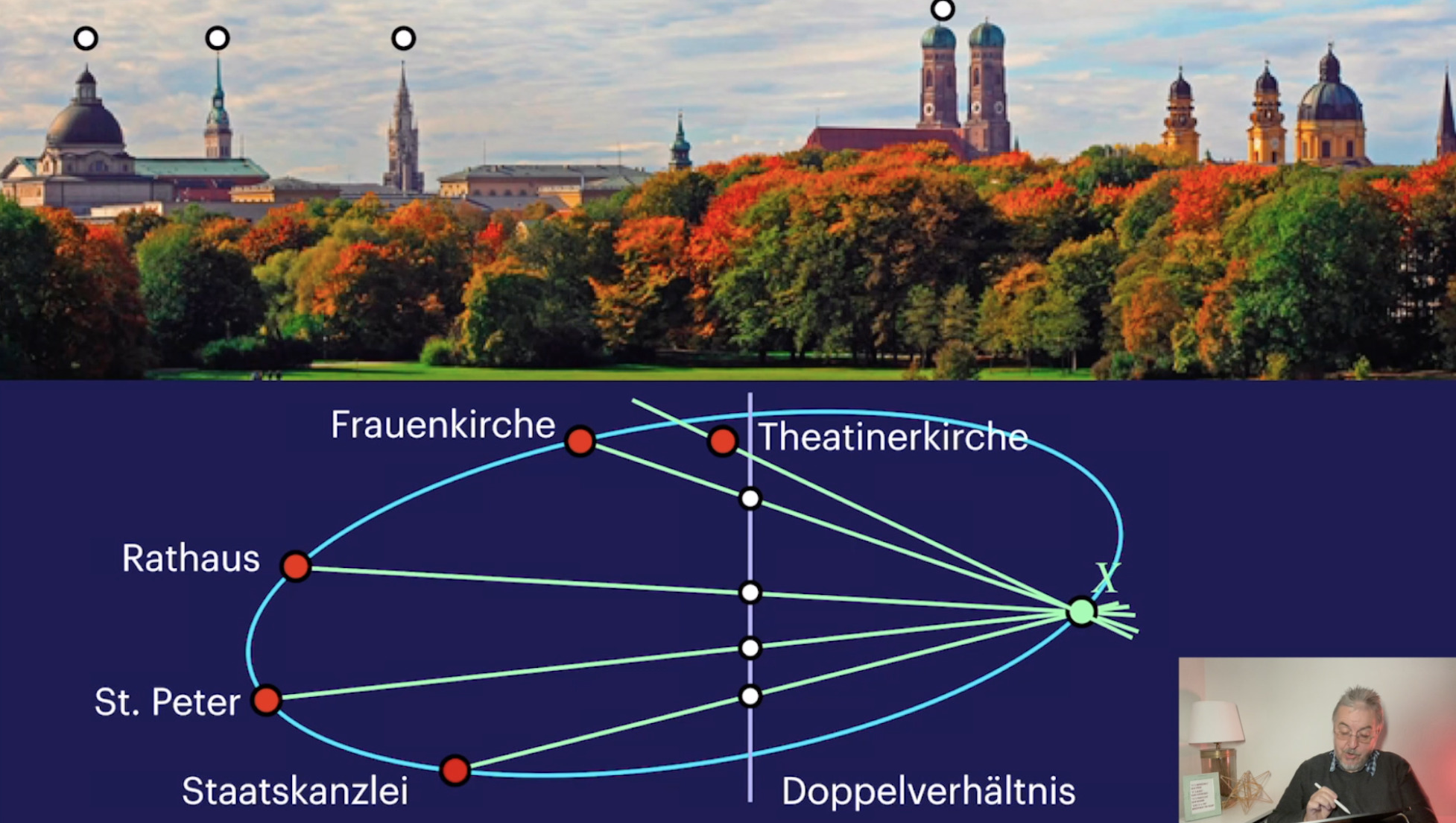
Harmonische Lage (19:56)
Quadriken (12:56)
Kegelschnitt durch 5 Punkte (26:24)
Wo stand der Fotograph (14:39)
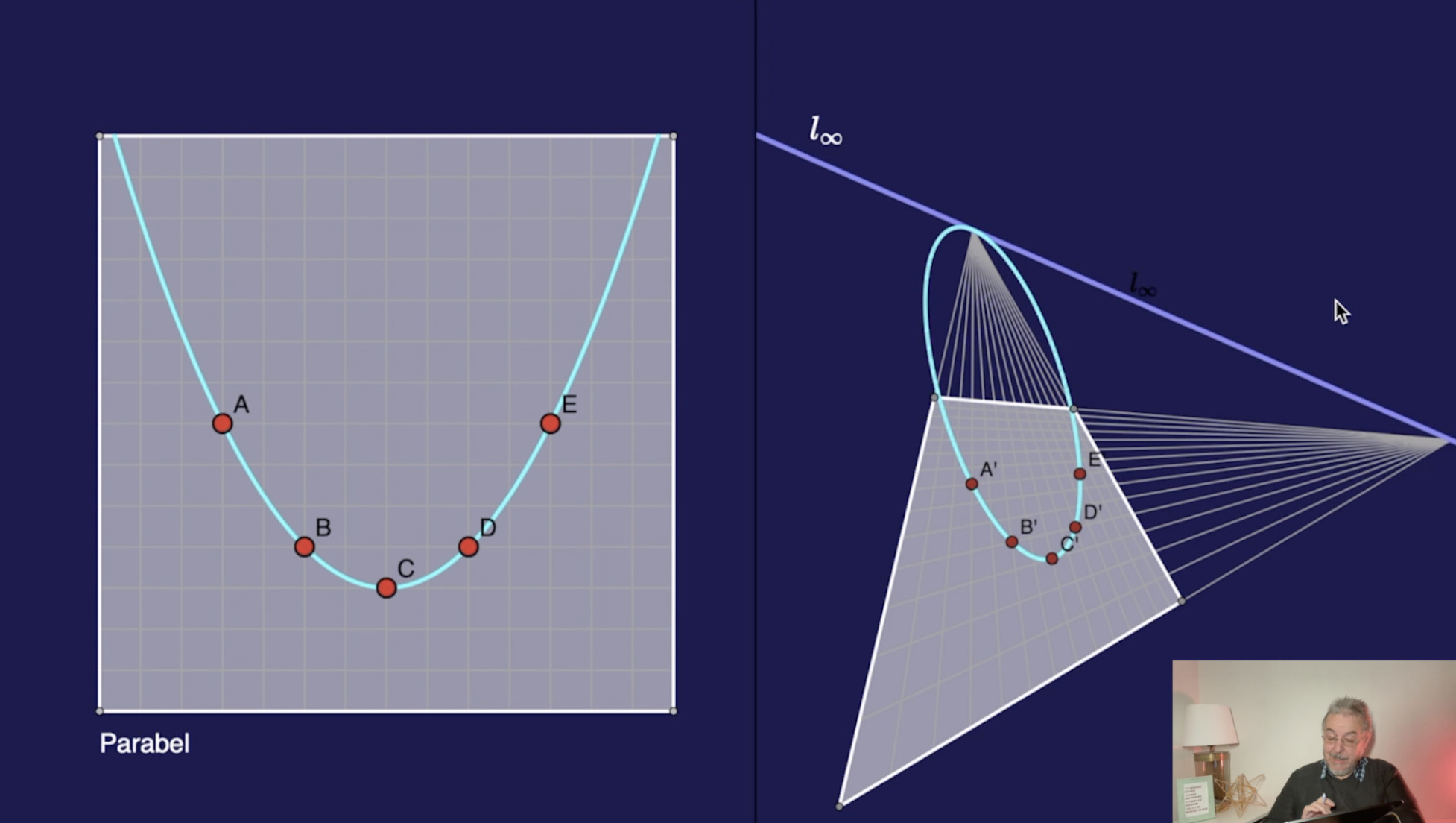
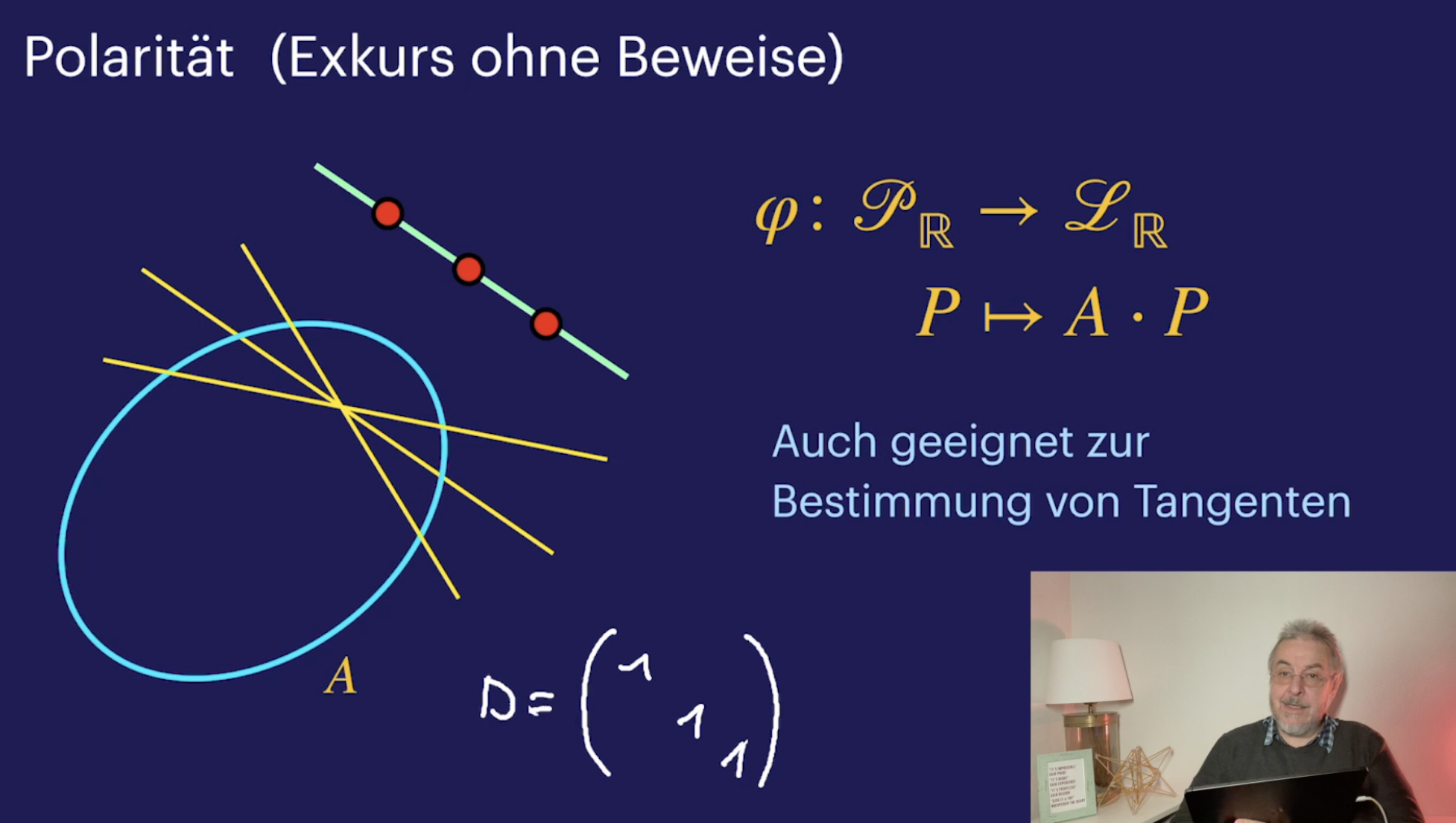
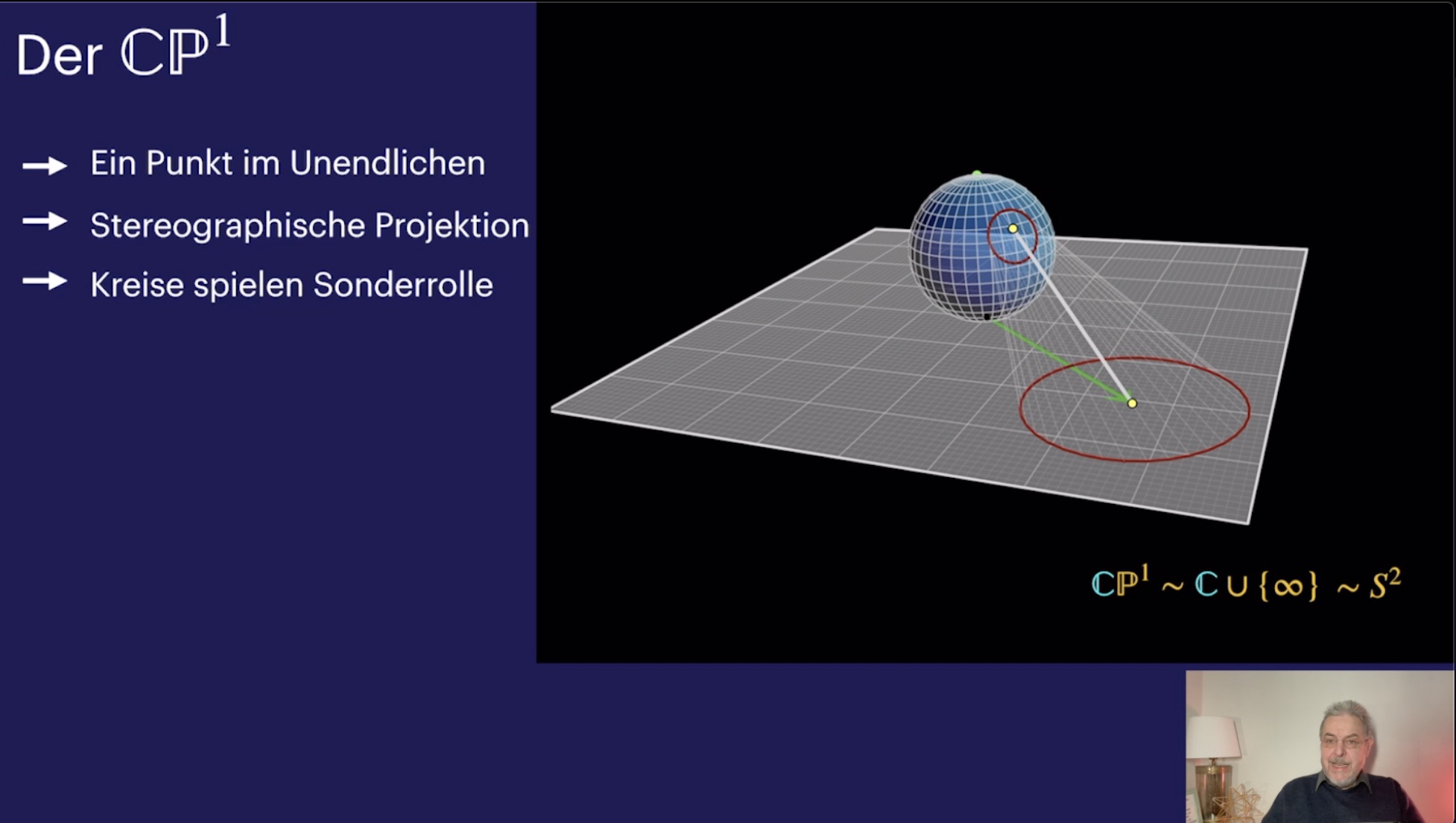
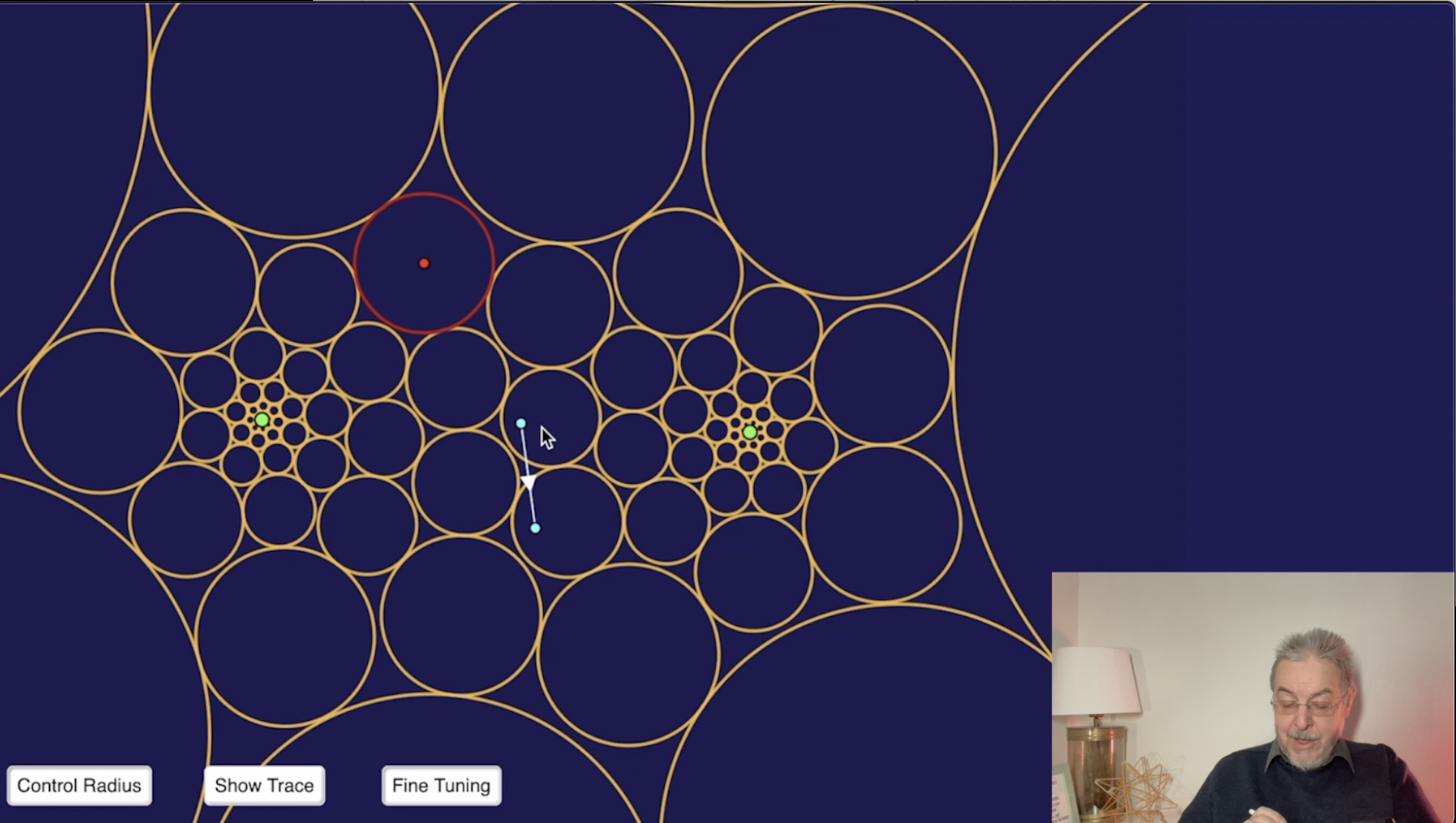
Projektive Klassifikation von Quadriken (26:08)
Polarität (8:34)
Geometrie komplexer Zahlen (24:34)
Geometrie komplexer Rechenoperationen (34:08)
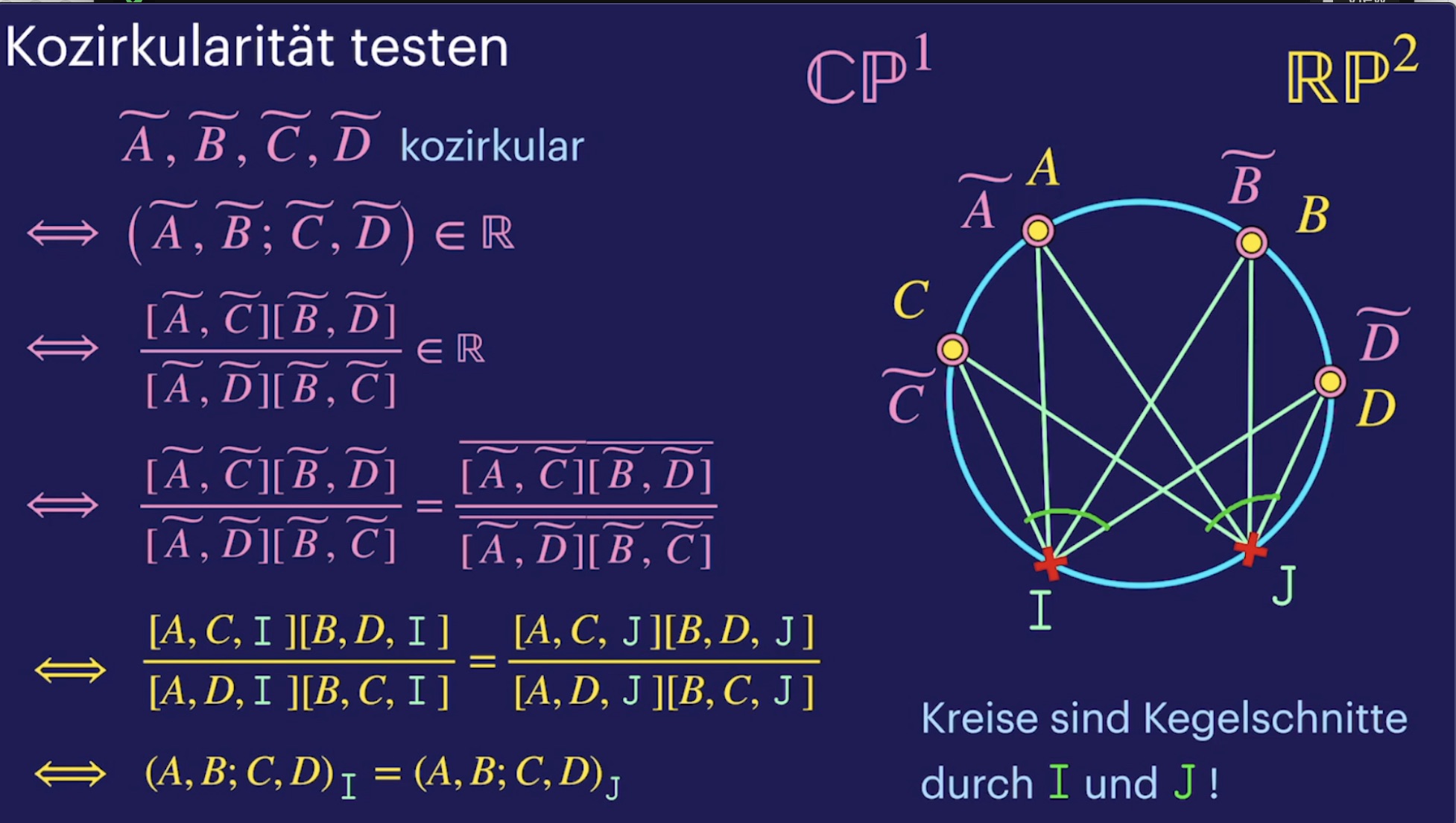
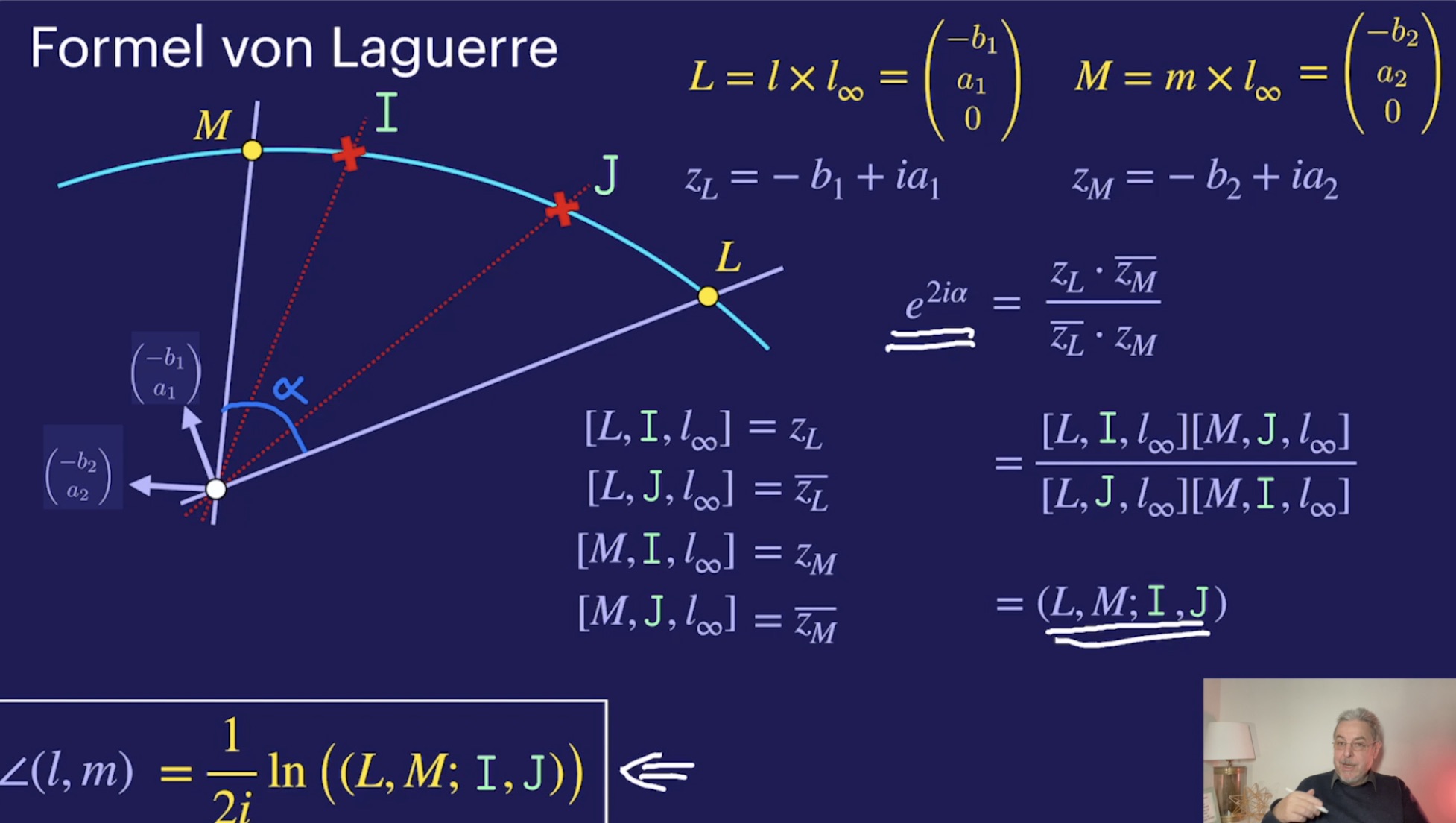
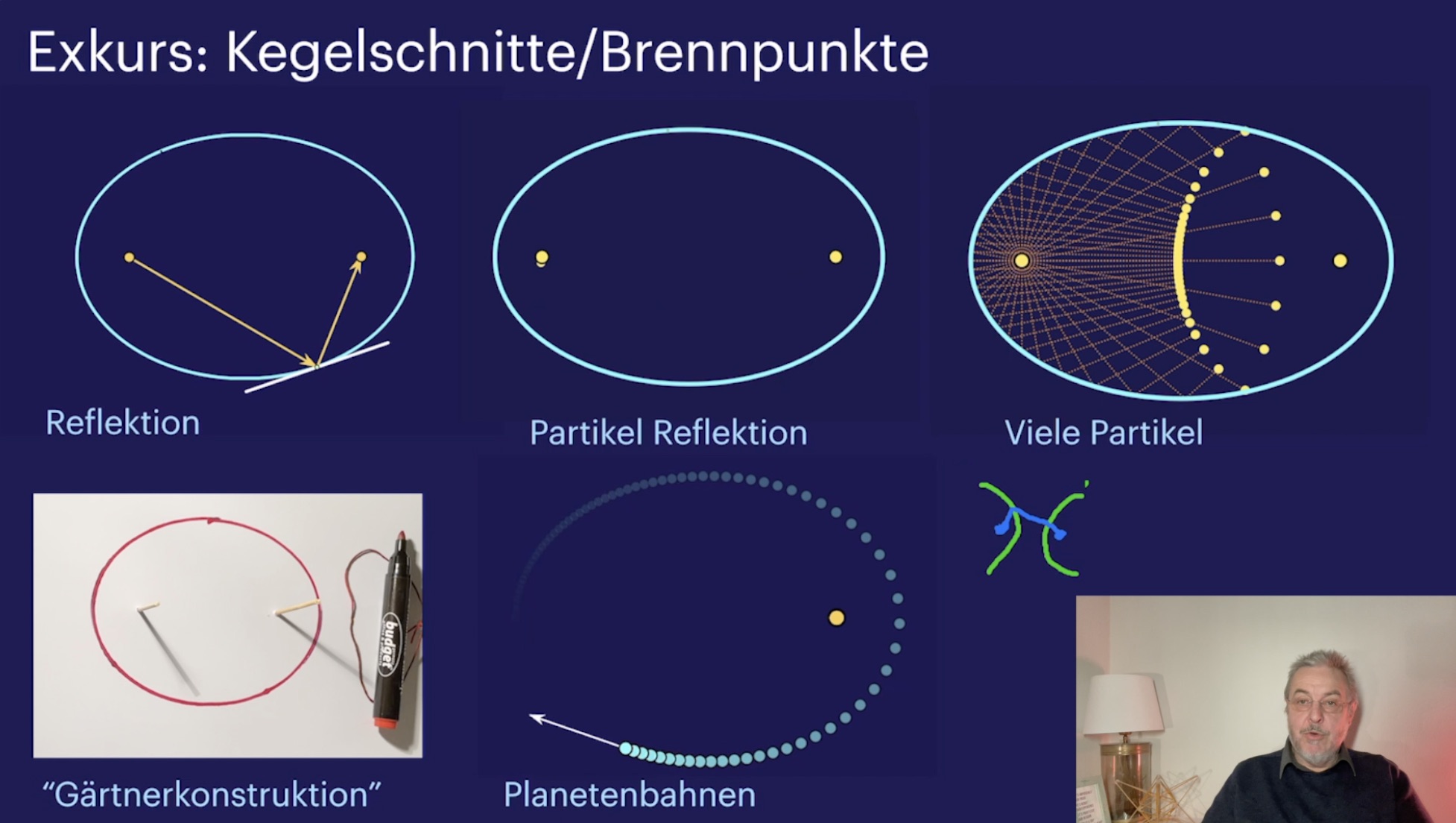
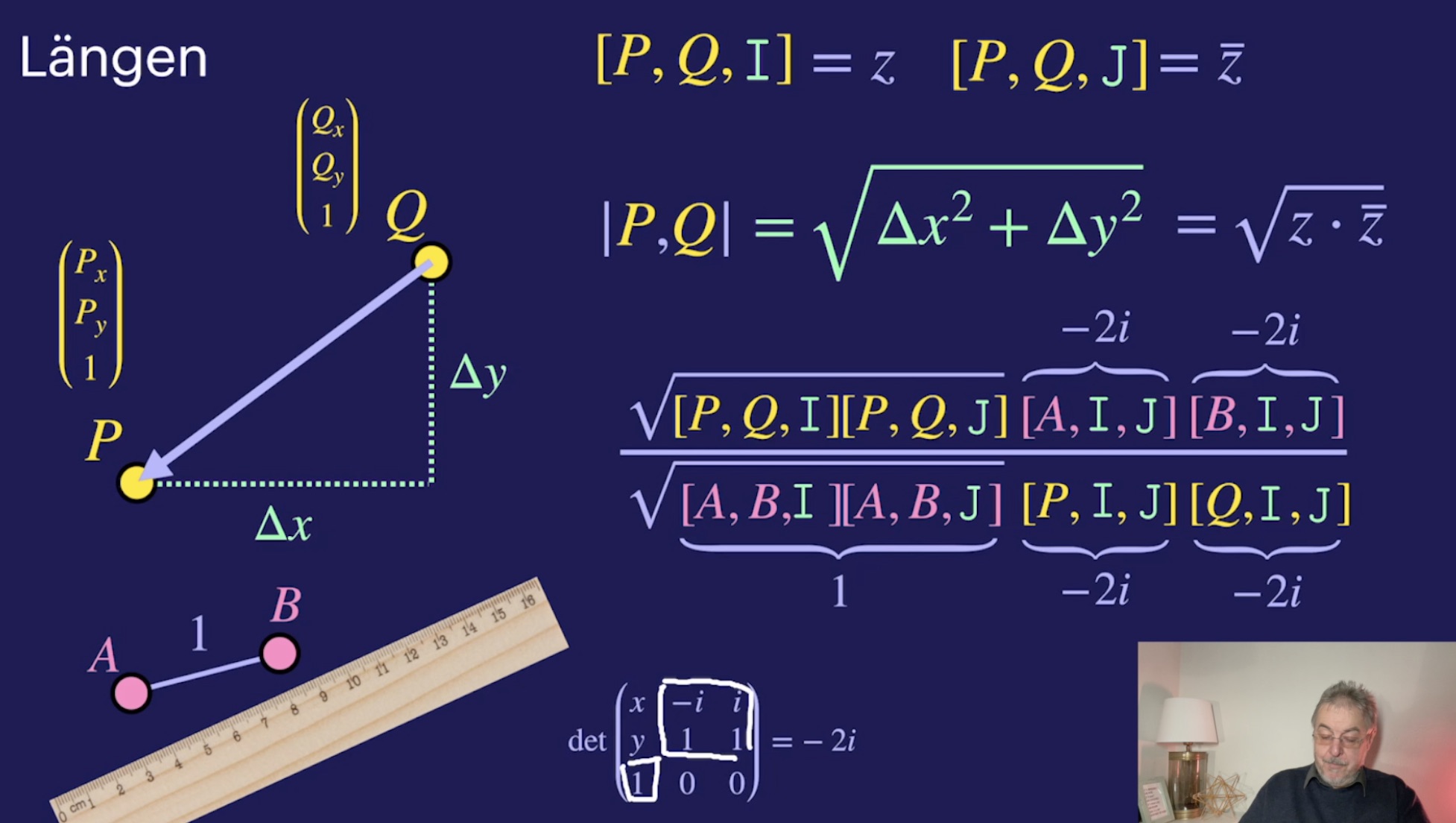
Die Punkte I und J (33:25)
Orthogonalität und Winkel (25:46)
Elementargeometrie (53:02)
Transformationen (42:42)


Ausblick: Cayley Klein Geometrien (35:24)
Nicht-Euklidische Geometrie (54:08)
Kombinatorische Geometrie
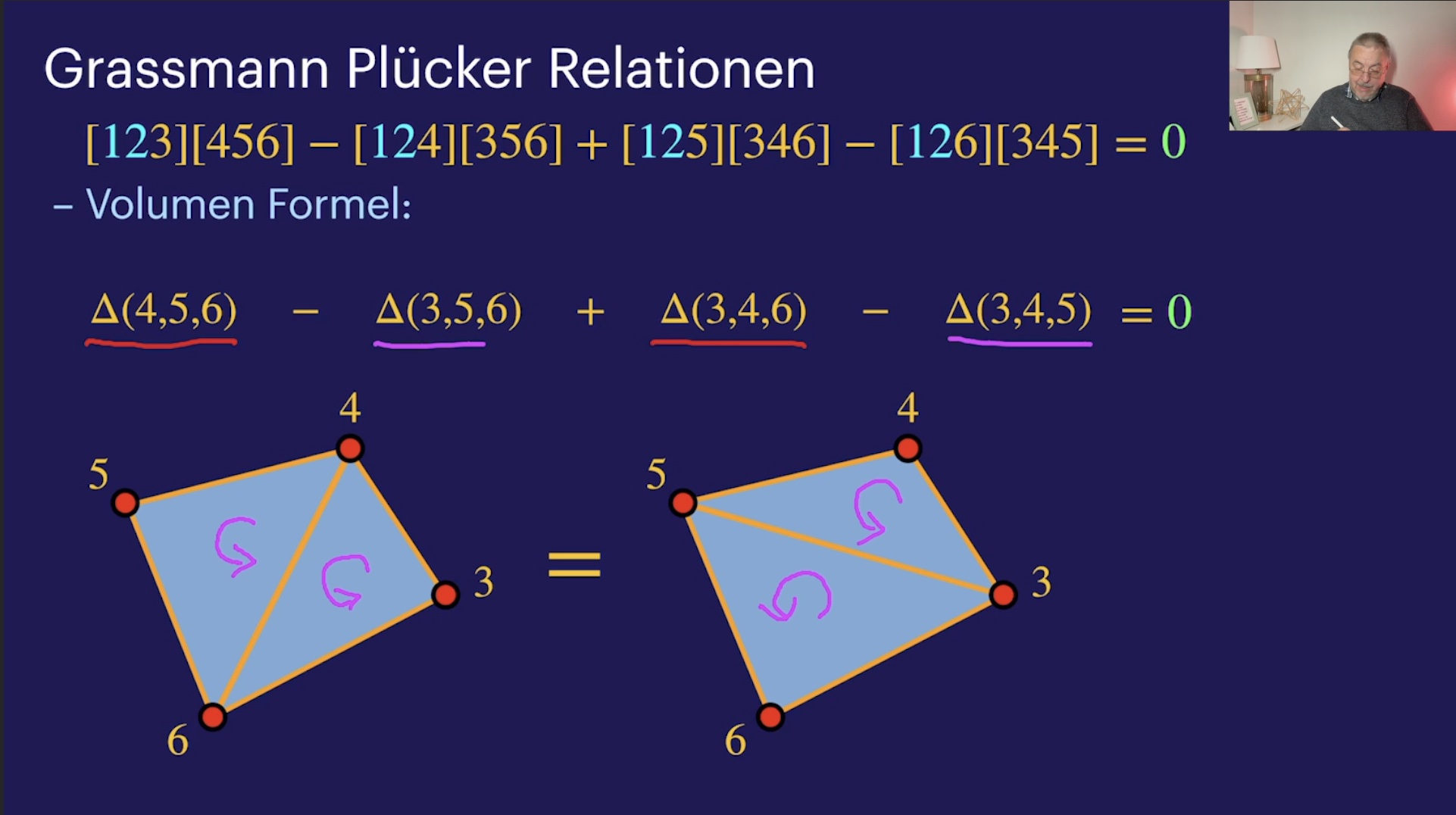
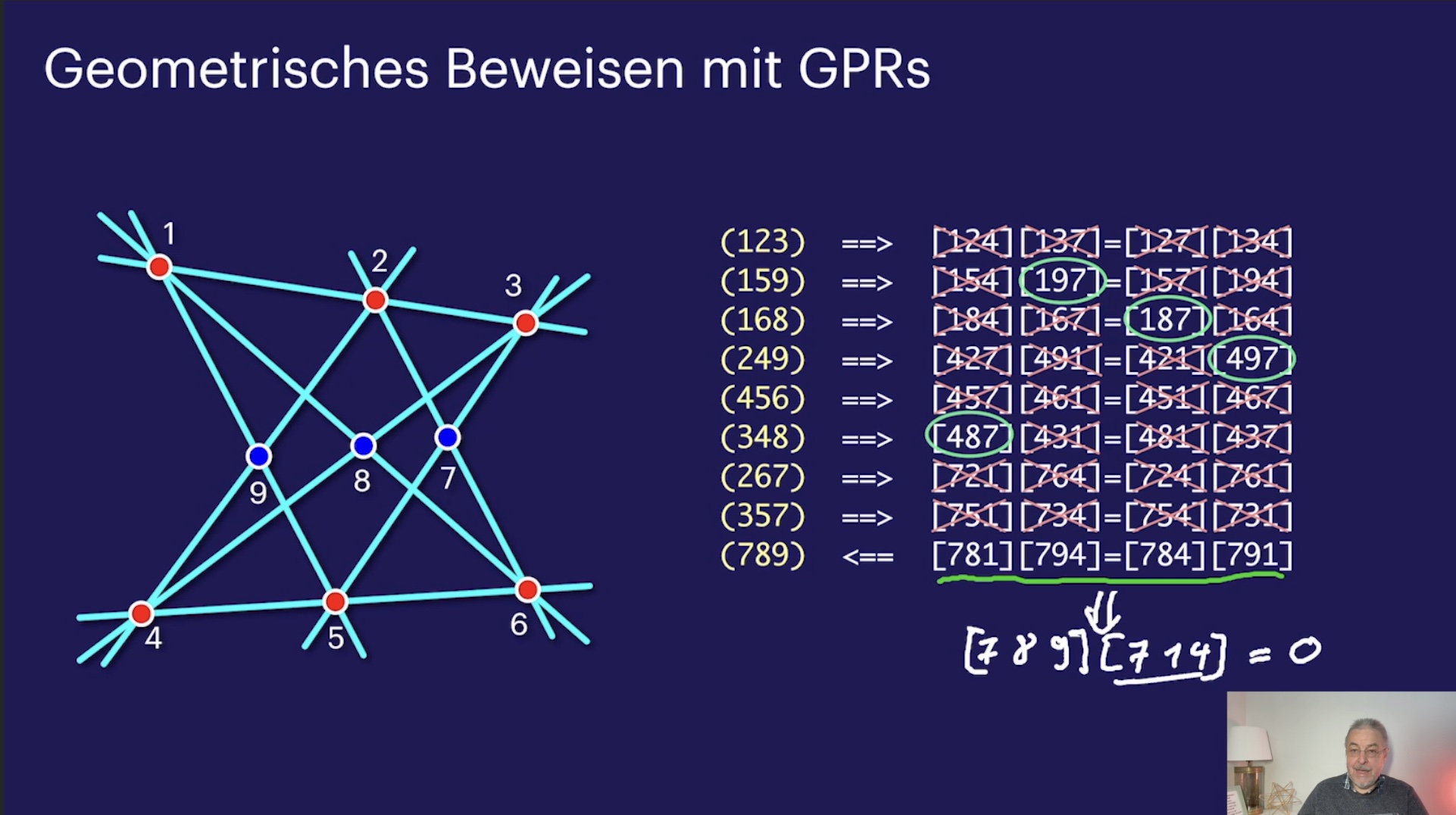


Grassmann Plücker Relationen (37:35)
Biquadratisches Beweisen (28:32)
Orientierte Matroide Einführung (11:25)
Orientierte Projektive Geometrie (34:59)
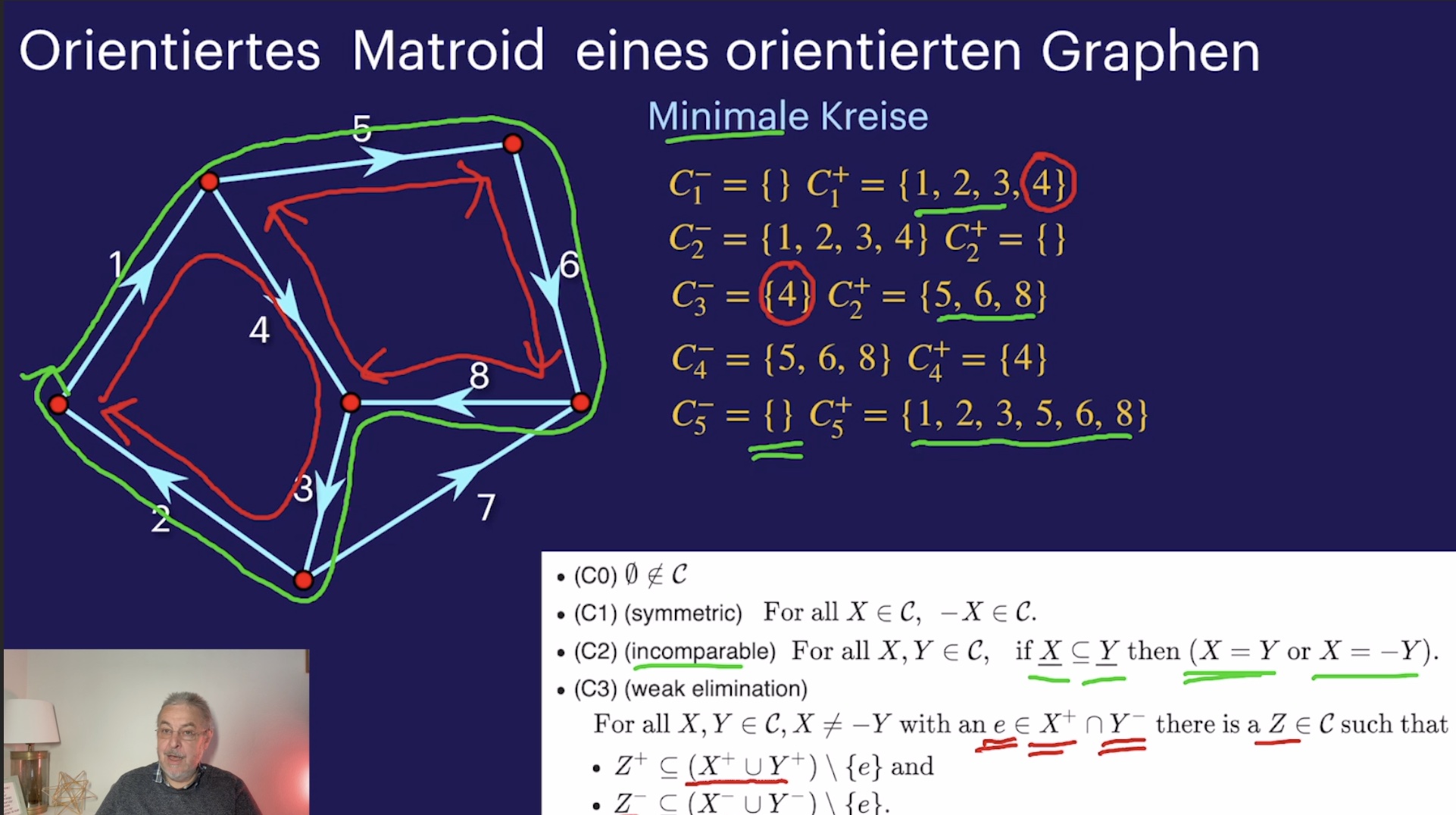

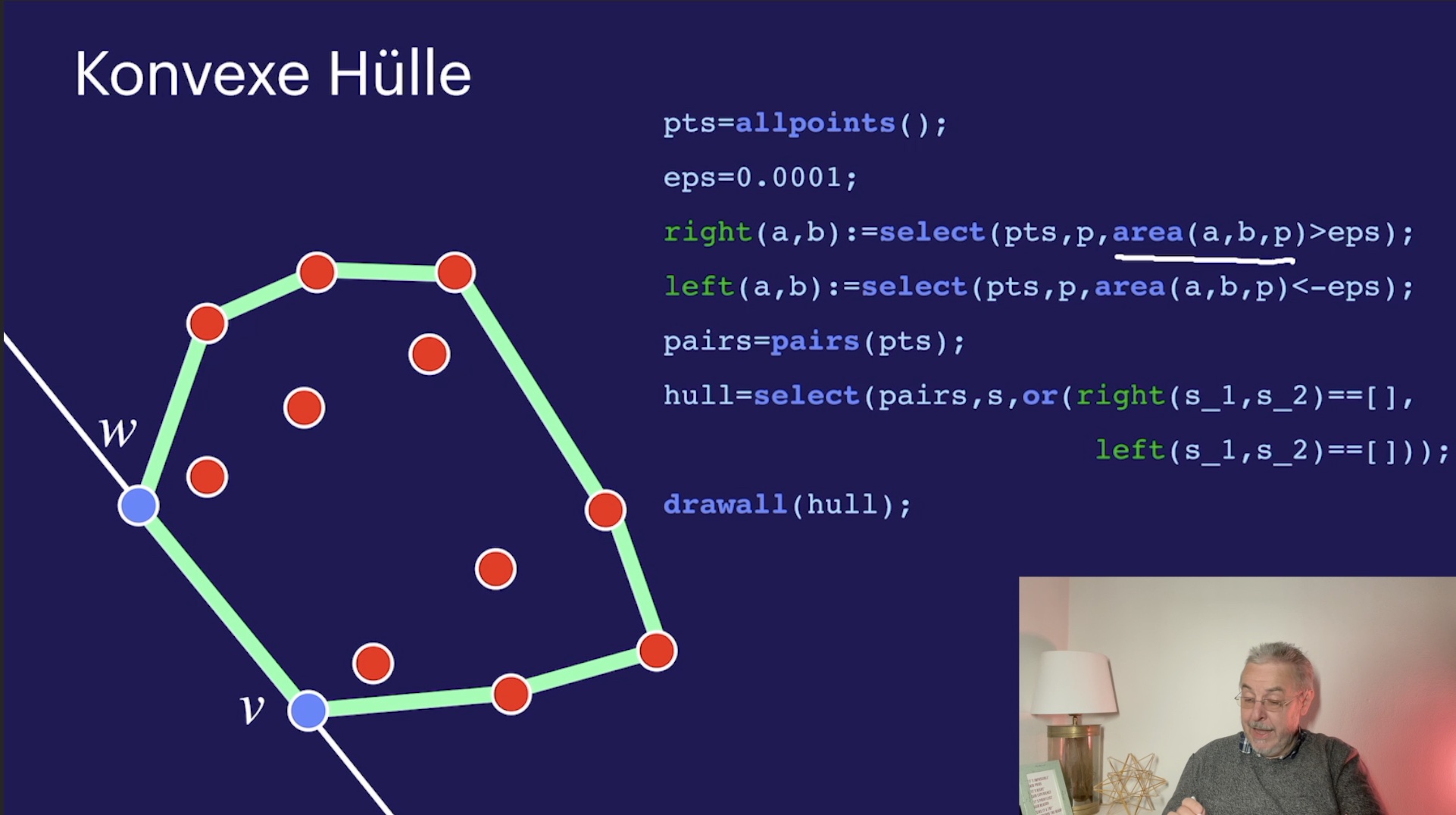

Kreise und Kokreise (49:16
Chirotope (51:41)
Einfache Algorithmen (13:42)
Lokale Realisierbarkeit (22:49)

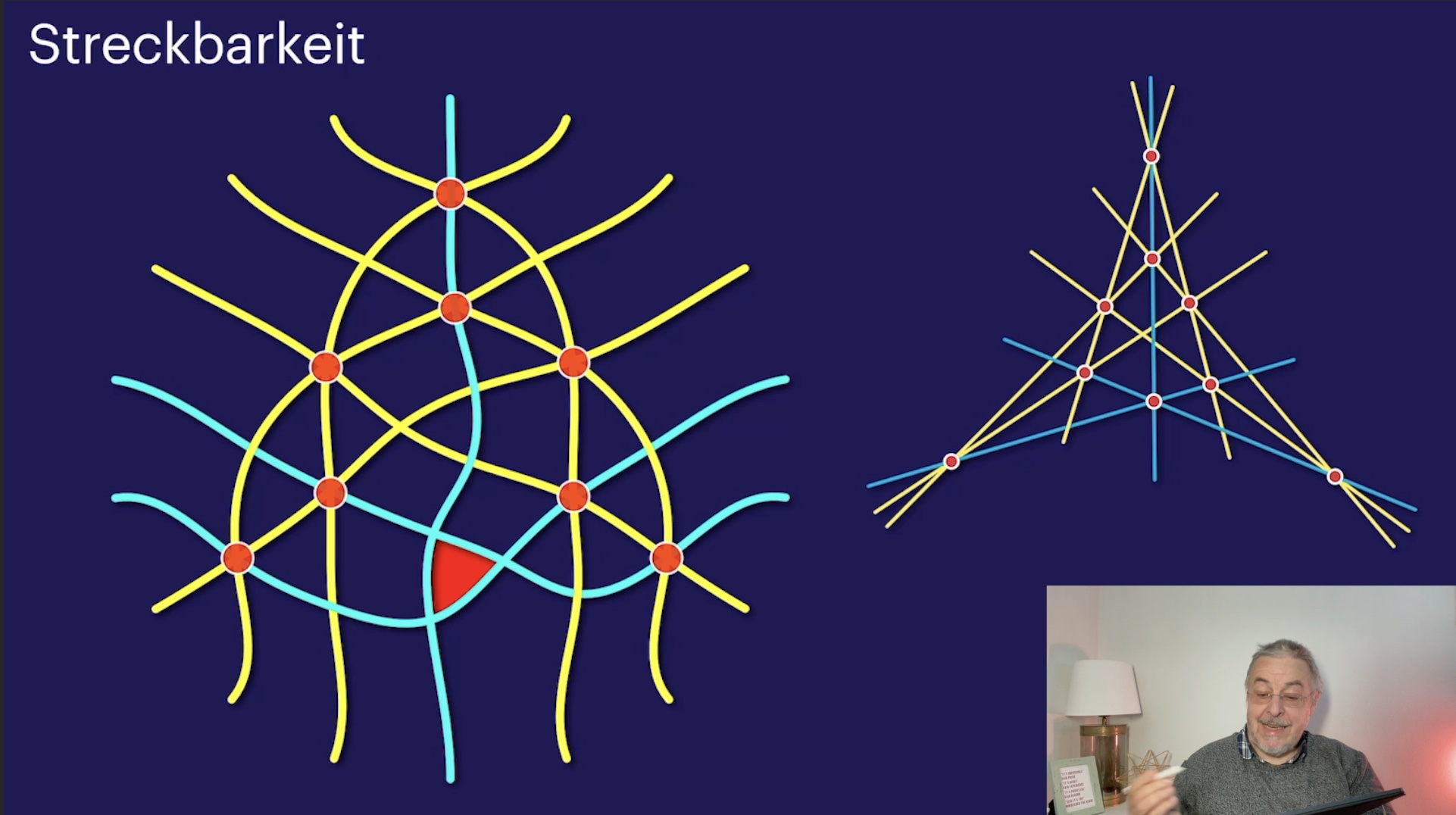
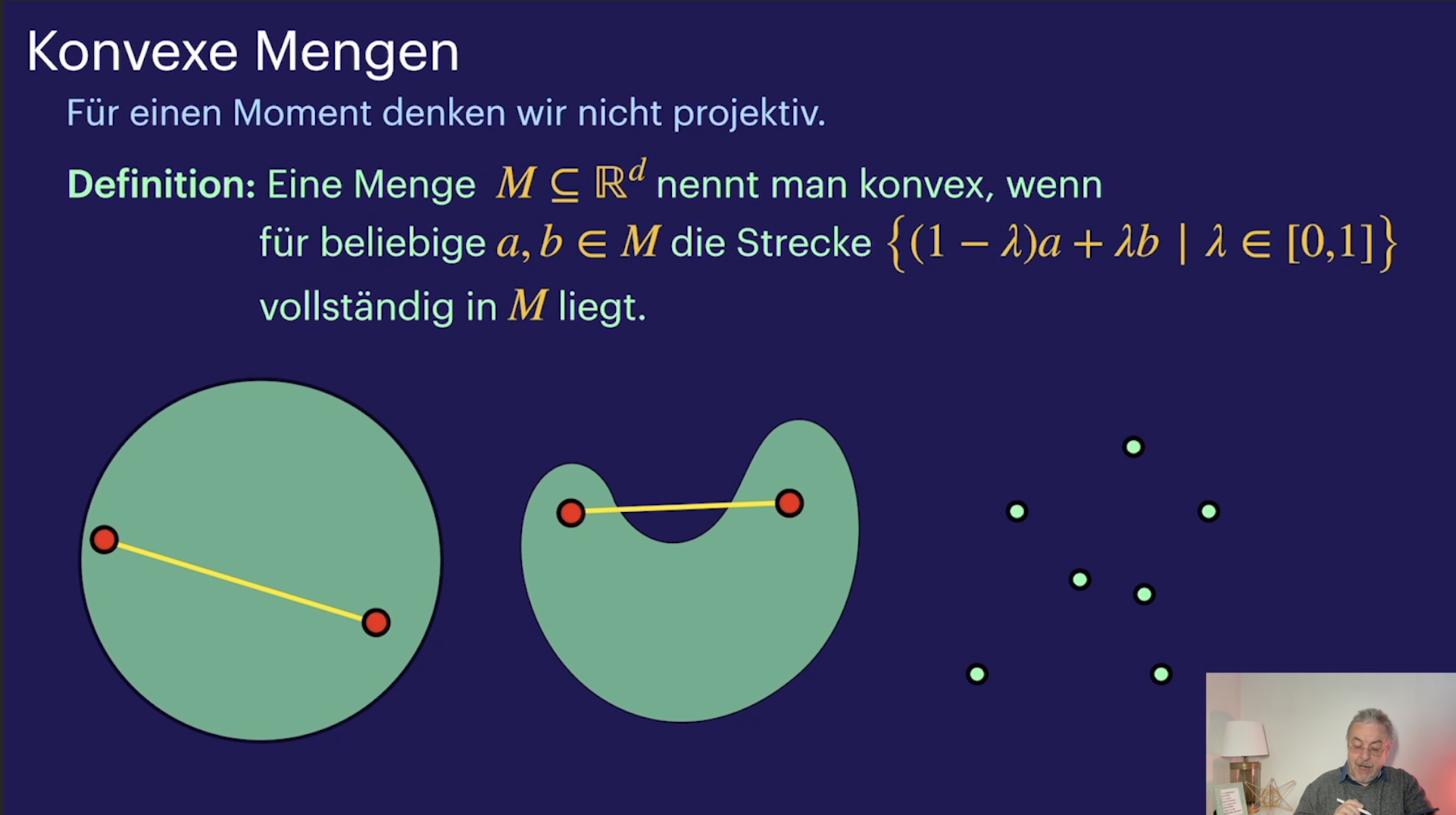

Leuchttürme und Pseudogeraden (35:38)
Streckbarkeit (26:36)
Konvexe Mengen (31:38)
Polytope (27:40)
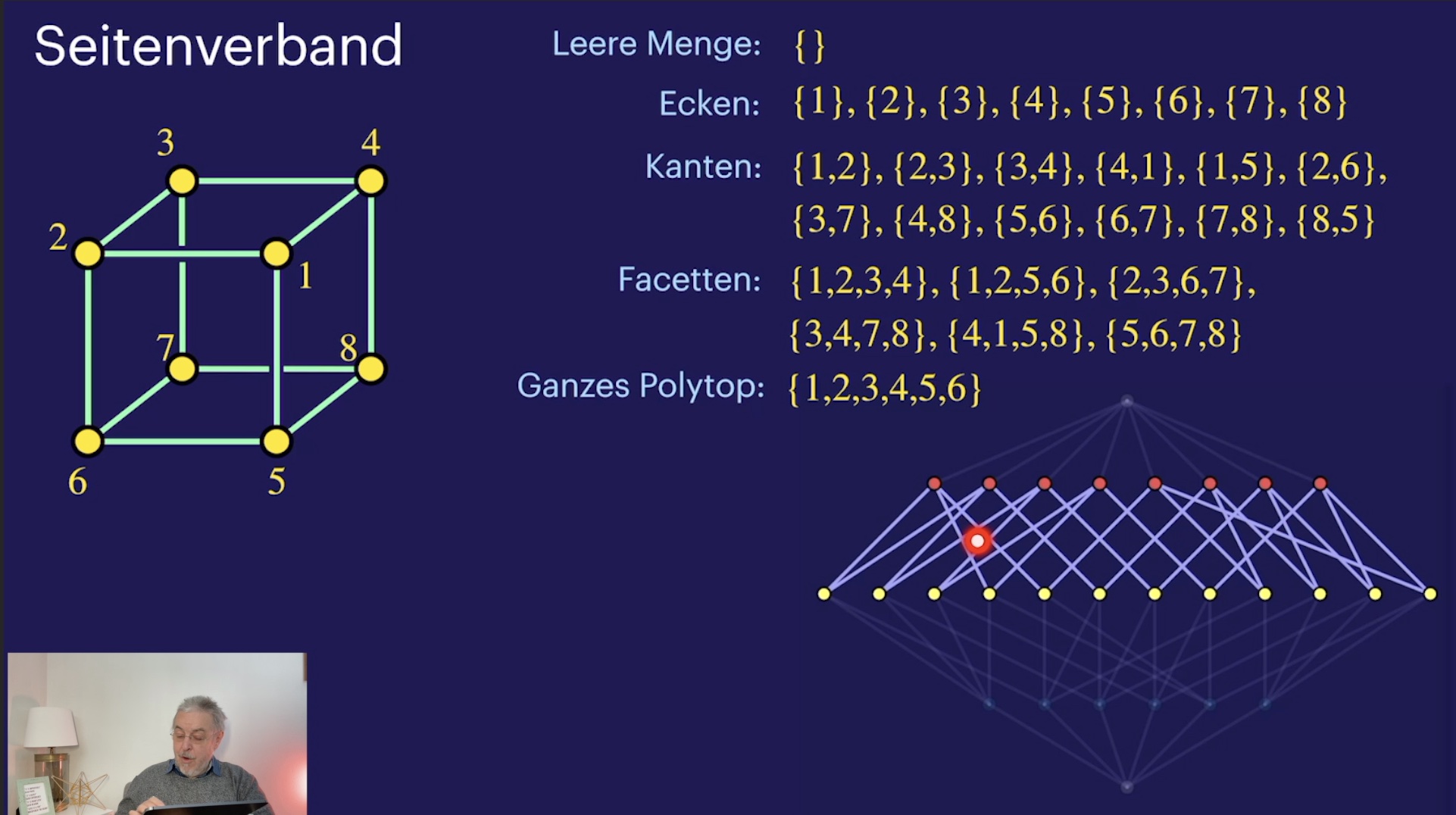
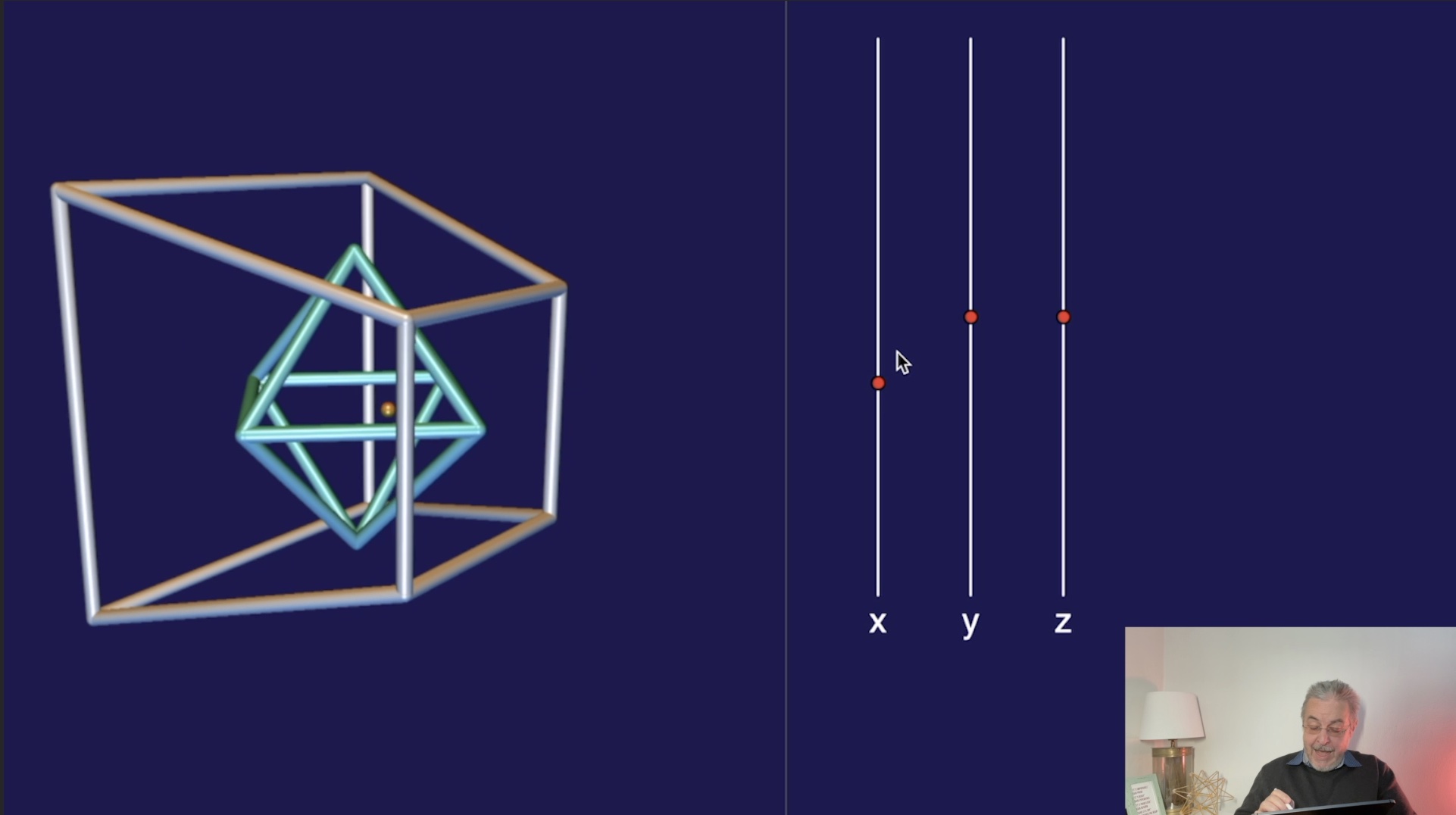
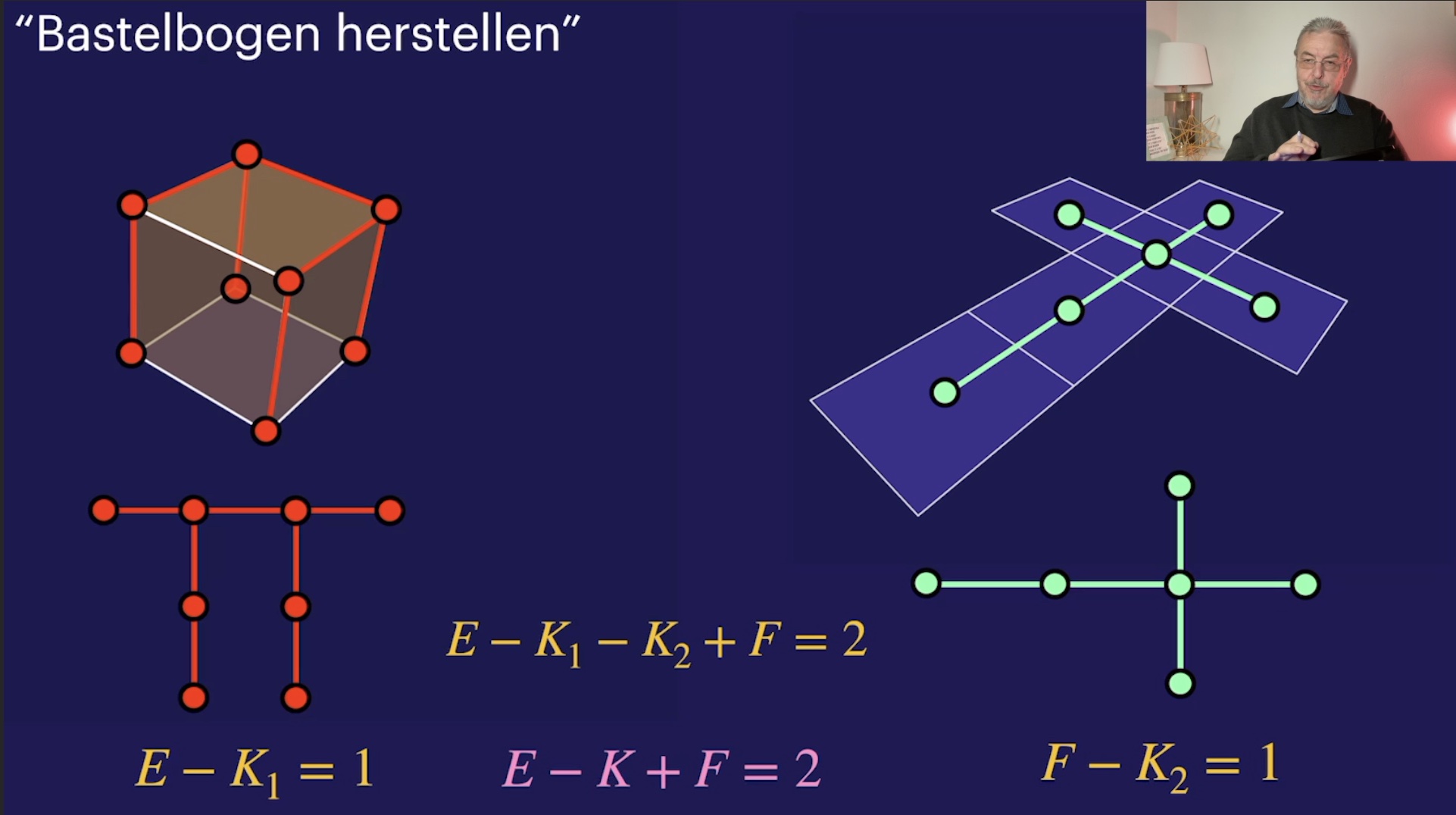

Seitenverband (28:09)
Polarität (46:34)
Euler'sche Polyederformel I (23:20)
Euler'sche Polyederformel II (34:54)
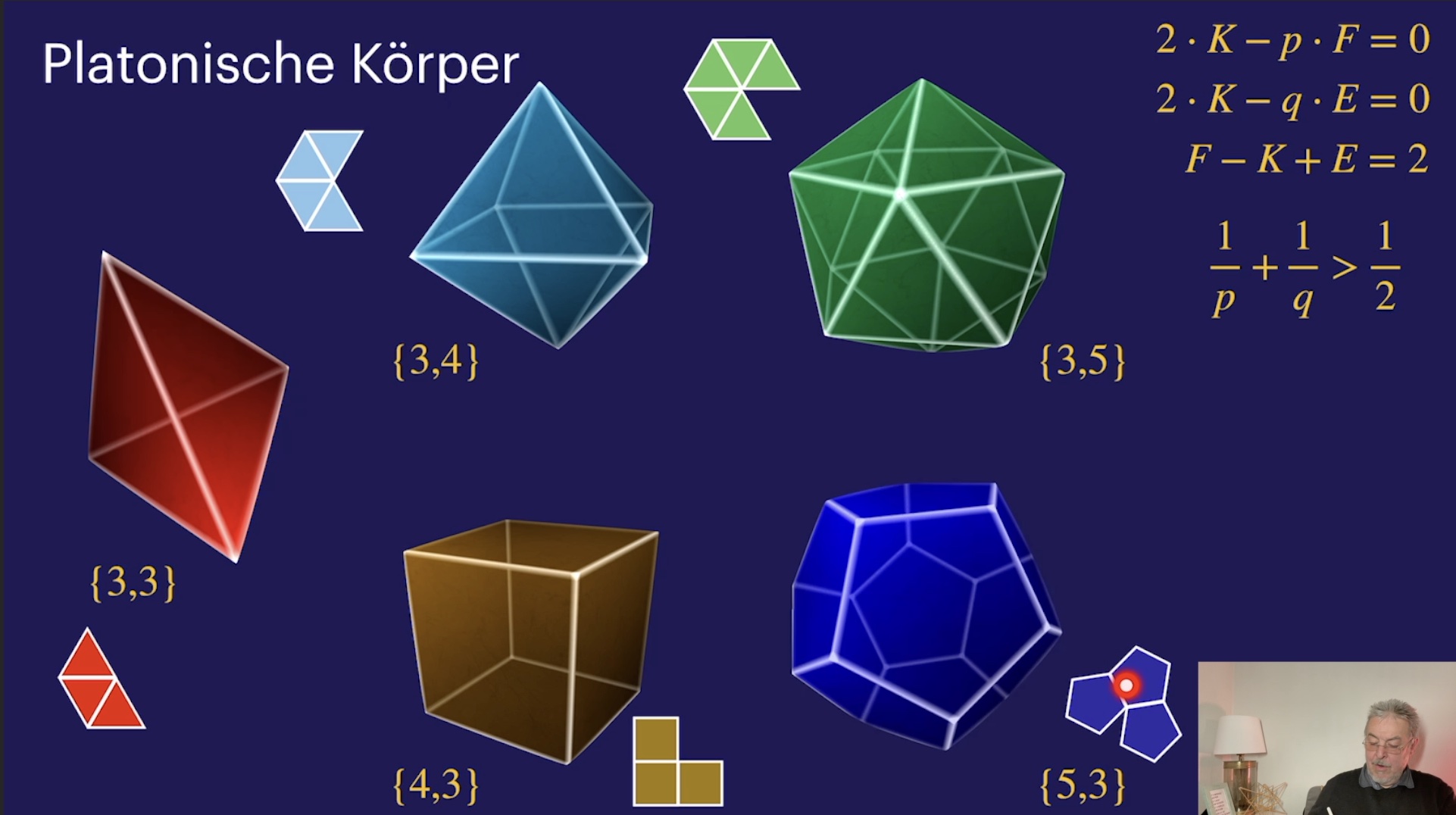
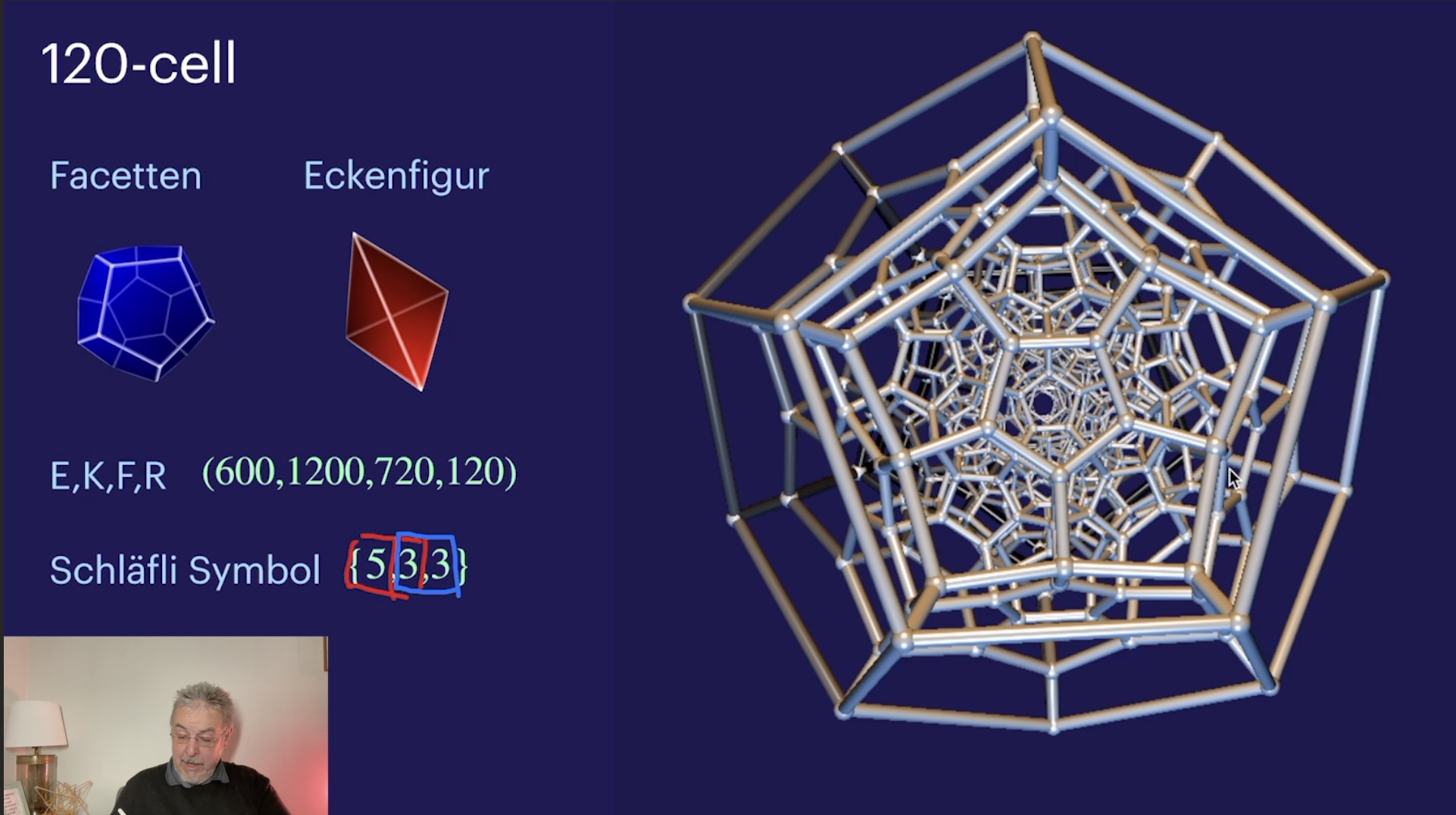
Reguläre Polytope I (40:24)
Reguläre Polytope II (38:42)
Projective Geometry

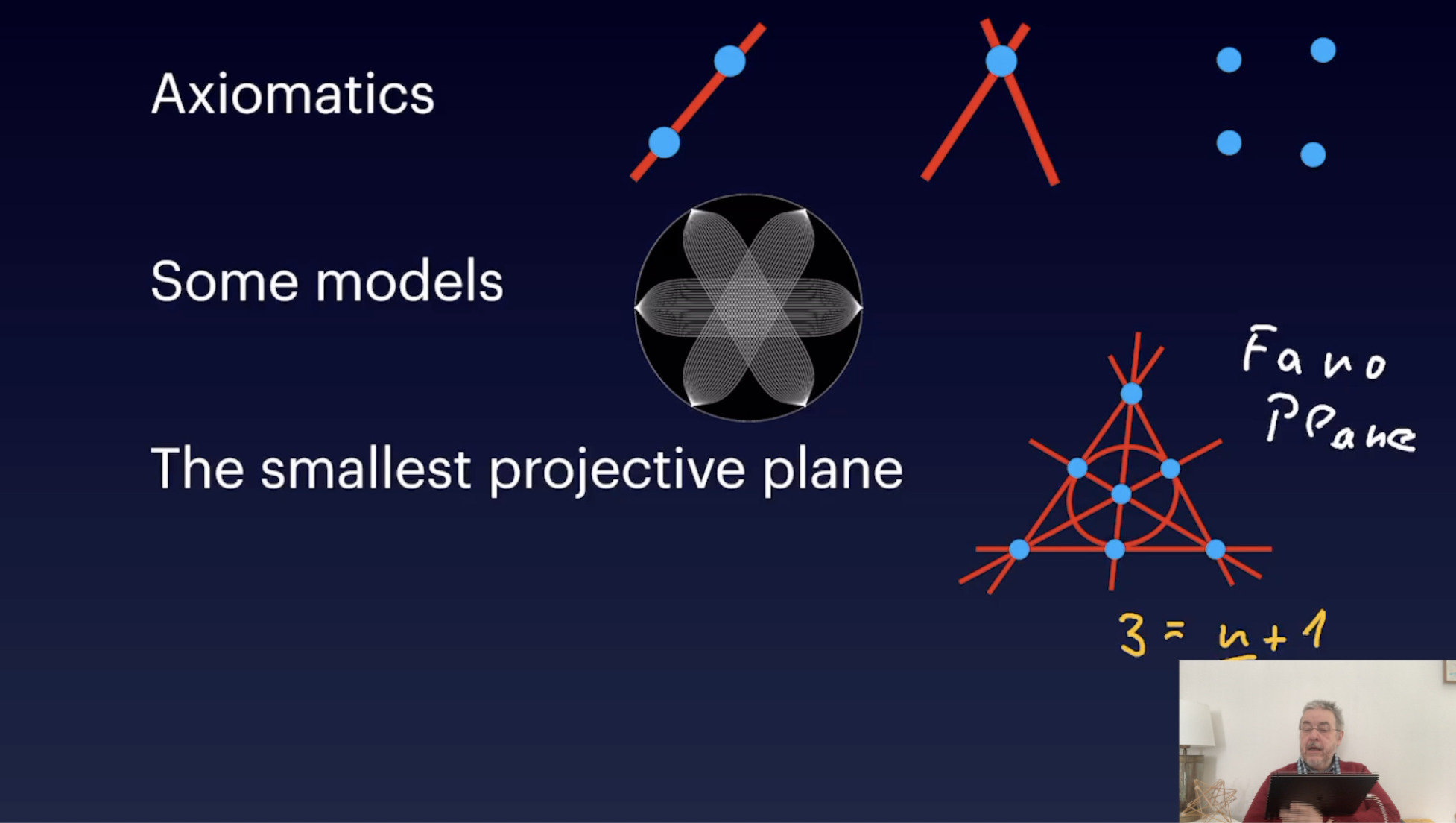
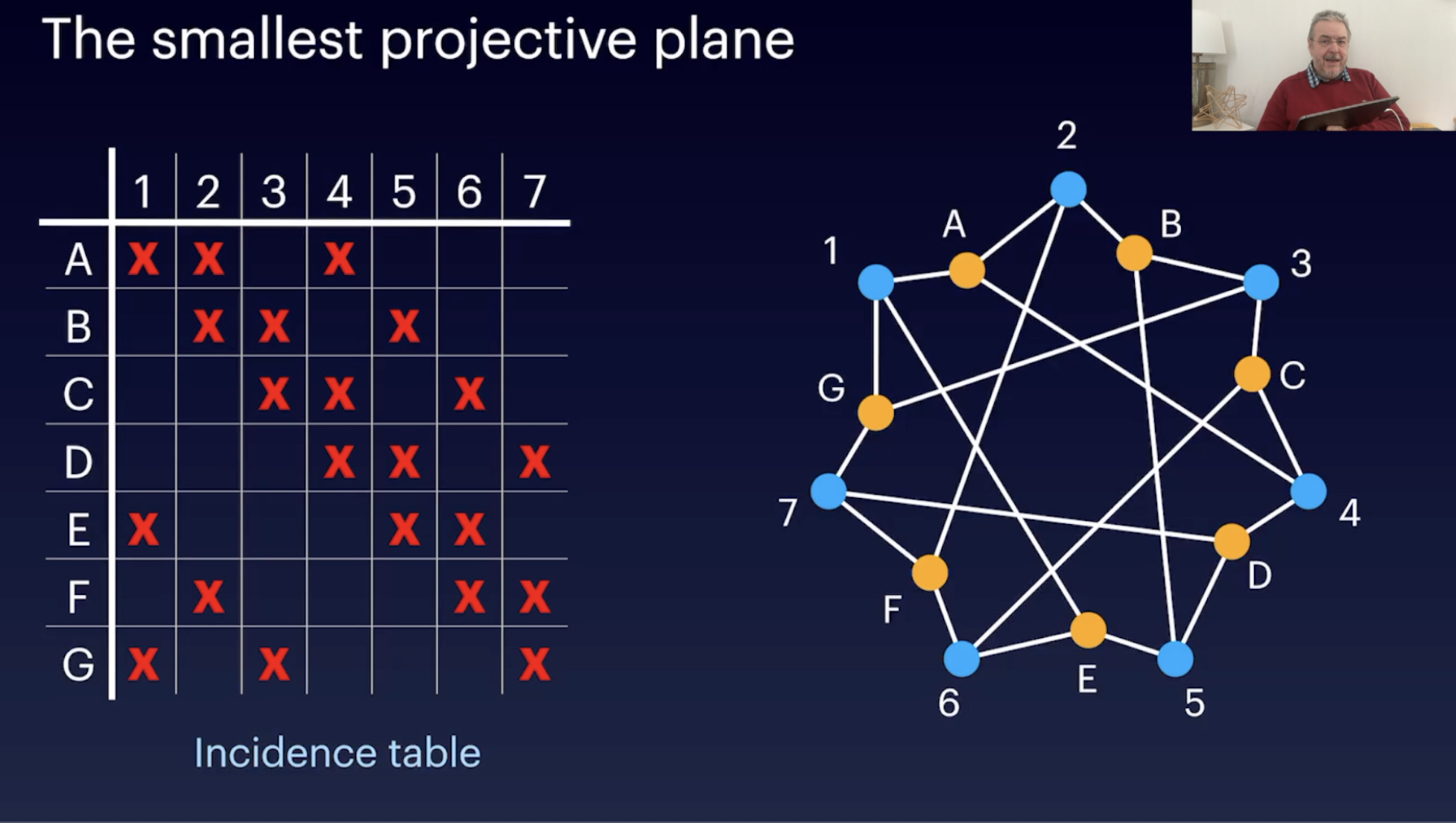
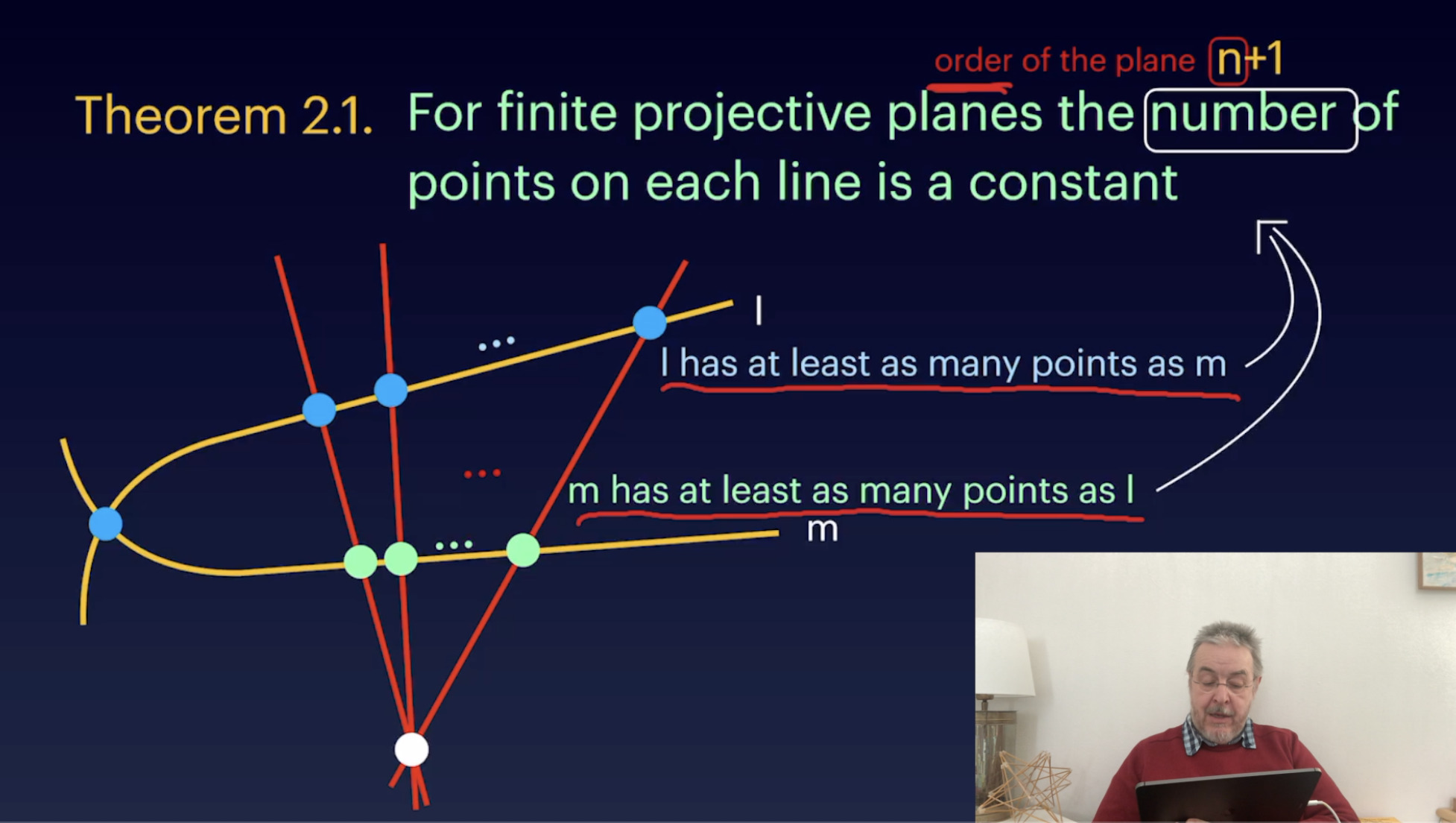
Introduction and a bit of history (21:35)
Axiomatics 1: PG Axioms (14:49)
Axiomatics 2: Simple Models (26:27)
Axiomatics 3:First conclusions (19:16)
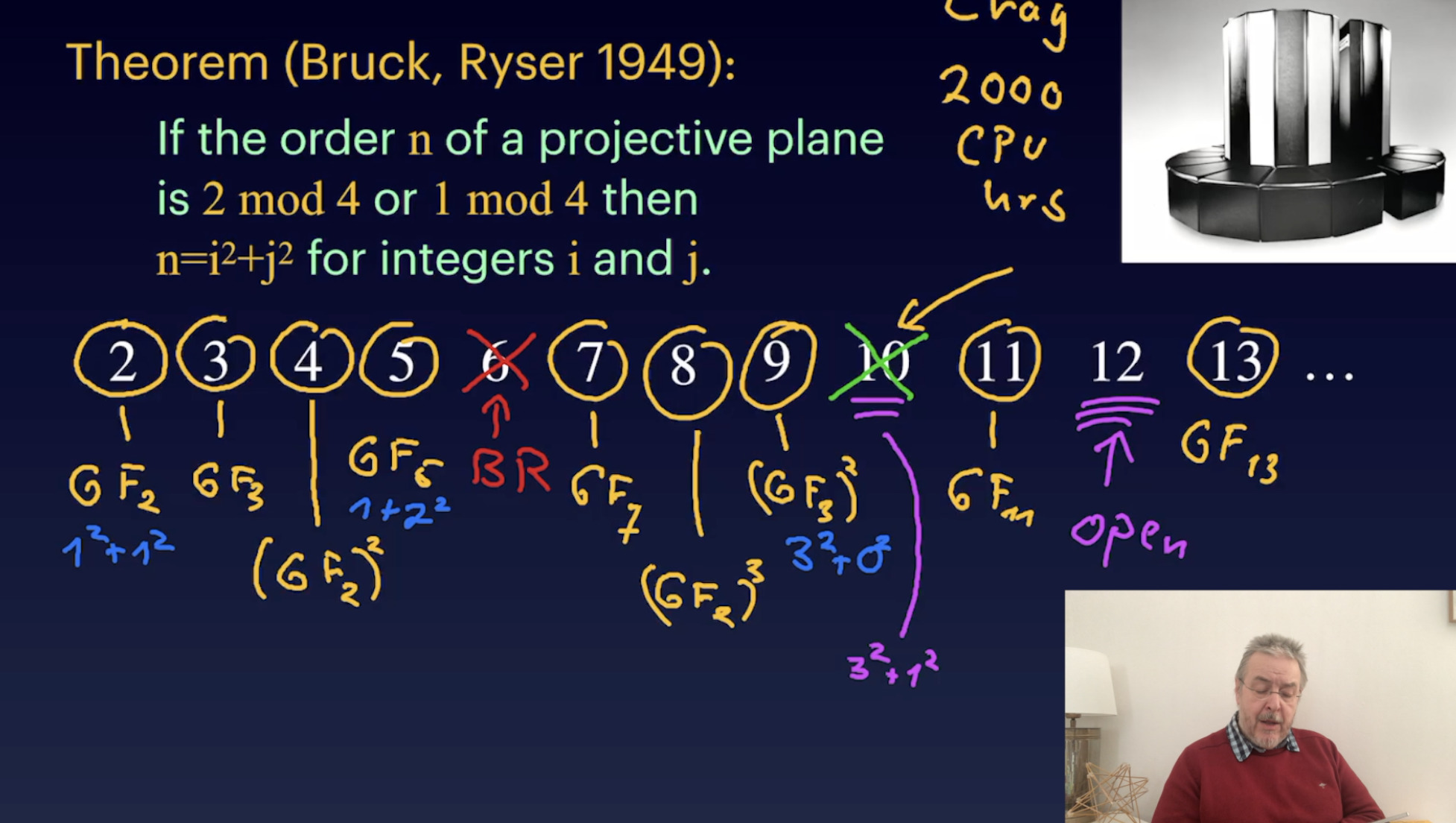

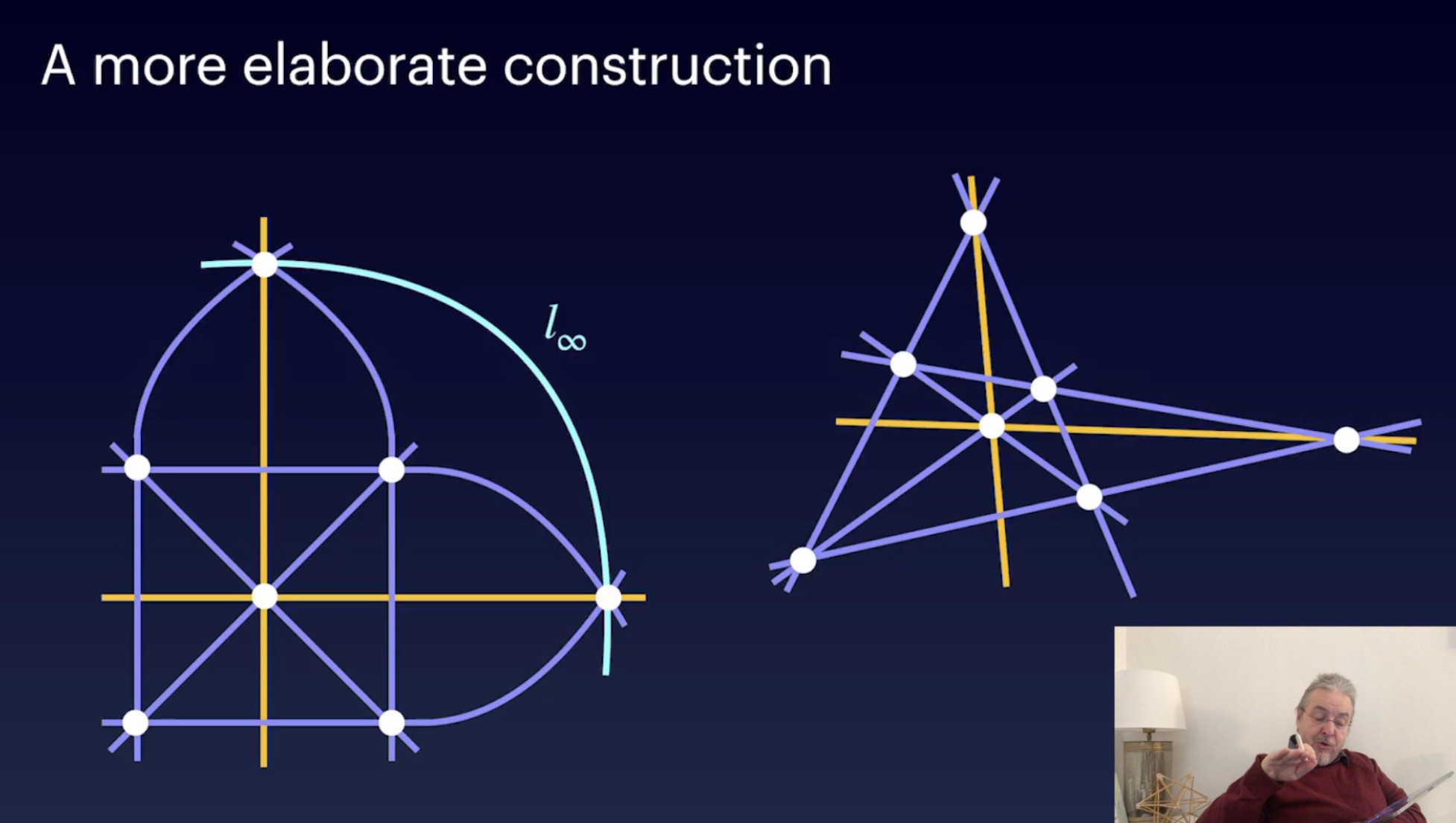
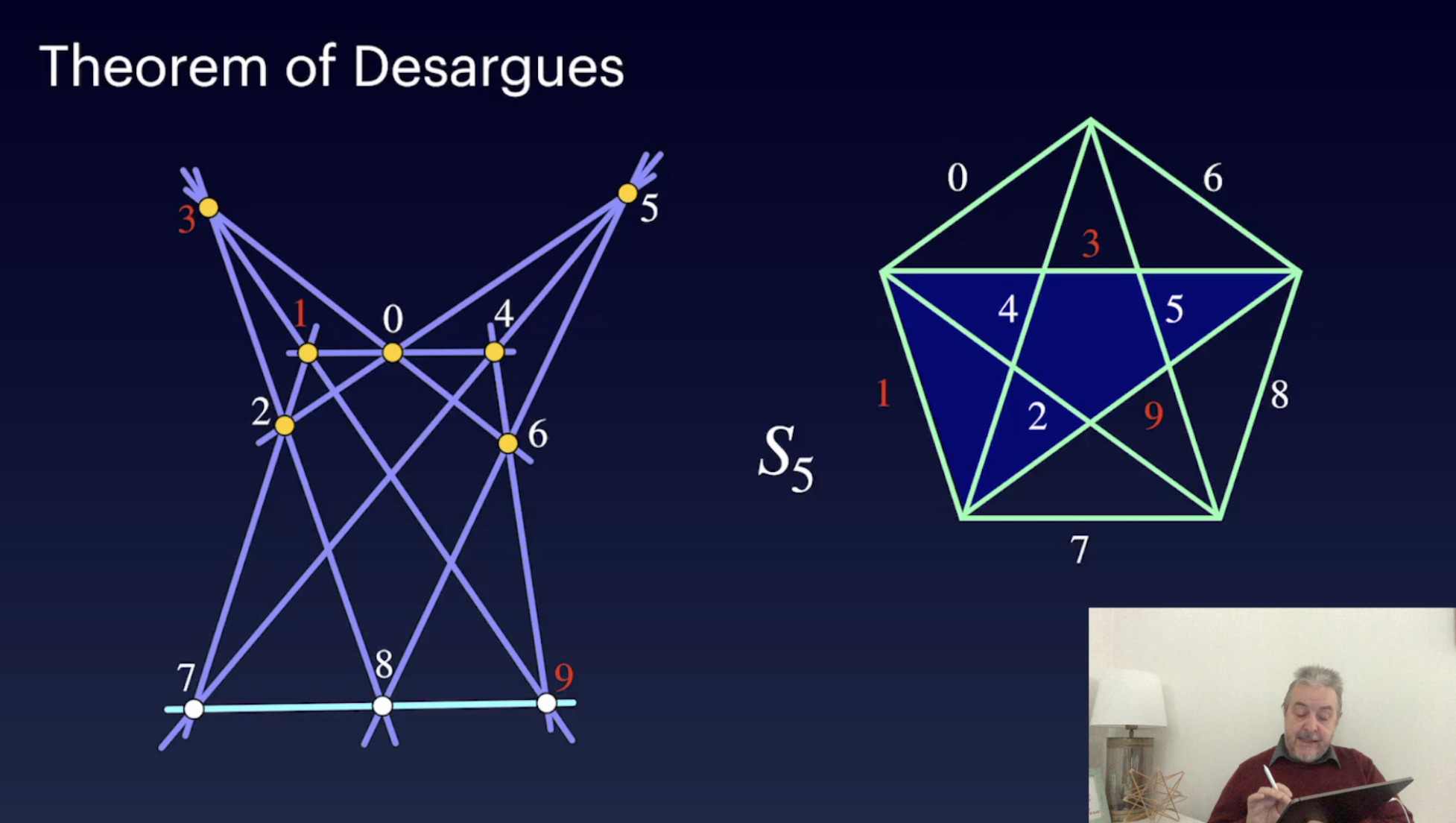
Homogeneous coordinates & finite projective planes (32:47)
Homogeneous coordinates in RP2 (20:34)
Join and Meet in RP2 (20:47)
Pappos/Desargues (32:36)

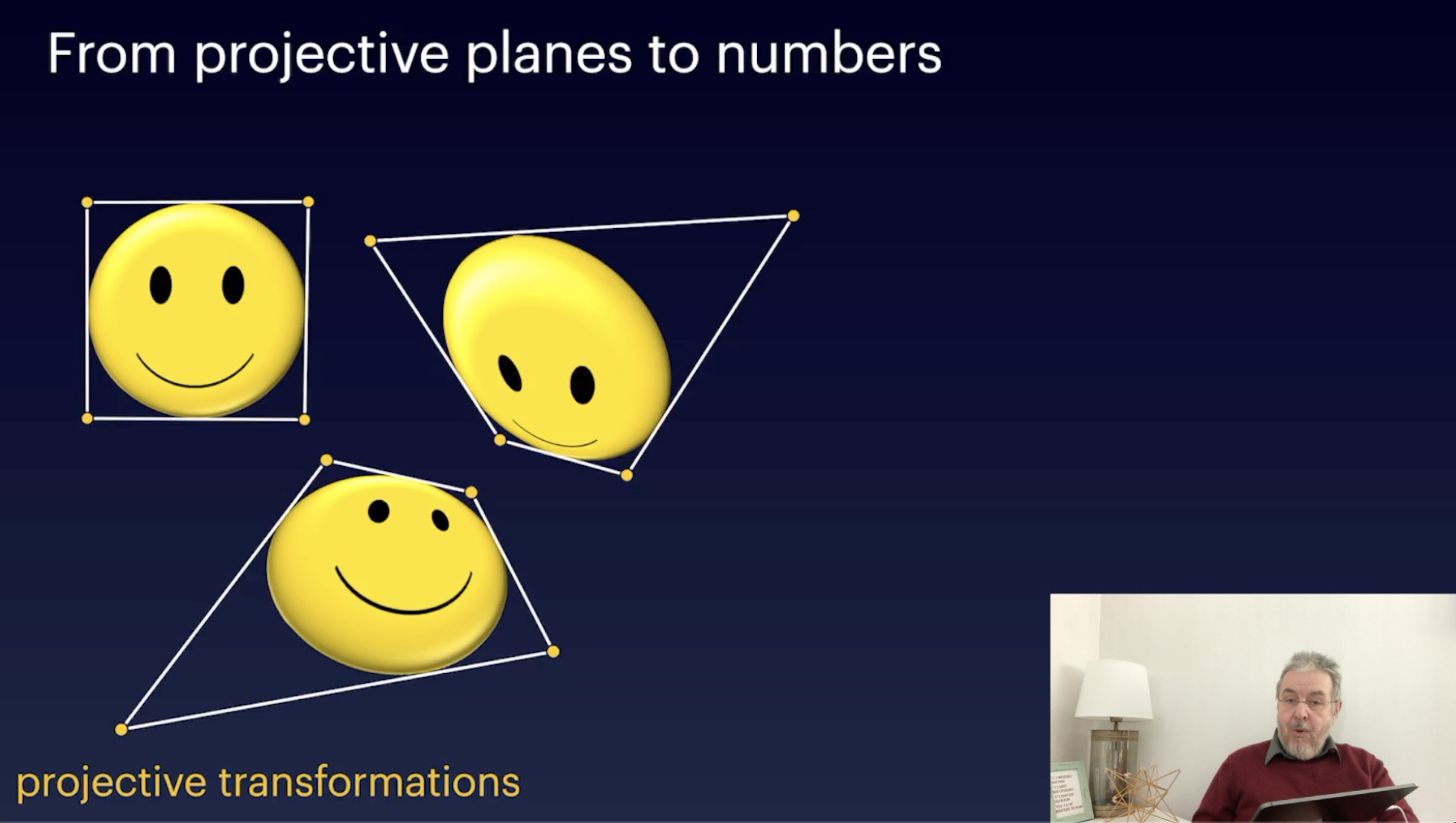
Transformations and Collineations (26:57)
Projektive invariants and Cross Ratios (19:52)
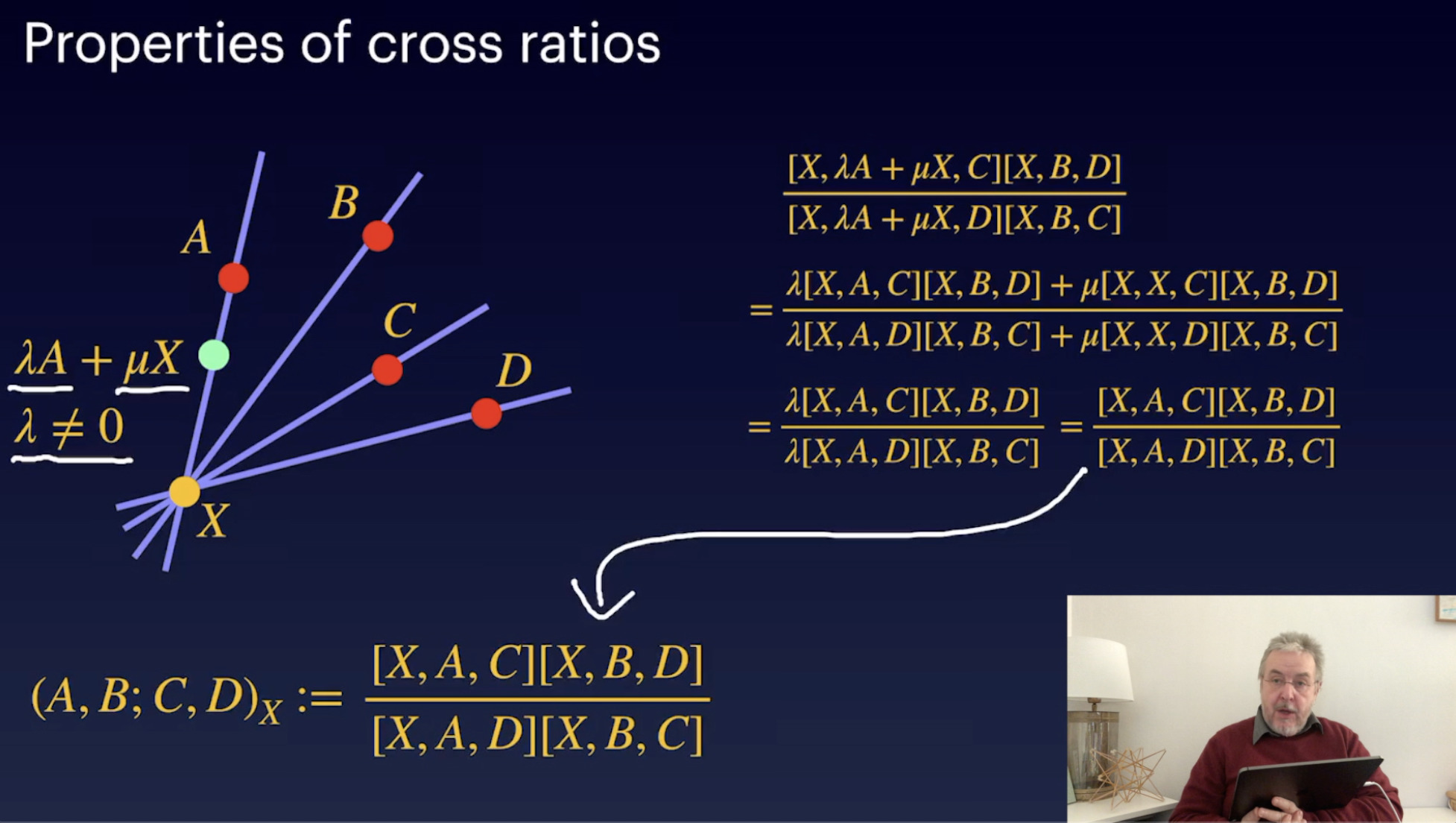
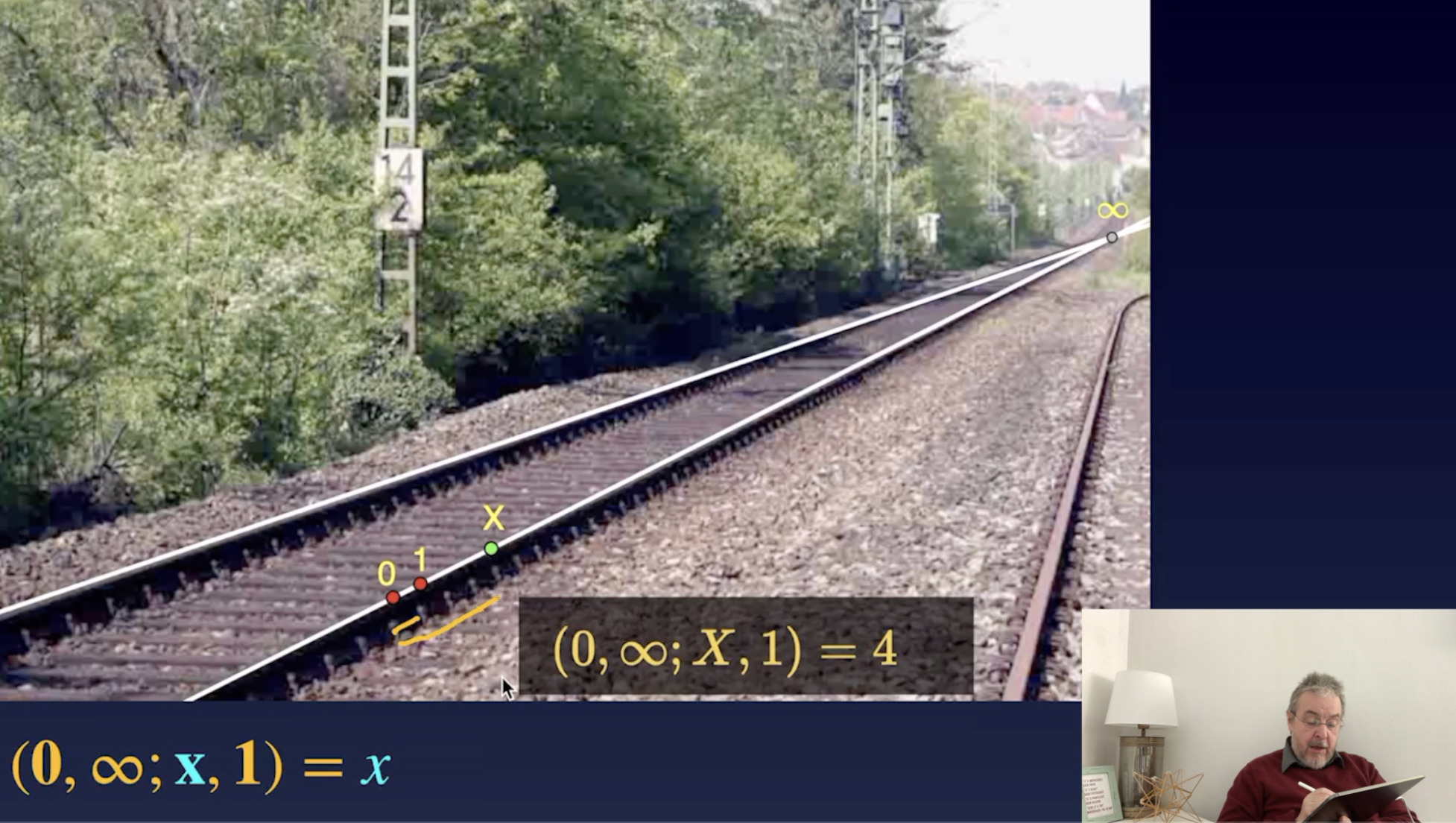
Properties of Cross Ratios (20:36)
The projective line (9:13)
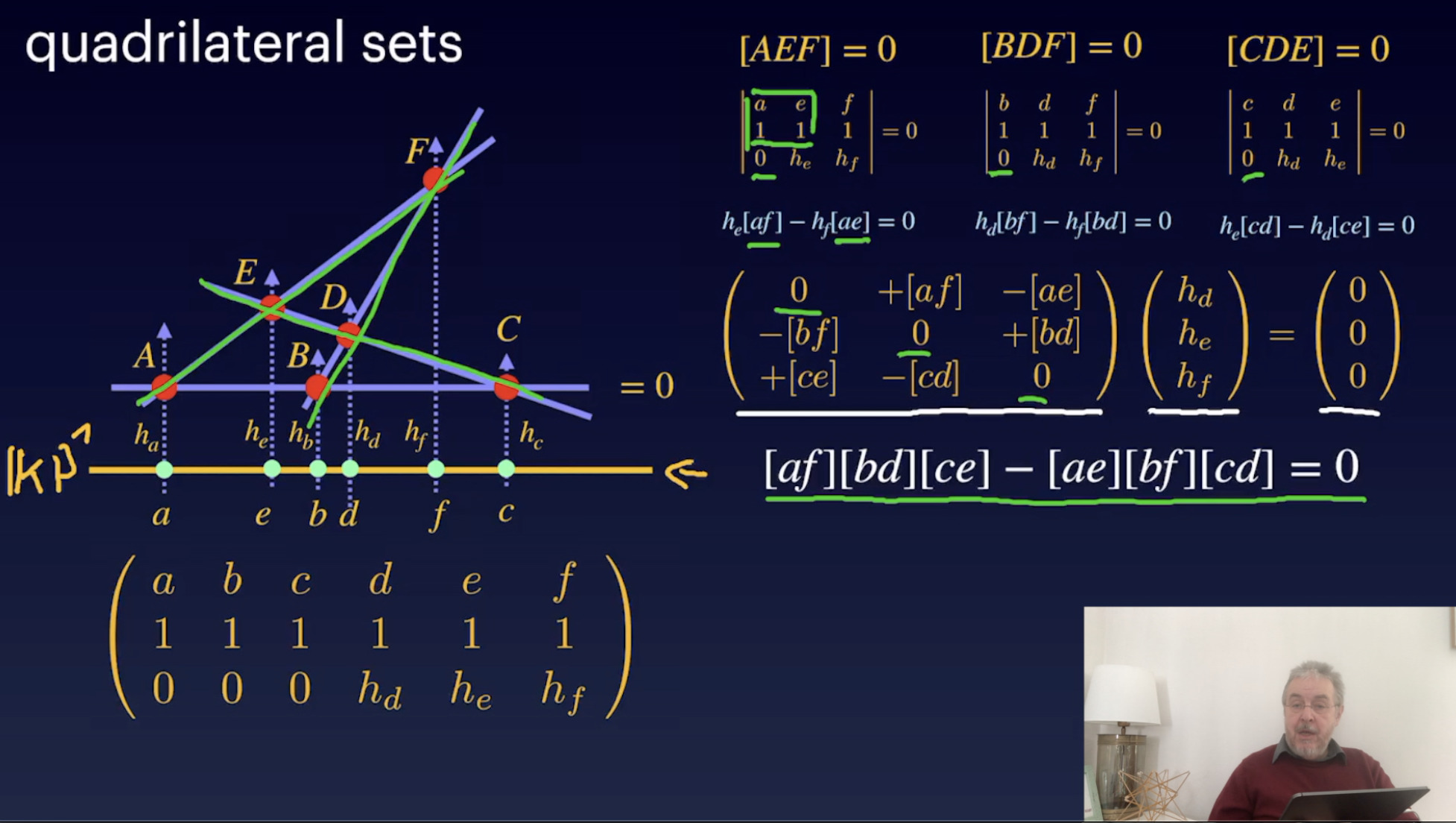
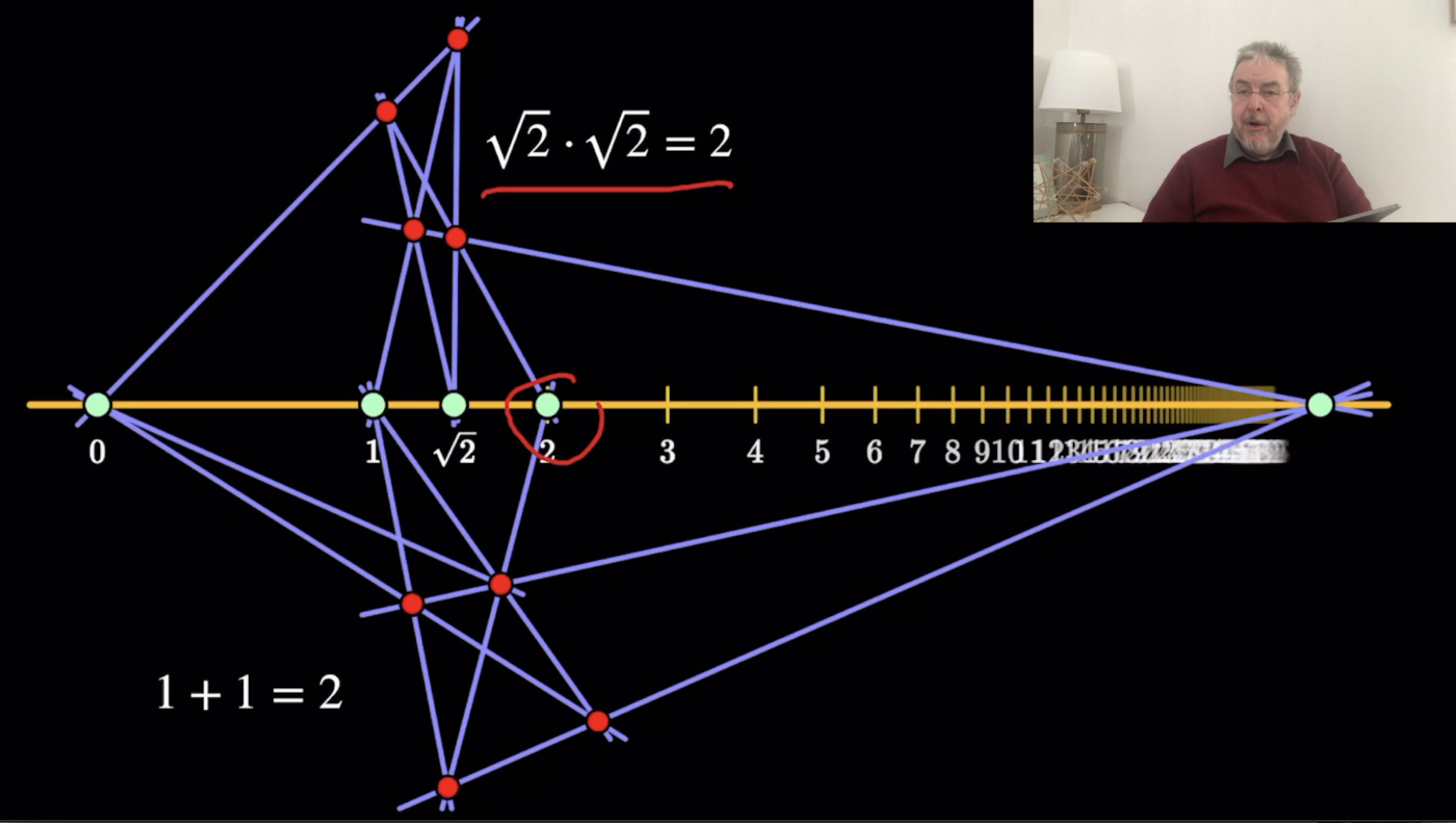
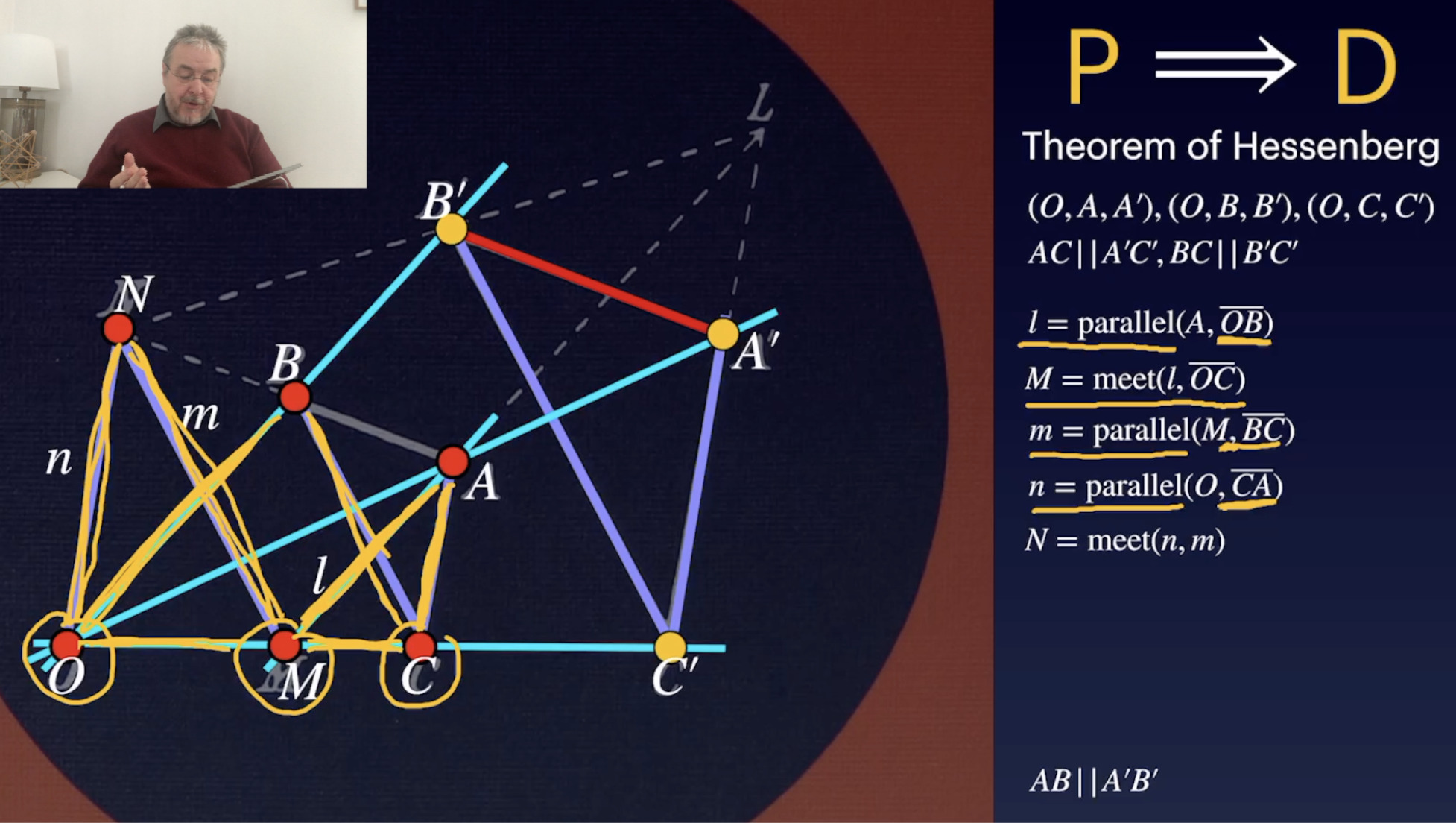
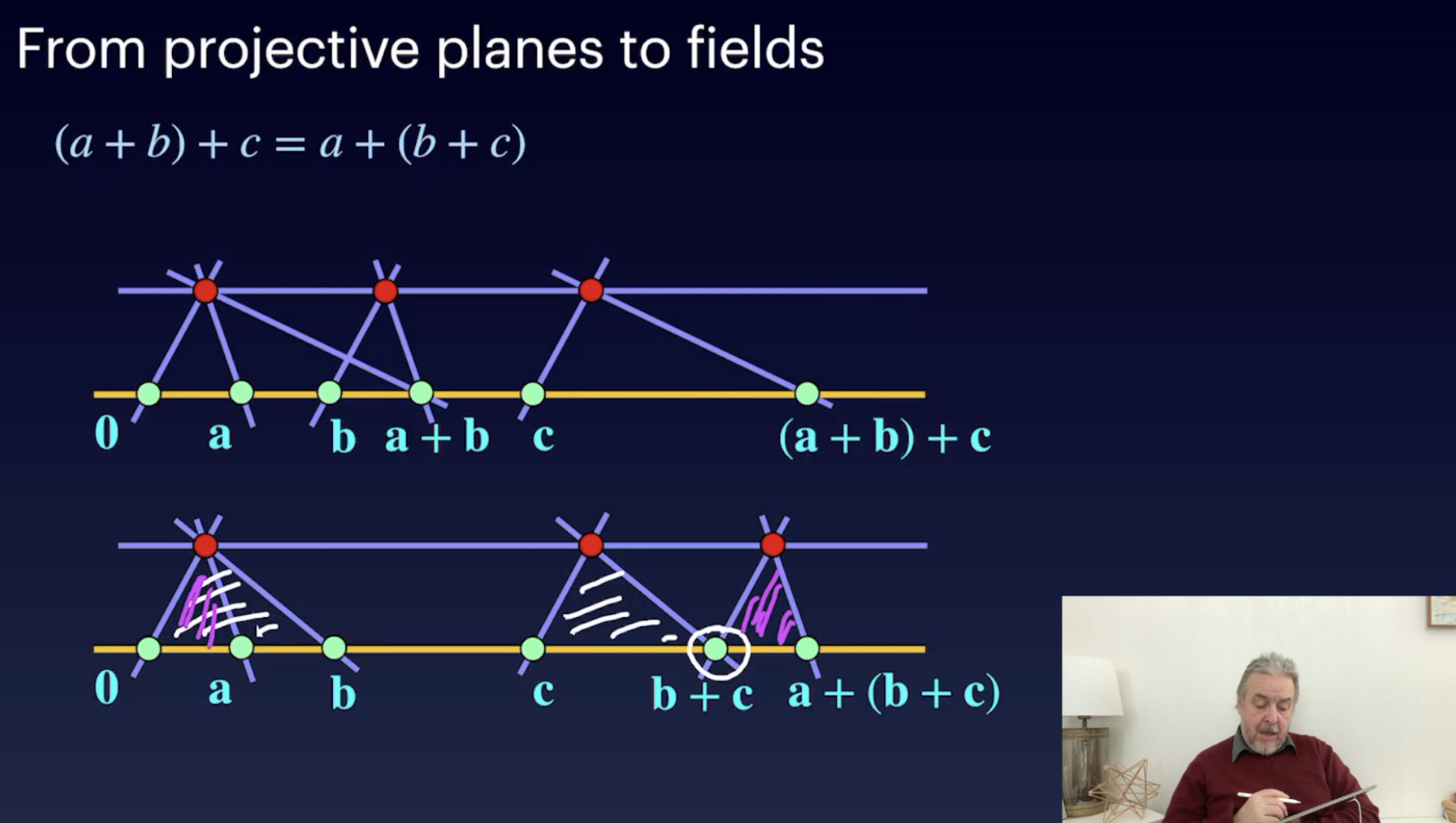
Quadsets und Harmonic Sets (30:14)
Von Staudt Contructions (38:45)
Five useful incidence theorems (27:38)
From PG to Fields (45:16)

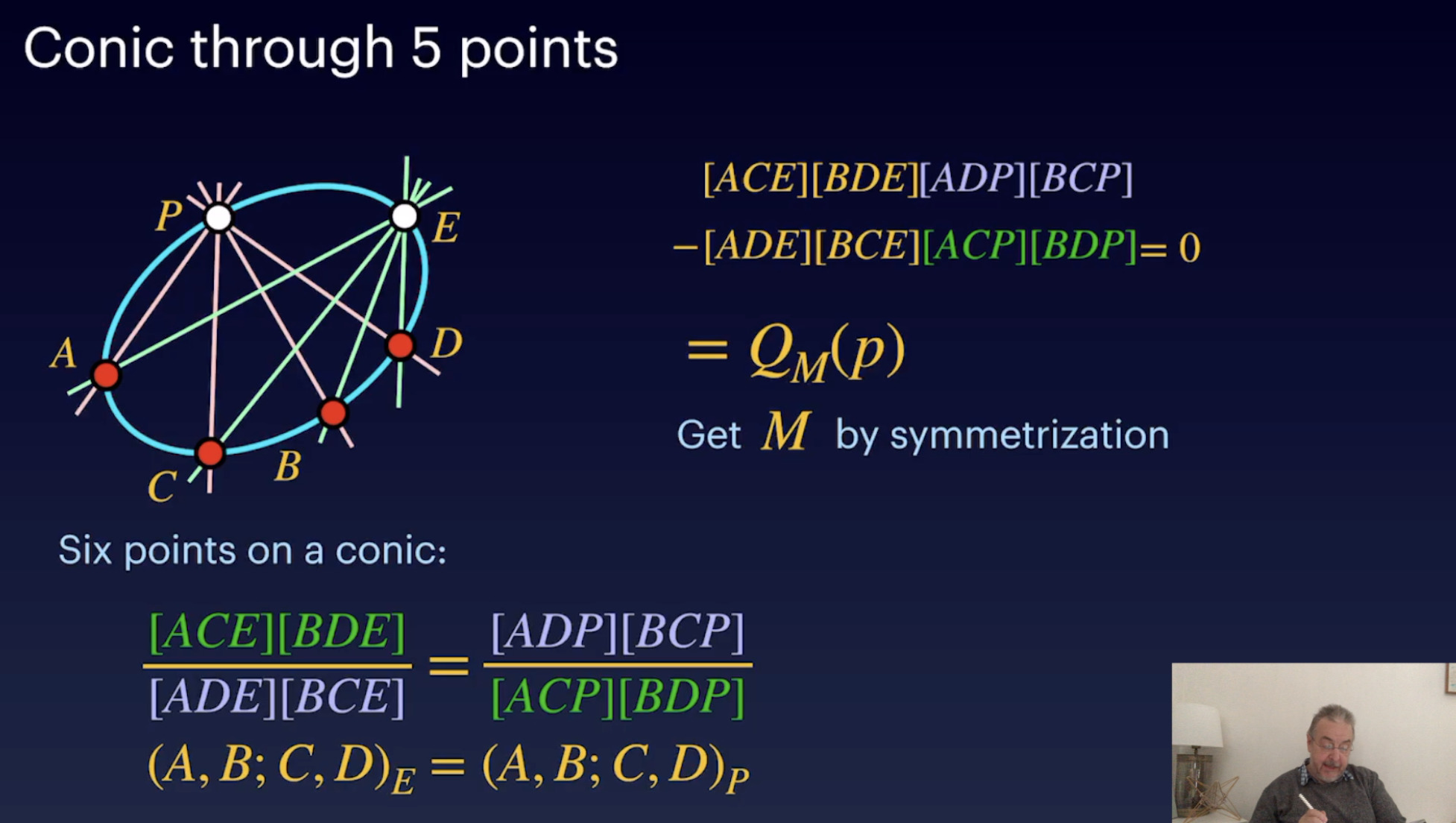


Conics (Difinition and Classification) (28:20)
Conic by 5 (11:33)
Polars and Duals (34:57)
Primitive Operations (24:59)



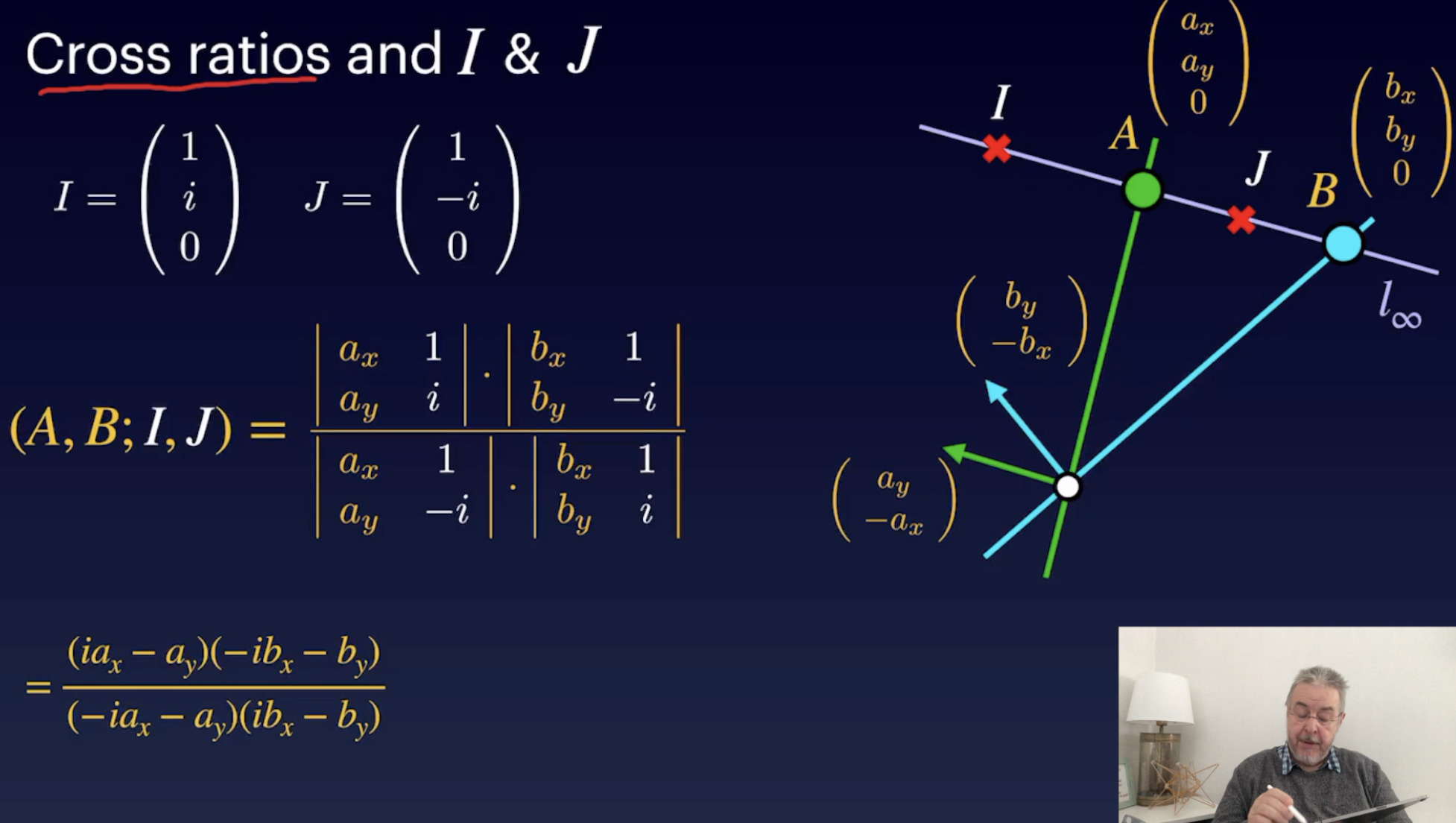
Scales on Conics (23:56)
Quadsets on Conics (24:38)
CP1 Essentials (43:22)
CP1 vs. RP2 (32:30)

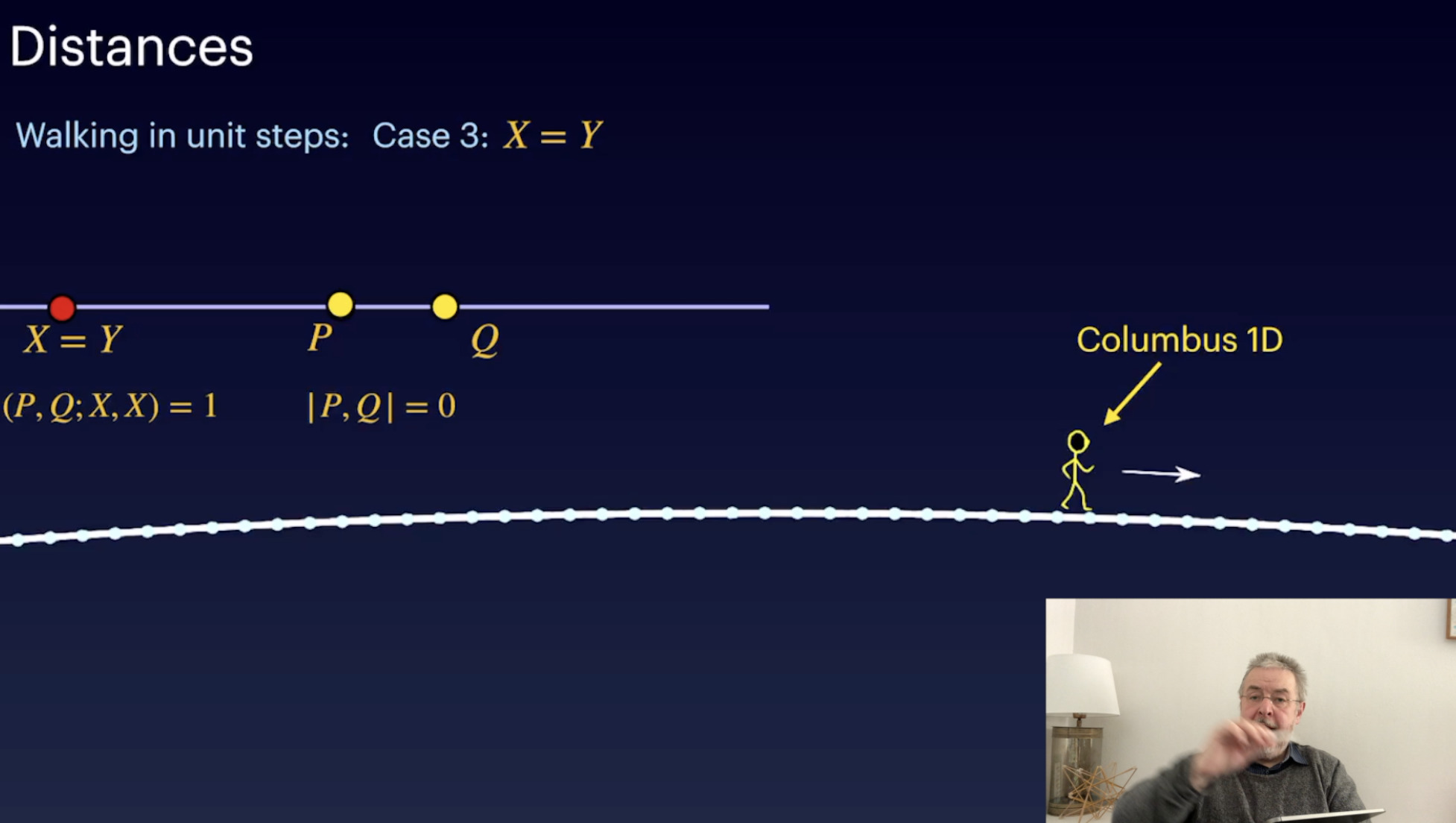
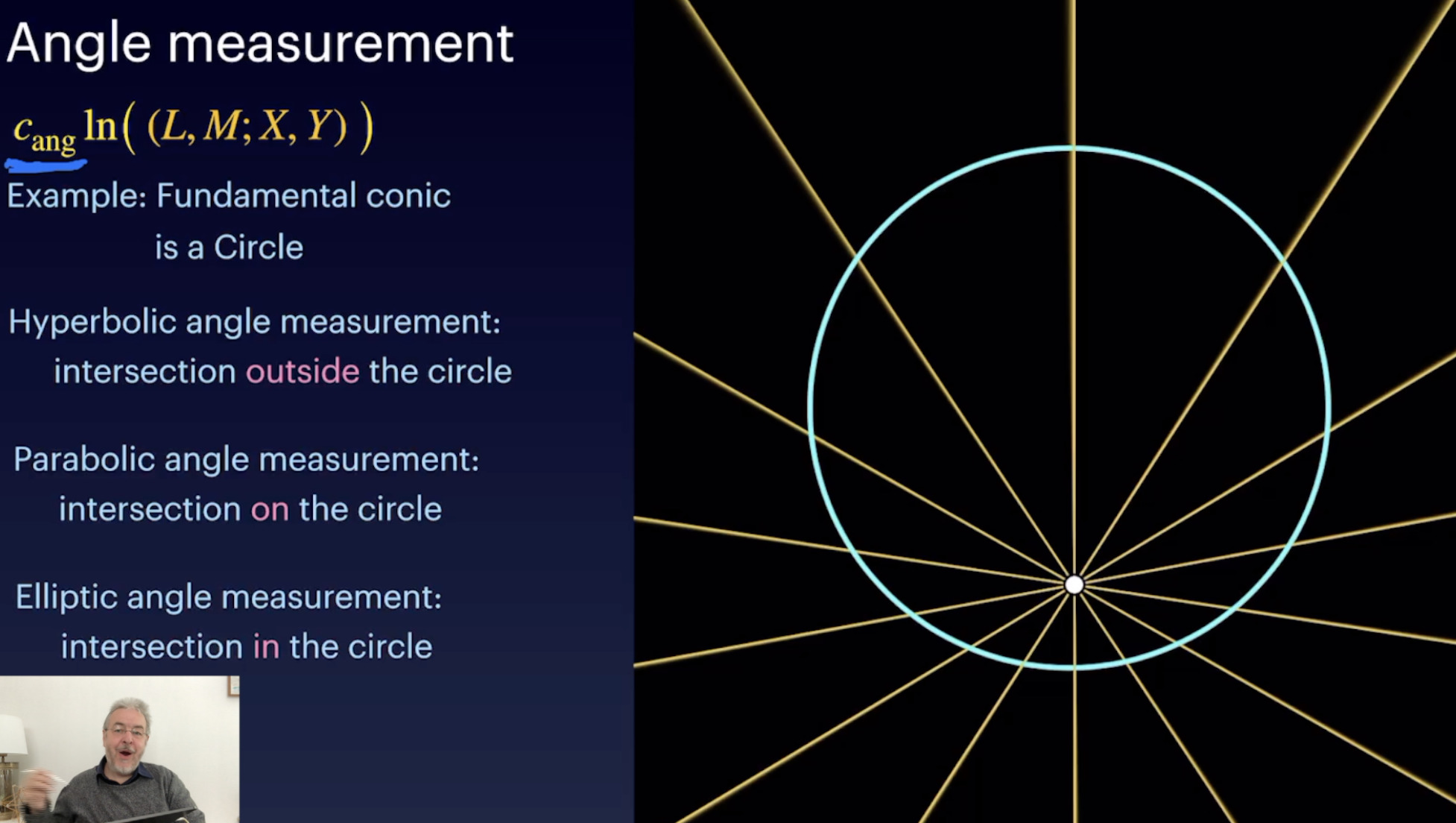
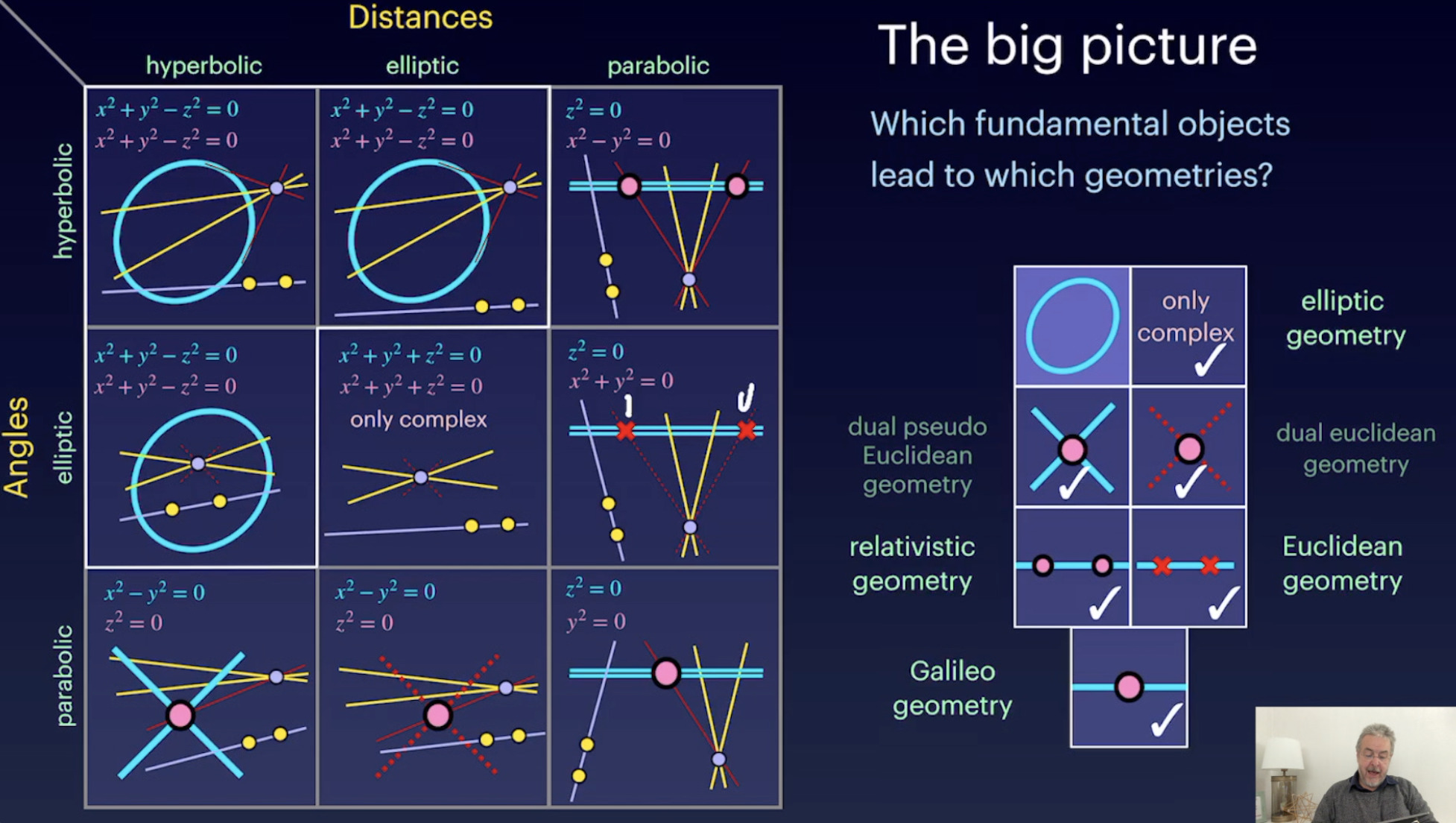
Cayley Klein Geometry Introduction (21:21)
Three Types of Measurements (29:36)
Angle Measurement (18:46)
Nine Types of Geometry (50:55)
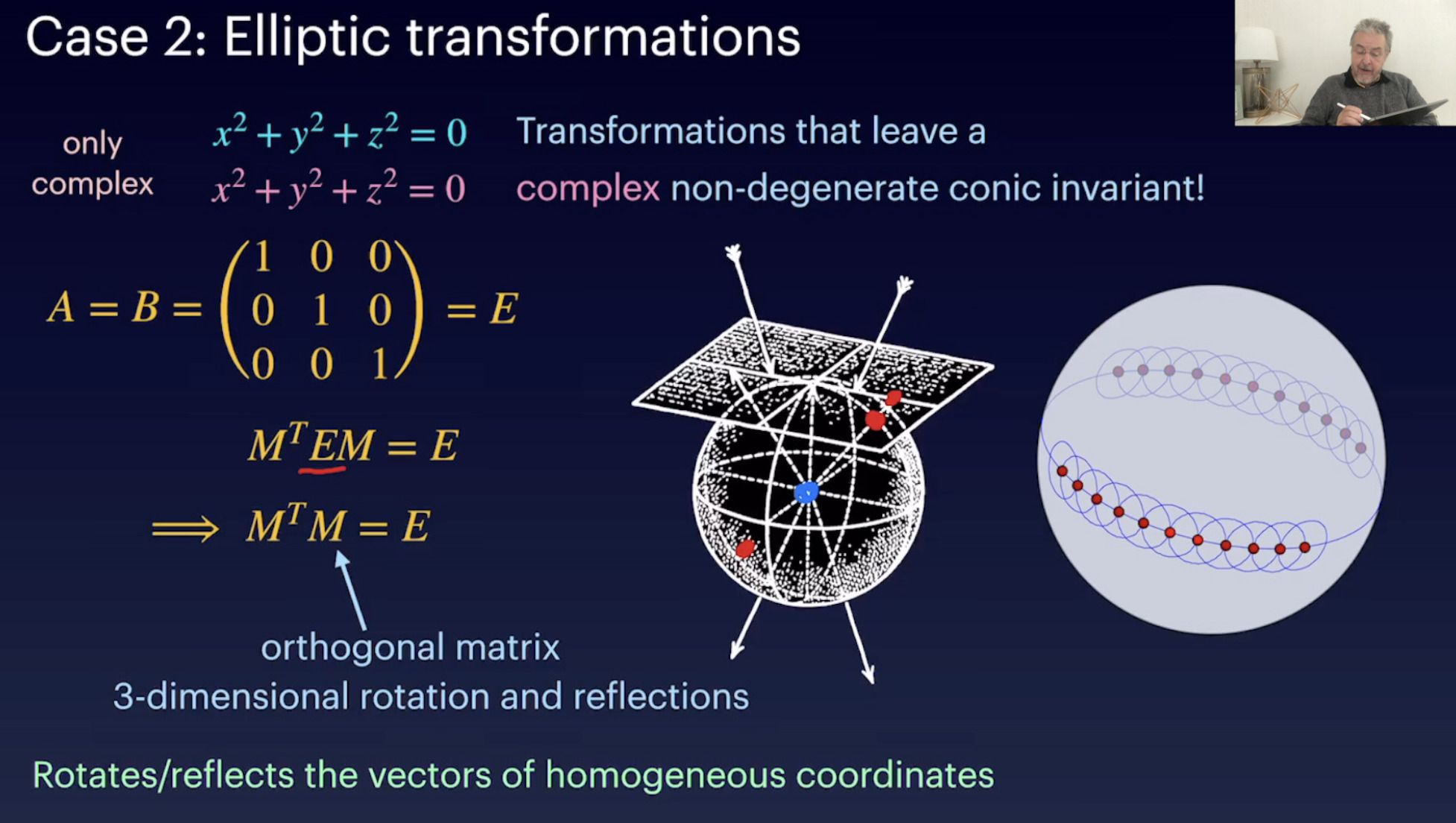

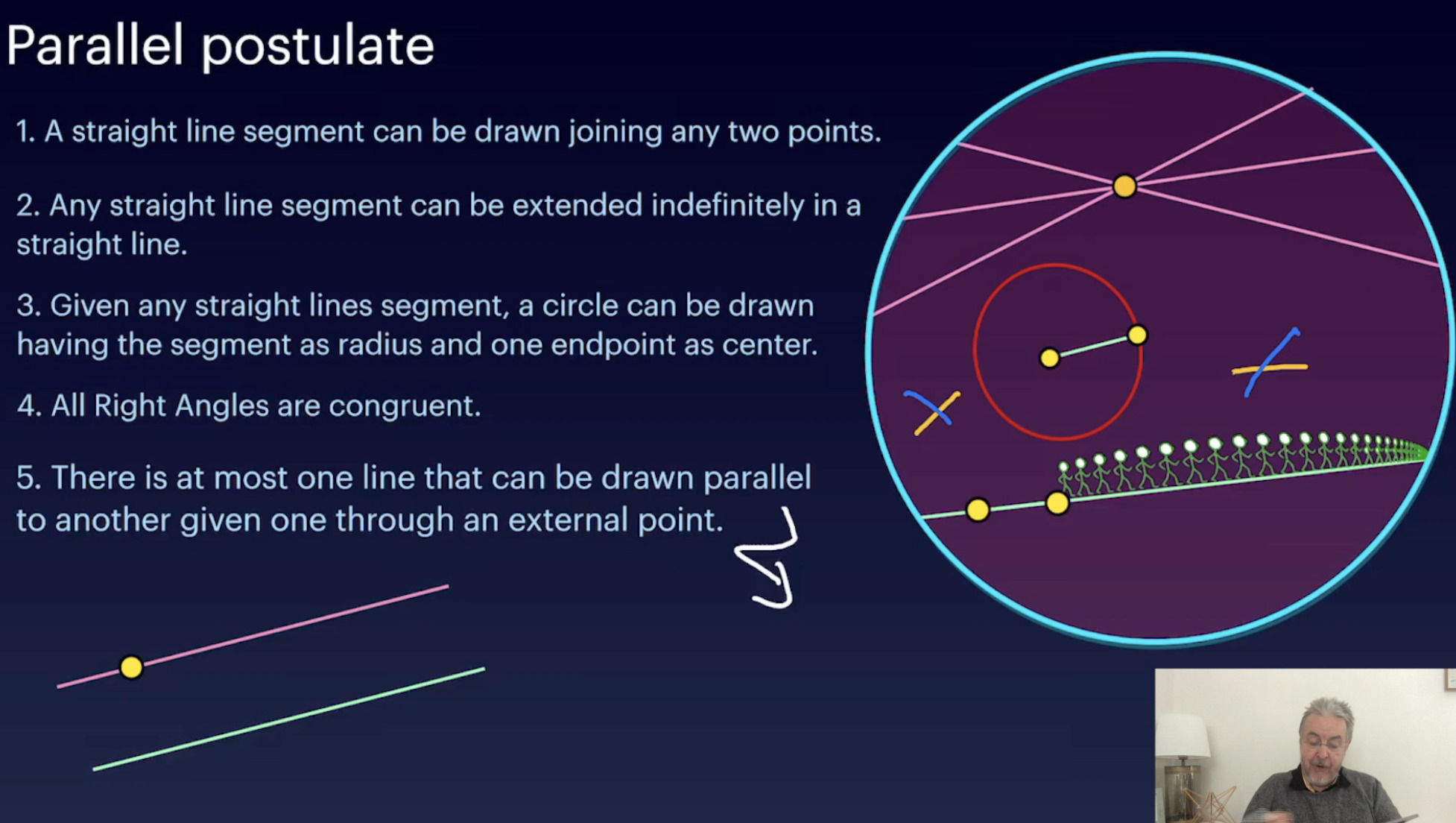

Cayley Klein Transformations (31:42)
Cayley Klein Elementary Geometry (45:16)
Hyperbolic Geometry, History (37:45)
The Poincaré Model (32:50)
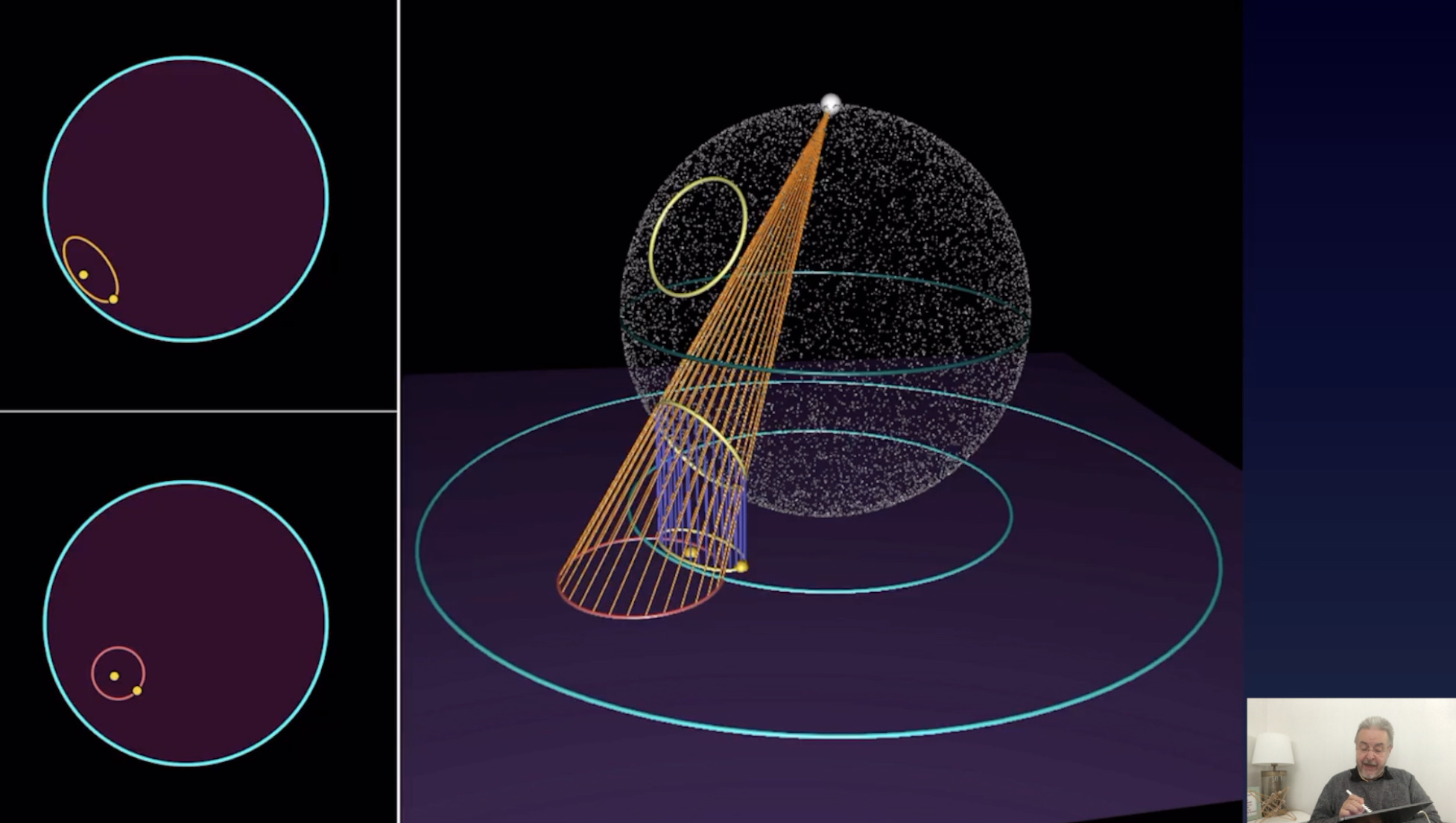
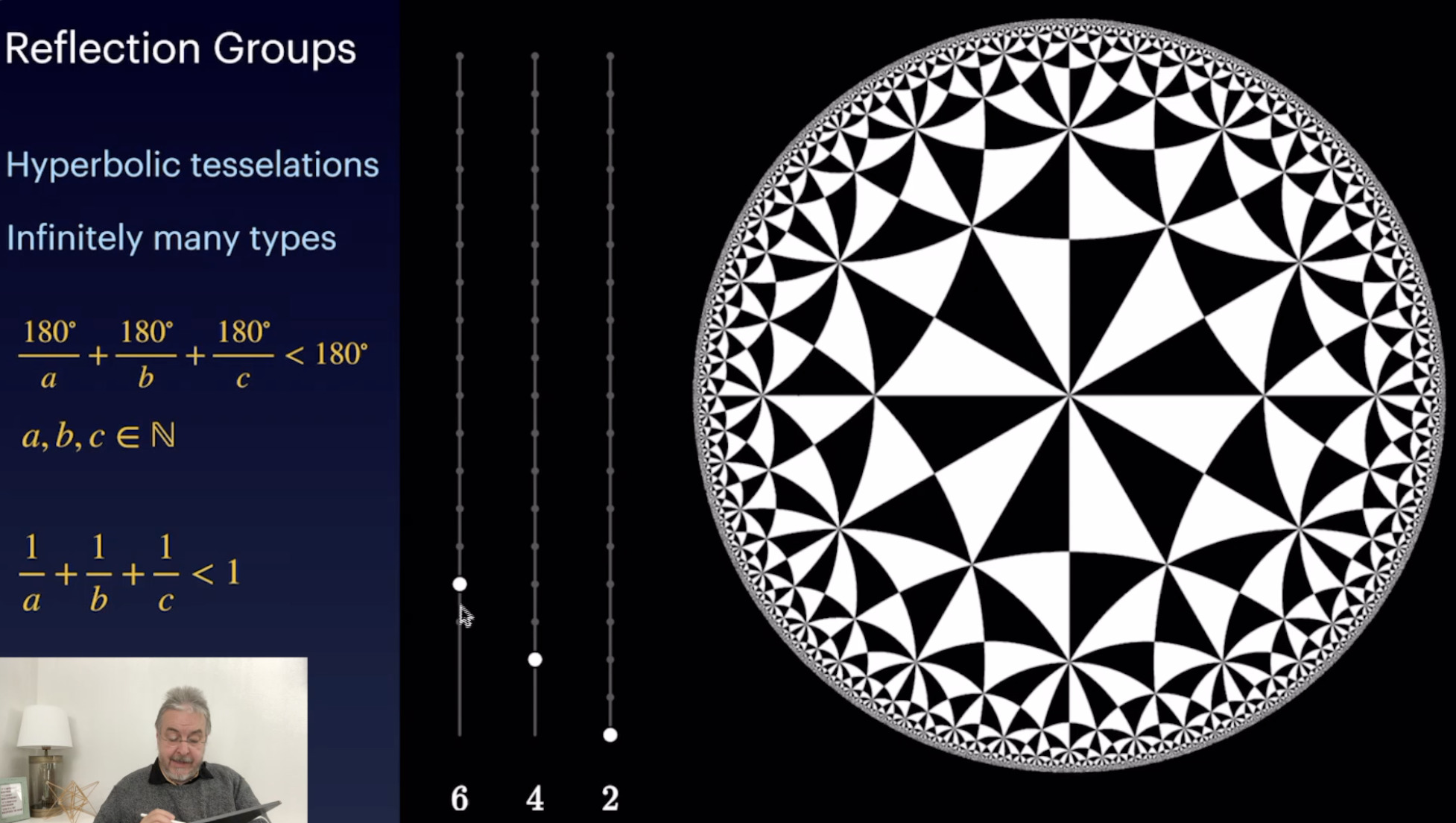
3D Interpretation of the Poincaré Model (30:13)
Triangles and Tessellations (52:52)
Projective Geometry 2

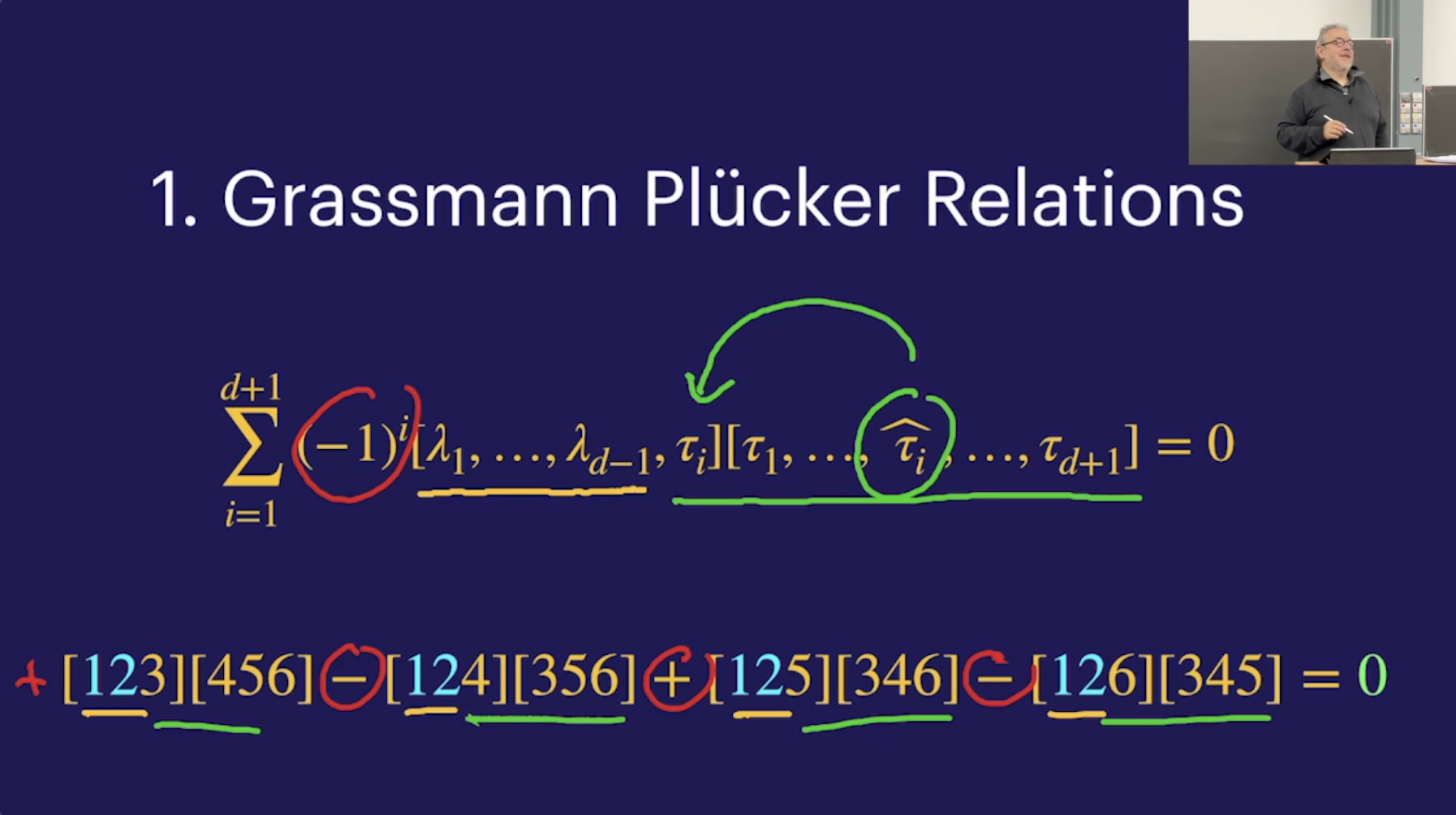

Determinants and invariants (1:00:16) [in class]
Grassmann Plücker relations (1:27:44) [in class]
Projectively invariant properties (1:37:14) [in class]
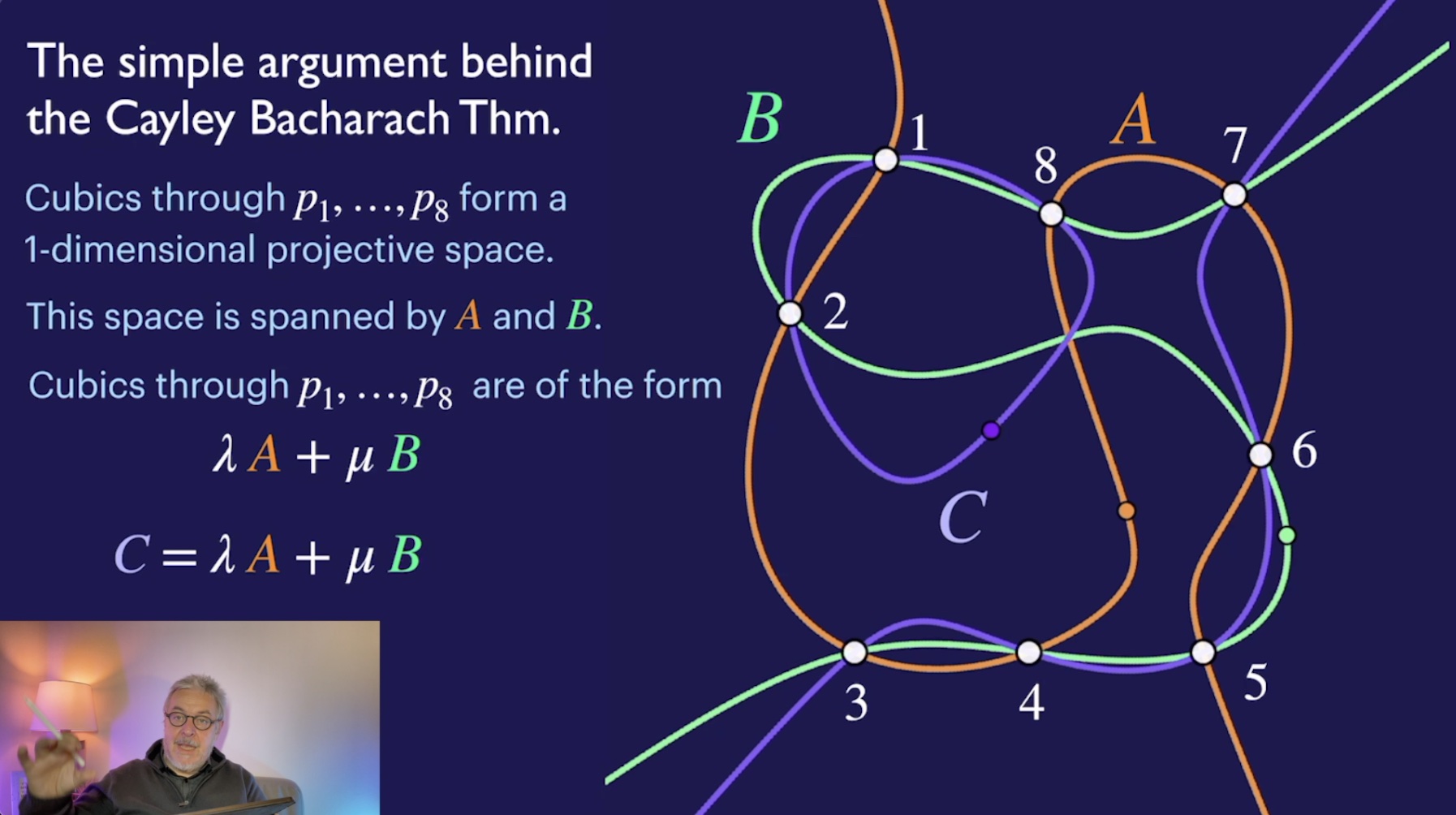
Bonus: The Cayley Bacharach Theorem (1:28:08)
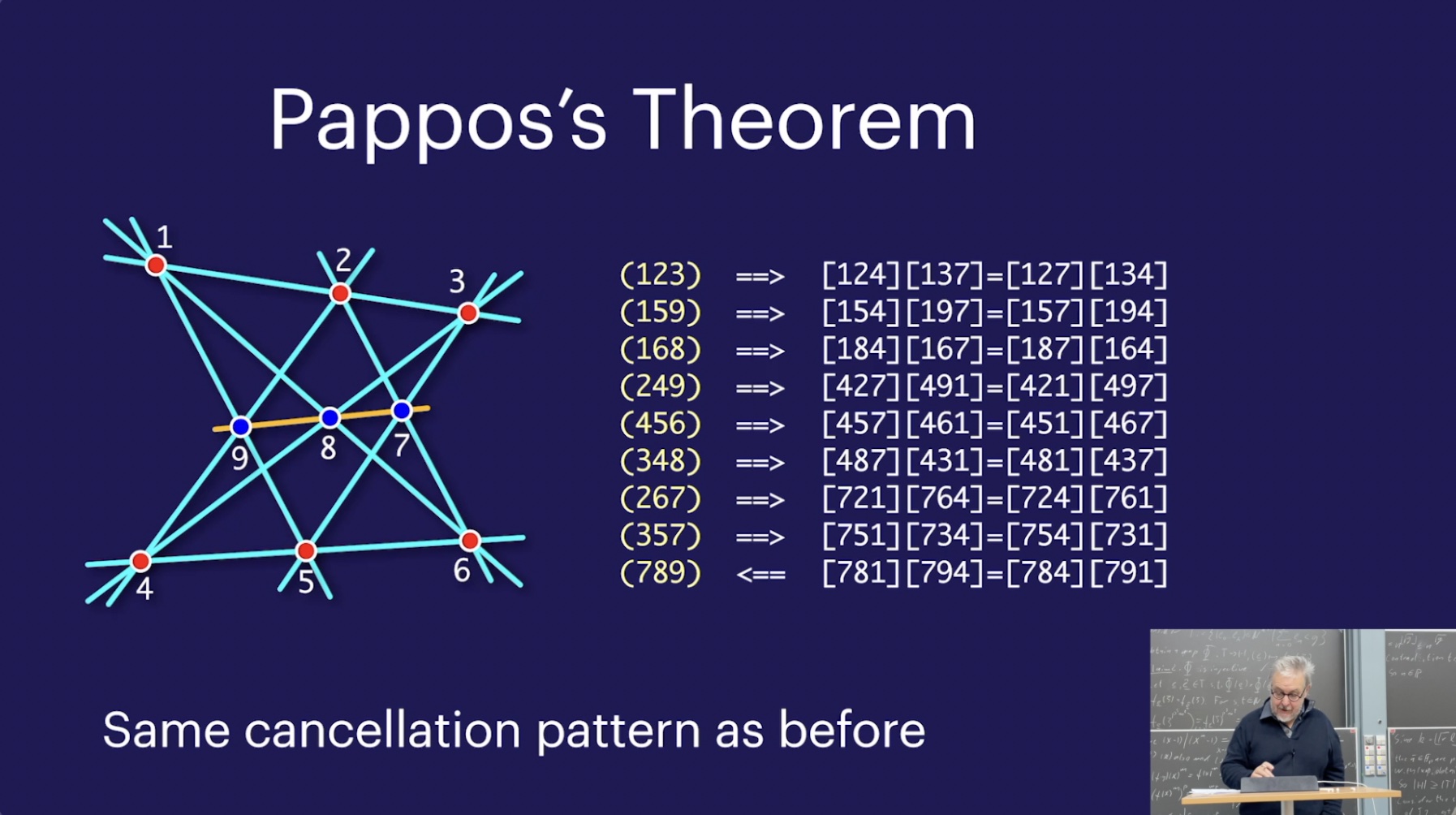

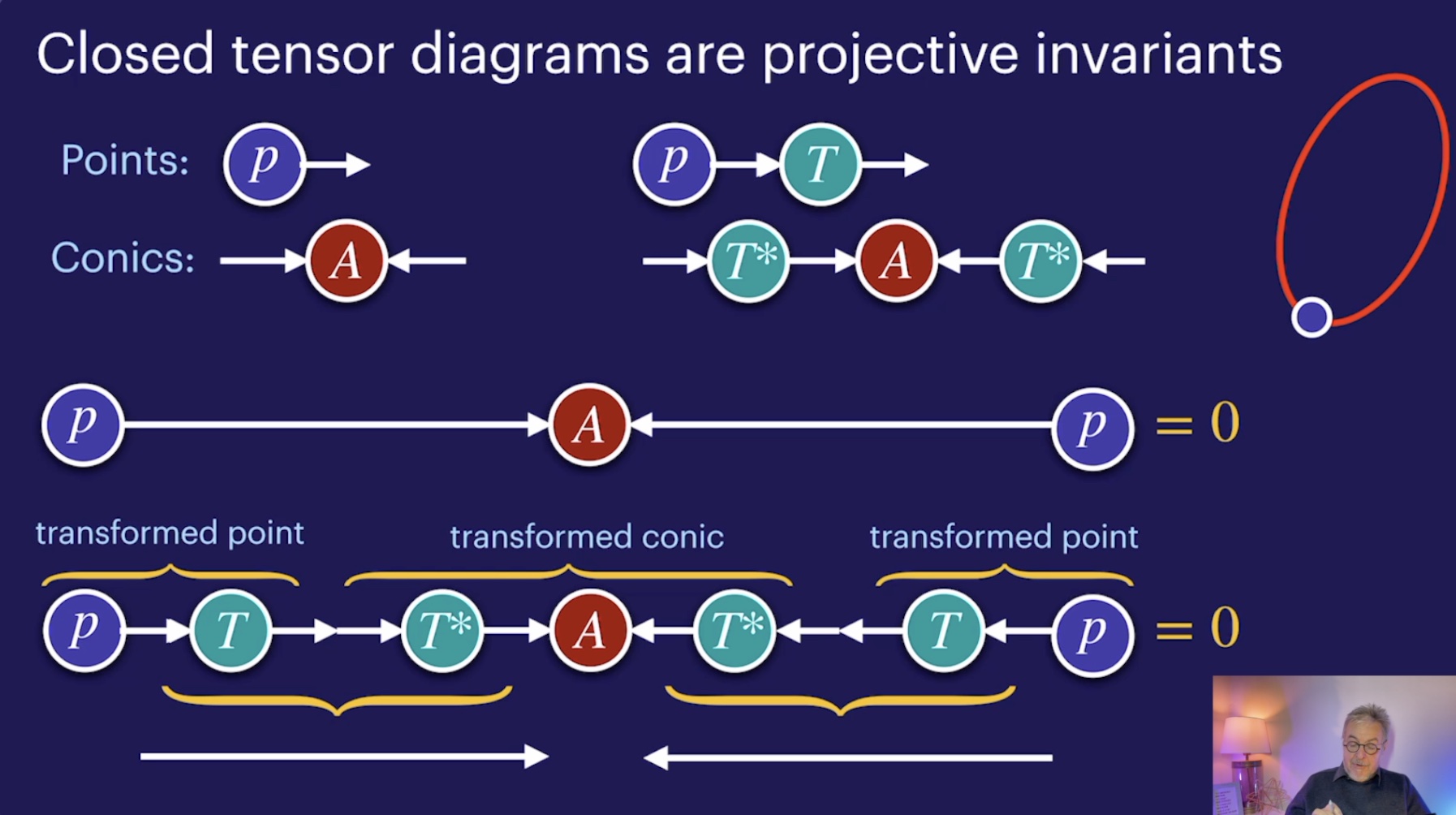
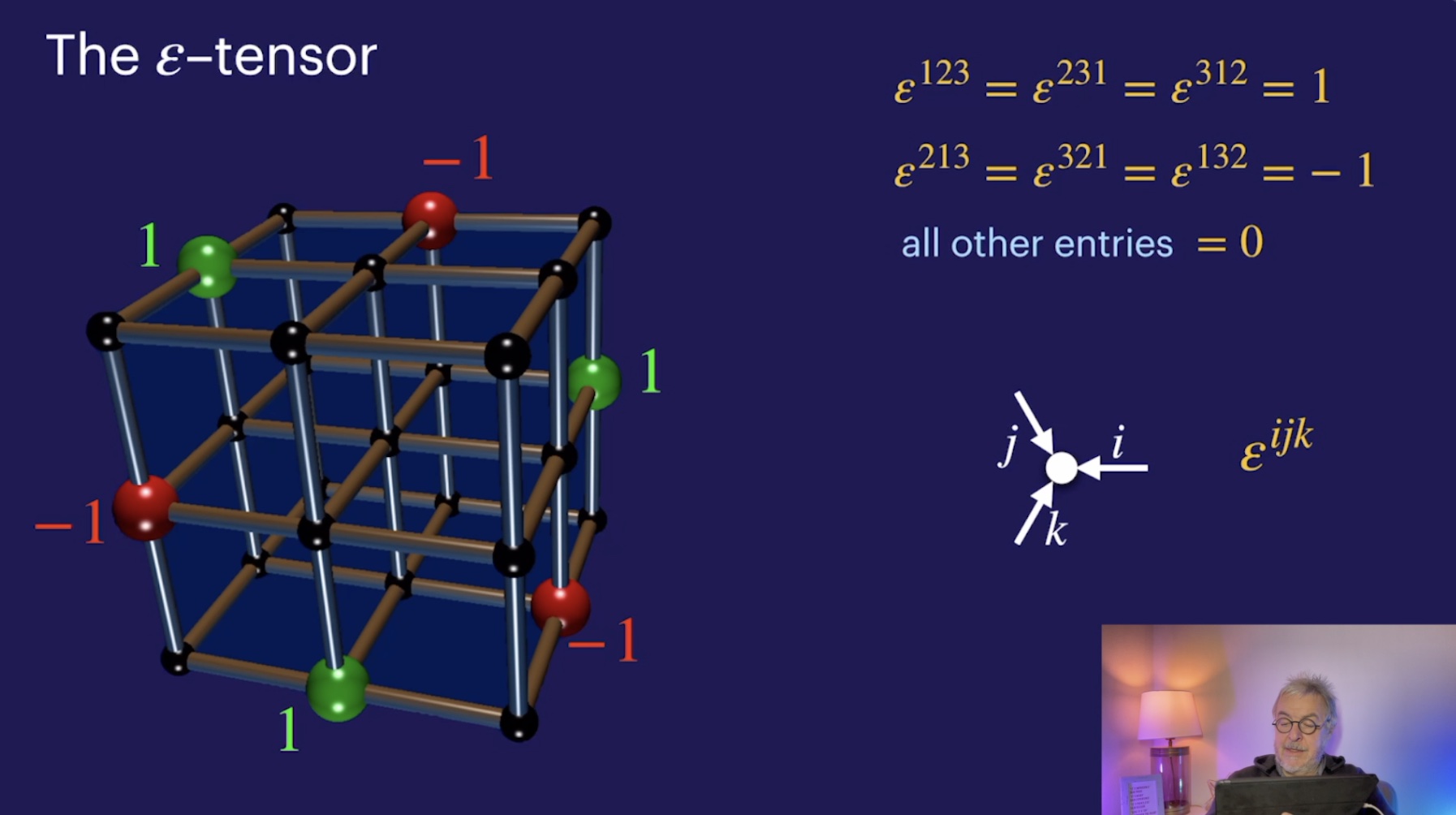
Interplay of points and invariants (1:27:49) [in class]
Tensor diagrams (42:28)
Transformations (21:03)
The epsilon-tensor (36:00)

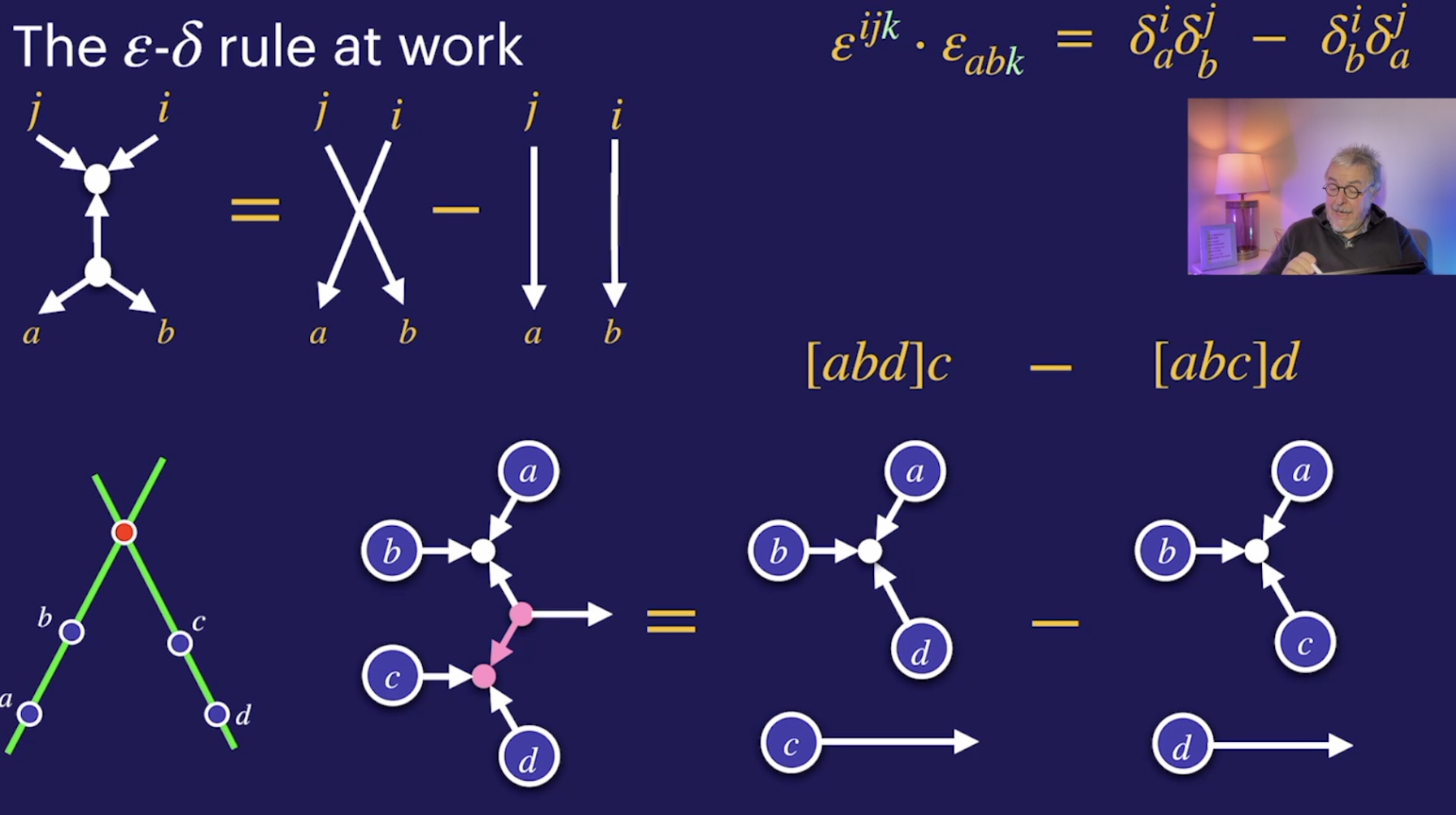

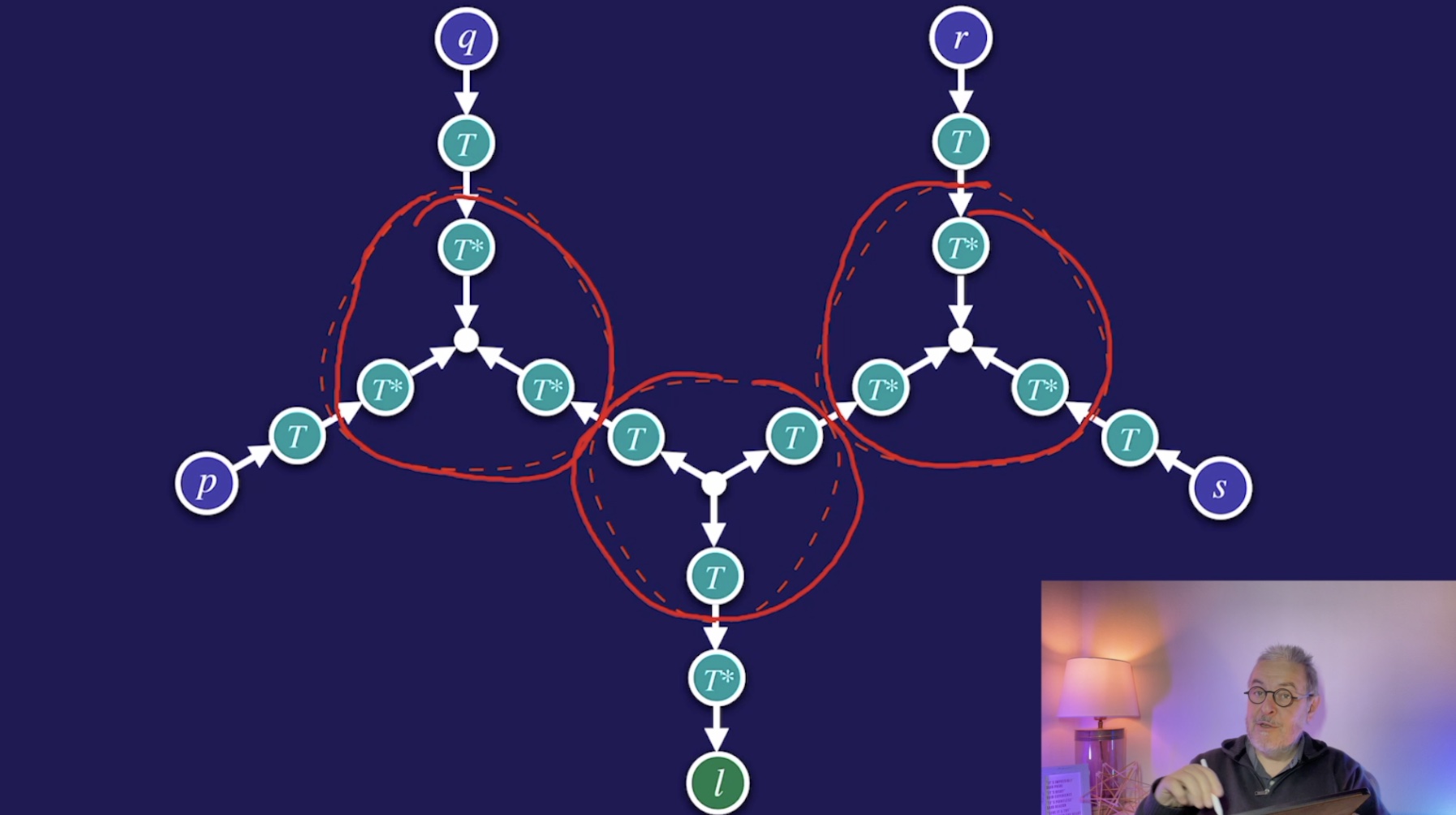
Rank 2 tensor diagrams (20:19)
The epsilon-delta-rule (20:05)
Proofs of the epsilon-delta-rule (30:32)
Transformations of epsilon-tensors (21:41)
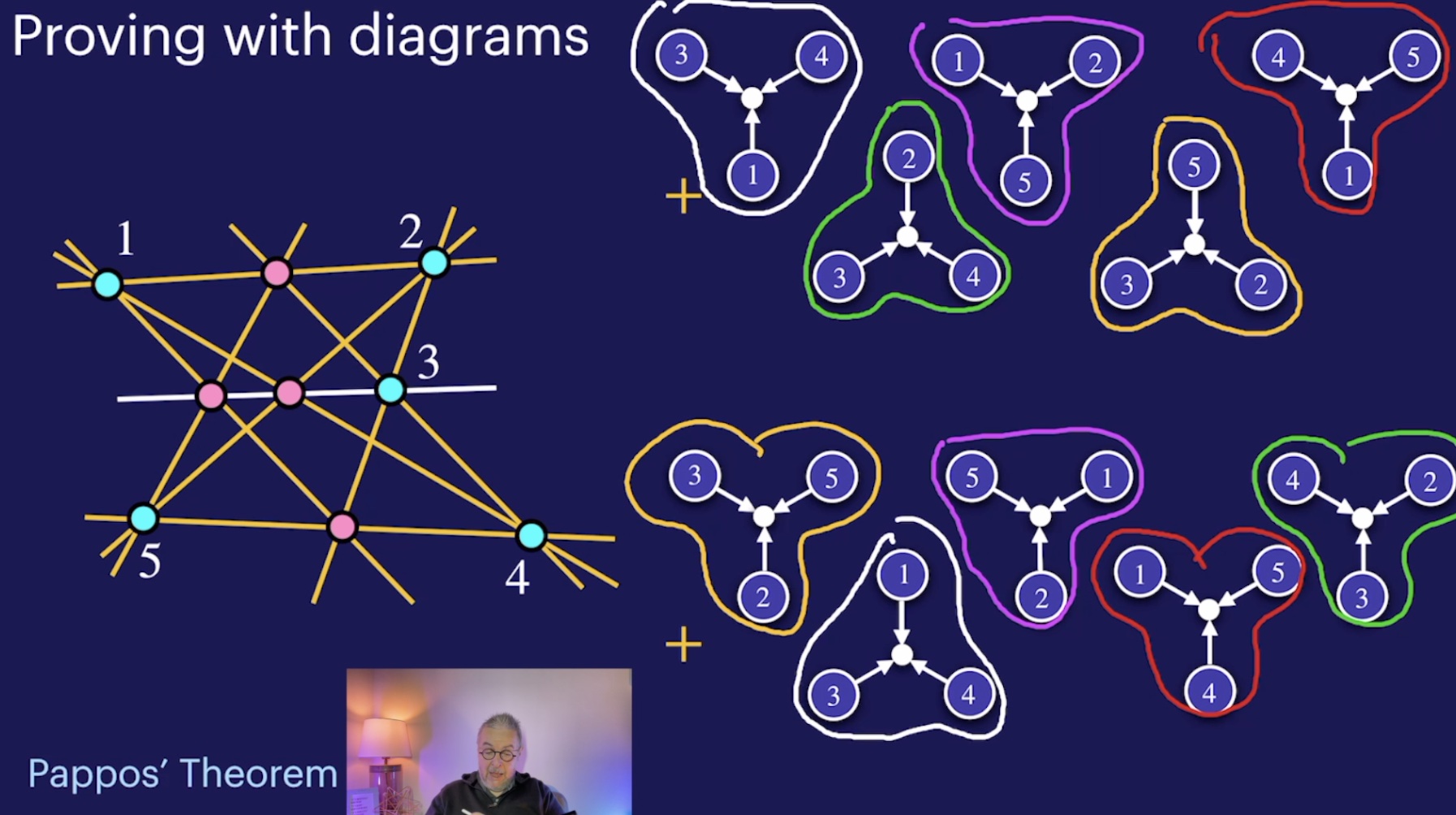
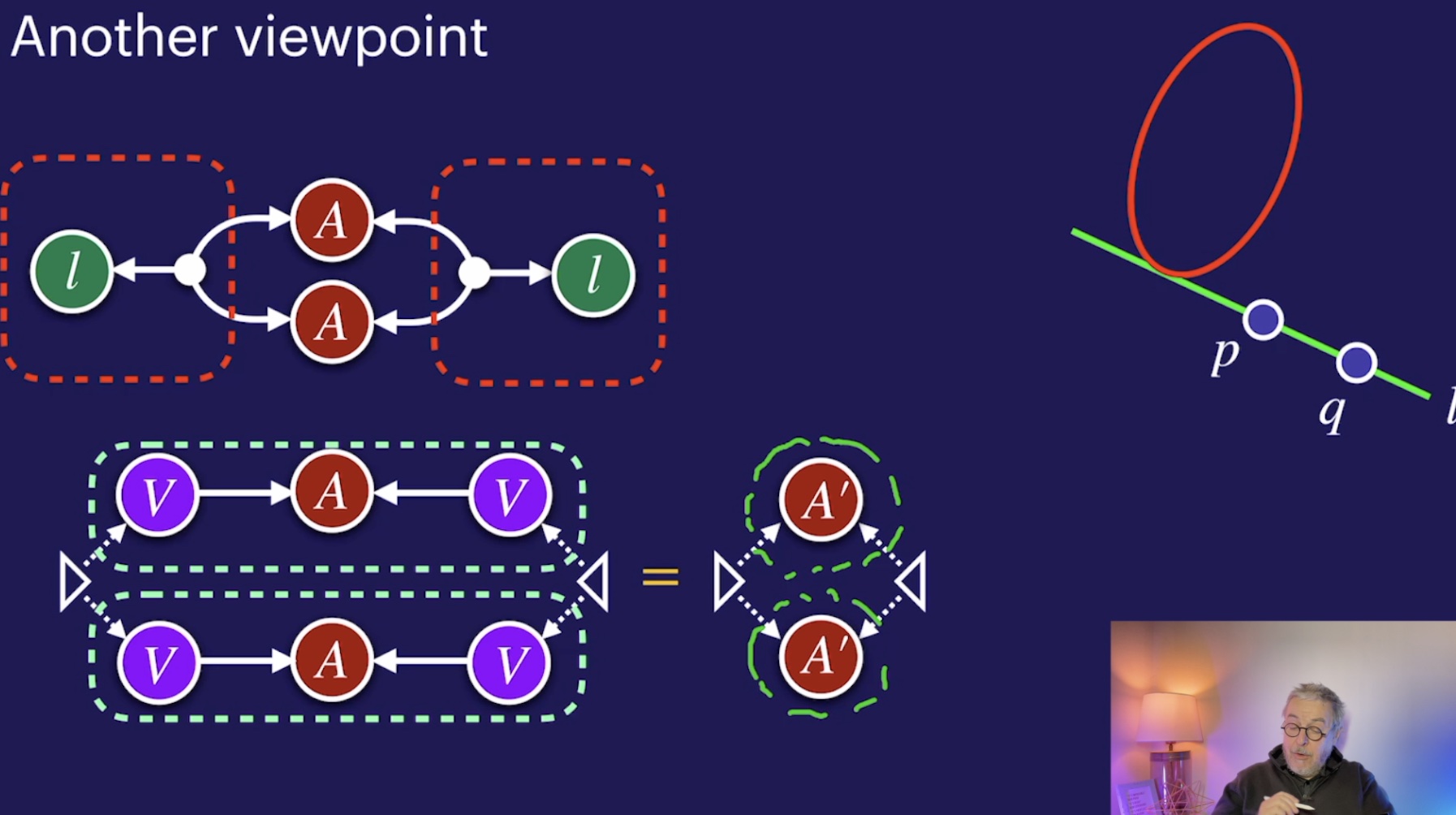
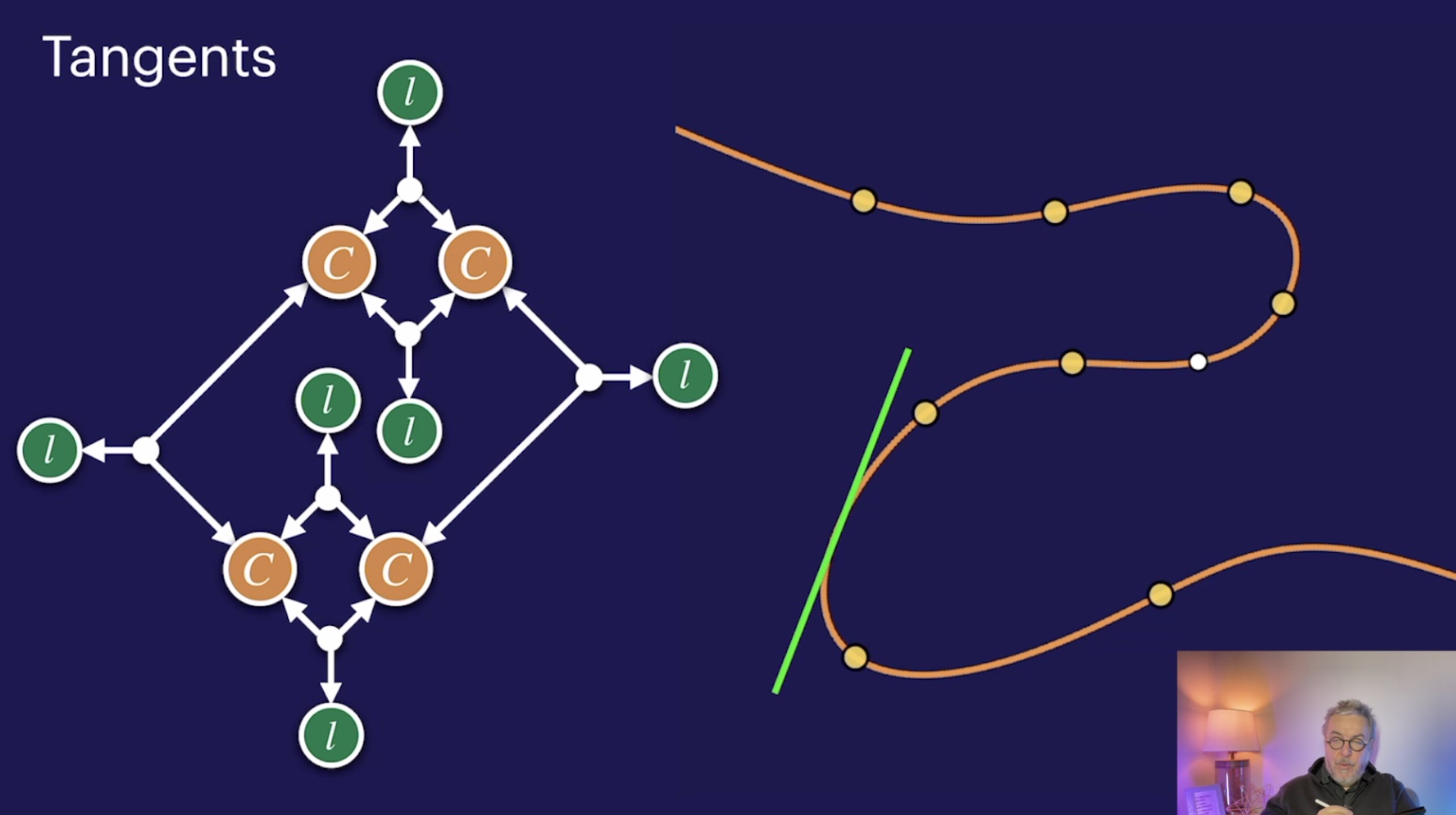
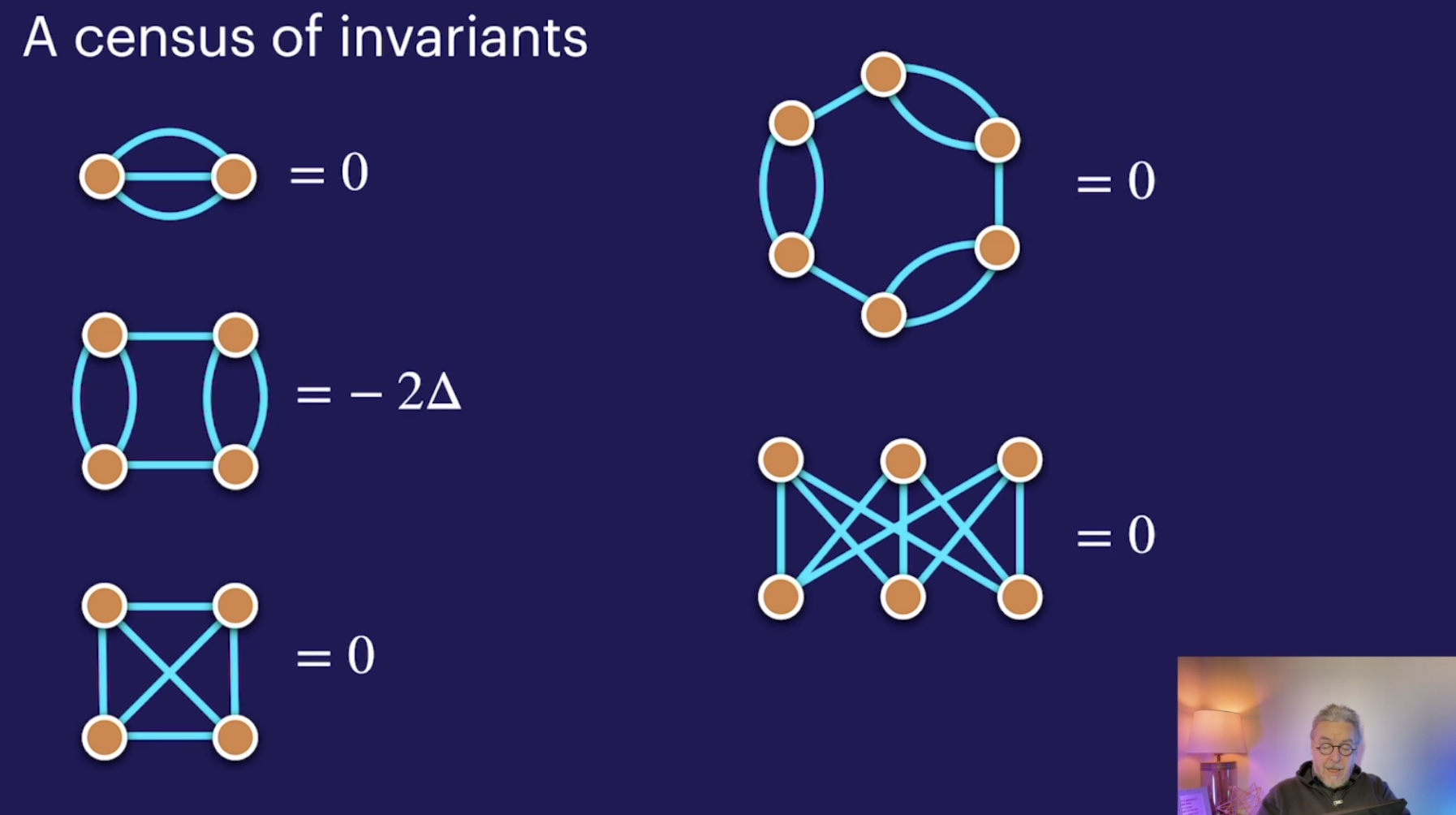
Diagrams and incidence theorems (44:47)
Conics and cubics: Basic concepts (28:45)
Discriminants of conics and cubics (56:12)
Small tensor diagrams (34:24)



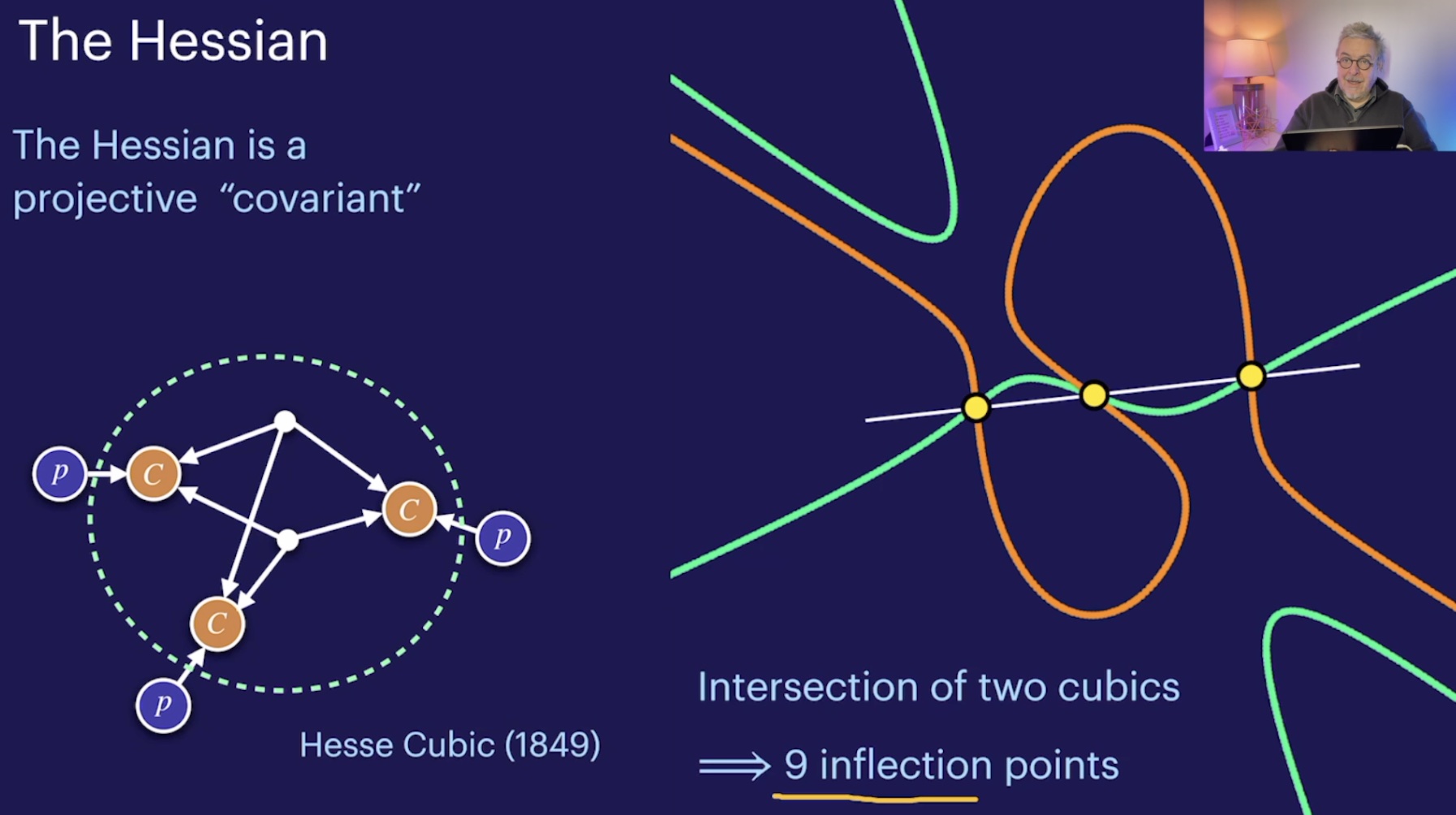
Cubics with prescribed properties (50:21)
Projective theory of cubic curves (52:58)
Discriminants and invariants of a cubic curve (20:38)
The Hessian of a cubic (54:46)